19.1 – Volatility Types
The last few chapters have laid a foundation of sorts to help us understand Volatility better. We now know what it means, how to calculate the same, and use the volatility information for building trading strategies. It is now time to steer back to the main topic – Option Greek and in particular the 4th Option Greek “Vega”. Before we start digging deeper into Vega, we have to discuss one important topic – Quentin Tarantino ☺.
I’m huge fan of Quentin Tarantino and his movies. For people not familiar with Quentin Tarantino let me tell you, he is one of the most talented directors in Hollywood. He is the man behind super cult flicks such as Pulp Fiction, Kill Bill, Reservoir Dogs, Django Unchained etc. If you’ve not watched his movies, I’d suggest you do, you may just love these movies as much as I do.
It is a known fact that when Quentin Tarantino directs a movie, he keeps all the production details under wraps until the movies trailer hits the market. Only after the trailer is out people get to know the name of movie, star cast details, brief story line, movie location etc. However, this is not the case with the movie he is directing these days, titled “The Hateful Eight”, due to be released in December 2015. Somehow everything about ‘The Hateful Eight’ – the star cast, storyline, location etc is leaked, hence people already know what to expect from Tarantino. Now given that most of the information about the movie is already known, there are wild speculations about the box office success of his upcoming movie.
We could do some analysis on this –
- Past movies – We know almost all of Tarantino’s previous movies were successful. Based on his past directorial performance we can be reasonably certain that ‘The Hateful Eight’ is likely to be a box office hit
- Movie Analyst’s forecast – There are these professional Hollywood movie analysts, who understand the business of cinema very well. Some of these analysts are forecasting that ‘The Hateful Eight’ may not do well (unlike his previous flicks) as most of the details pertaining to the movie is already, failing to enthuse the audience
- Social Media – If you look at the discussions on ‘The Hateful Eight’ on social media sites such as Twitter and Facebook, you’d realize that a lot of people are indeed excited about the movie, despite knowing what to expect from the movie. Going by the reactions on Social Media, ‘The Hateful Eight’ is likely to be a hit.
- The actual outcome – Irrespective of what really is being expected, once the movie is released we would know if the movie is a hit or a flop. Of course this is the final verdict for which we have to wait till the movie is released.
Tracking the eventual fate of the movie is not really our concern, although I’m certainly going to watch the movie ☺.
Given this, you may be wondering why we are even discussing Quentin Tarantino in a chapter concerning Options and Volatility! Well this is just my attempt (hopefully not lame) to explain the different types of volatility that exist – Historical Volatility, Forecasted Volatility, and Implied Volatility. So let’s get going.
Historical Volatility is similar to us judging the box office success of ‘The Hateful Eight’ based on Tarantino’s past directorial ventures. In the stock market world, we take the past closing prices of the stock/index and calculate the historical volatility. Do recall, we discussed the technique of calculating the historical volatility in Chapter 16. Historical volatility is very easy to calculate and helps us with most of the day to day requirements – for instance historical volatility can ‘somewhat’ be used in the options calculator to get a ‘quick and dirty’ option price (more on this in the subsequent chapters).
Forecasted Volatility is similar to the movie analyst attempting to forecast the fate of ‘The Hateful Eight’. In the stock market world, analysts forecast the volatility. Forecasting the volatility refers to the act of predicting the volatility over the desired time frame.
However, why would you need to predict the volatility? Well, there are many option strategies, the profitability of which solely depends on your expectation of volatility. If you have a view of volatility – for example you expect volatility to increase by 12.34% over the next 7 trading sessions, then you can set up option strategies which can profit this view, provided the view is right.
Also, at this stage you should realize – to make money in the stock markets it is NOT necessary to have a view on the direction on the markets. The view can be on volatility as well. Most of the professional options traders trade based on volatility and not really the market direction. I have to mention this – many traders find forecasting volatility is far more efficient than forecasting market direction.
Now clearly having a mathematical/statistical model to predict volatility is much better than arbitrarily declaring “I think the volatility is going to shoot up”. There are a few good statistical models such as ‘Generalized AutoRegressive Conditional Heteroskedasticity (GARCH) Process’. I know it sounds spooky, but that’s what it’s called. There are several GARCH processes to forecast volatility, if you are venturing into this arena, I can straightaway tell you that GARCH (1,1) or GARCH (1,2) are better suited processes for forecasting volatility.
Implied Volatility (IV) is like the people’s perception on social media. It does not matter what the historical data suggests or what the movie analyst is forecasting about ‘The Hateful Eight’. People seem to be excited about the movie, and that is an indicator of how the movie is likely to fare. Likewise the implied volatility represents the market participant’s expectation on volatility. So on one hand we have the historical and forecasted volatility, both of which are sort of ‘manufactured’ while on the other hand we have implied volatility which is in a sense ‘consensual’. Implied volatility can be thought of as consensus volatility arrived amongst all the market participants with respect to the expected amount of underlying price fluctuation over the remaining life of an option. Implied volatility is reflected in the price of the premium.
For this reason amongst the three different types of volatility, the IV is usually more valued.
You may have heard or noticed India VIX on NSE website, India VIX is the official ‘Implied Volatility’ index that one can track. India VIX is computed based on a mathematical formula, here is a whitepaper which explains how India VIX is calculated –
If you find the computation a bit overwhelming, then here is a quick wrap on what you need to know about India VIX (I have reproduced some of these points from the NSE’s whitepaper) –
- NSE computes India VIX based on the order book of Nifty Options
- The best bid-ask rates for near month and next-month Nifty options contracts are used for computation of India VIX
- India VIX indicates the investor’s perception of the market’s volatility in the near term (next 30 calendar days)
- Higher the India VIX values, higher the expected volatility and vice-versa
- When the markets are highly volatile, market tends to move steeply and during such time the volatility index tends to rise
- Volatility index declines when the markets become less volatile. Volatility indices such as India VIX are sometimes also referred to as the ‘Fear Index’, because as the volatility index rises, one should become careful, as the markets can move steeply into any direction. Investors use volatility indices to gauge the market volatility and make their investment decisions
- Volatility Index is different from a market index like NIFTY. NIFTY measures the direction of the market and is computed using the price movement of the underlying stocks whereas India VIX measures the expected volatility and is computed using the order book of the underlying NIFTY options. While Nifty is a number, India VIX is denoted as an annualized percentage
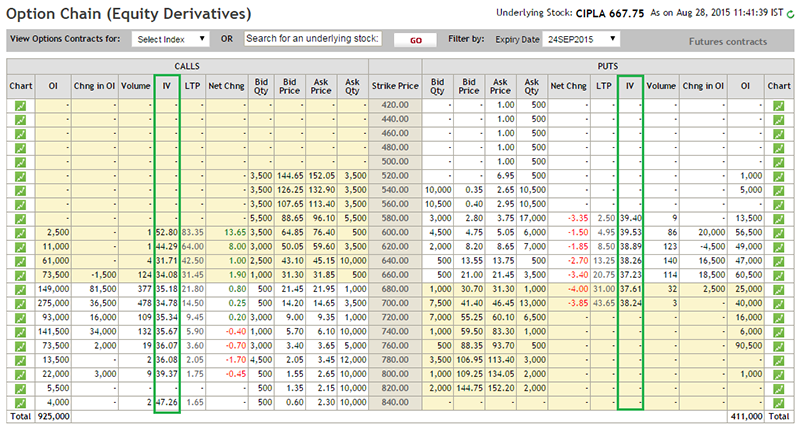
Further, NSE publishes the implied volatility for various strike prices for all the options that get traded. You can track these implied volatilities by checking the option chain. For example here is the option chain of Cipla, with all the IV’s marked out.
The Implied Volatilities can be calculated using a standard options calculator. We will discuss more about calculating IV, and using IV for setting up trades in the subsequent chapters. For now we will now move over to understand Vega.
Realized Volatility is pretty much similar to the eventual outcome of the movie, which we would get to know only after the movie is released. Likewise the realized volatility is looking back in time and figuring out the actual volatility that occurred during the expiry series. Realized volatility matters especially if you want to compare today’s implied volatility with respect to the historical implied volatility. We will explore this angle in detail when we take up “Option Trading Strategies”.

19.2 – Vega
Have you noticed this – whenever there are heavy winds and thunderstorms, the electrical voltage in your house starts fluctuating violently, and with the increase in voltage fluctuations, there is a chance of a voltage surge and therefore the electronic equipments at house may get damaged.
Similarly, when volatility increases, the stock/index price starts swinging heavily. To put this in perspective, imagine a stock is trading at Rs.100, with increase in volatility, the stock can start moving anywhere between 90 and 110. So when the stock hits 90, all PUT option writers start sweating as the Put options now stand a good chance of expiring in the money. Similarly, when the stock hits 110, all CALL option writers would start panicking as all the Call options now stand a good chance of expiring in the money.
Therefore irrespective of Calls or Puts when volatility increases, the option premiums have a higher chance to expire in the money. Now, think about this – imagine you want to write 500 CE options when the spot is trading at 475 and 10 days to expire. Clearly there is no intrinsic value but there is some time value. Hence assume the option is trading at Rs.20. Would you mind writing the option? You may write the options and pocket the premium of Rs.20/- I suppose. However, what if the volatility over the 10 day period is likely to increase – maybe election results or corporate results are scheduled at the same time. Will you still go ahead and write the option for Rs.20? Maybe not, as you know with the increase in volatility, the option can easily expire ‘in the money’ hence you may lose all the premium money you have collected. If all option writers start fearing the volatility, then what would compel them to write options? Clearly, a higher premium amount would. Therefore instead of Rs.20, if the premium was 30 or 40, you may just think about writing the option I suppose.
In fact this is exactly what goes on when volatility increases (or is expected to increase) – option writers start fearing that they could be caught writing options that can potentially transition to ‘in the money’. But nonetheless, fear too can be overcome for a price, hence option writers expect higher premiums for writing options, and therefore the premiums of call and put options go up when volatility is expected to increase.
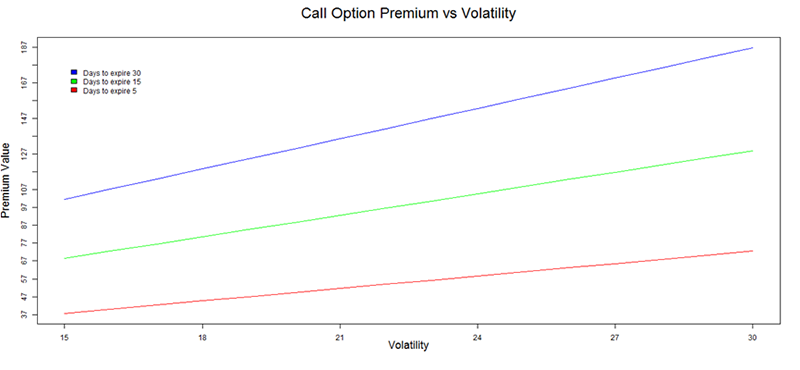
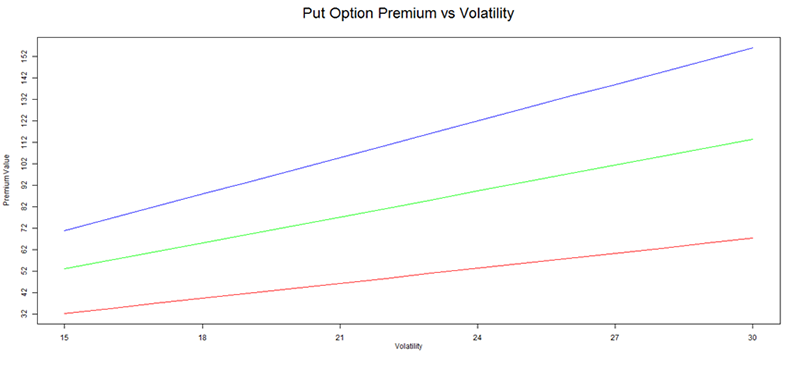
The graphs below emphasizes the same point –
X axis represents Volatility (in %) and Y axis represents the premium value in Rupees. Clearly, as we can see, when the volatility increases, the premiums also increase. This holds true for both call and put options. The graphs here go a bit further, it shows you the behavior of option premium with respect to change in volatility and the number of days to expiry.
Have a look at the first chart (CE), the blue line represents the change in premium with respect to change in volatility when there is 30 days left for expiry, likewise the green and red line represents the change in premium with respect to change in volatility when there is 15 days left and 5 days left for expiry respectively.
Keeping this in perspective, here are a few observations (observations are common for both Call and Put options) –
- Referring to the Blue line – when there are 30 days left for expiry (start of the series) and the volatility increases from 15% to 30%, the premium increases from 97 to 190, representing about 95.5% change in premium
- Referring to the Green line – when there are 15 days left for expiry (mid series) and the volatility increases from 15% to 30%, the premium increases from 67 to 100, representing about 50% change in premium
- Referring to the Red line – when there are 5 days left for expiry (towards the end of series) and the volatility increases from 15% to 30%, the premium increases from 38 to 56, representing about 47% change in premium
Keeping the above observations in perspective, we can make few deductions –
- The graphs above considers a 100% increase of volatility from 15% to 30% and its effect on the premiums. The idea is to capture and understand the behavior of increase in volatility with respect to premium and time. Please be aware that observations hold true even if the volatility moves by smaller amounts like maybe 20% or 30%, its just that the respective move in the premium will be proportional
- The effect of Increase in volatility is maximum when there are more days to expiry – this means if you are at the start of series, and the volatility is high then you know premiums are plum. Maybe a good idea to write these options and collect the premiums – invariably when volatility cools off, the premiums also cool off and you could pocket the differential in premium
- When there are few days to expiry and the volatility shoots up the premiums also goes up, but not as much as it would when there are more days left for expiry. So if you are a wondering why your long options are not working favorably in a highly volatile environment, make sure you look at the time to expiry
So at this point one thing is clear – with increase in volatility, the premiums increase, but the question is ‘by how much?’. This is exactly what the Vega tells us.
The Vega of an option measures the rate of change of option’s value (premium) with every percentage change in volatility. Since options gain value with increase in volatility, the vega is a positive number, for both calls and puts. For example – if the option has a vega of 0.15, then for each % change in volatility, the option will gain or lose 0.15 in its theoretical value.
19.3 – Taking things forward
It is now perhaps time to revisit the path this module on Option Trading has taken and will take going forward (over the next few chapters).
We started with the basic understanding of the options structure and then proceeded to understand the Call and Put options from both the buyer and sellers perspective. We then moved forward to understand the moneyness of options and few basic technicalities with respect to options.
We further understood option Greeks such as the Delta, Gamma, Theta, and Vega along with a mini series of Normal Distribution and Volatility.
At this stage, our understanding on Greeks is one dimensional. For example we know that as and when the market moves the option premiums move owing to delta. But in reality, there are several factors that works simultaneously – on one hand we can have the markets moving heavily, at the same time volatility could be going crazy, liquidity of the options getting sucked in and out, and all of this while the clock keeps ticking. In fact this is exactly what happens on an everyday basis in markets. This can be a bit overwhelming for newbie traders. It can be so overwhelming that they quickly rebrand the markets as ‘Casino’. So the next time you hear someone say such a thing about the markets, make sure you point them to Varsity ☺.
Anyway, the point that I wanted to make is that all these Greeks manifest itself on the premiums and therefore the premiums vary on a second by second basis. So it becomes extremely important for the trader to fully understand these ‘inter Greek’ interactions of sorts. This is exactly what we will do in the next chapter. We will also have a basic understanding of the Black & Scholes options pricing formula and how to use the same.
19.4 – Flavors of Inter Greek Interactions
(The following article was featured in Business Line dated 31st August 2015)
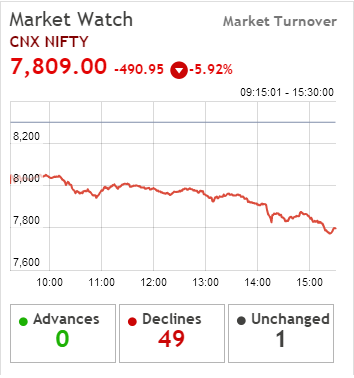
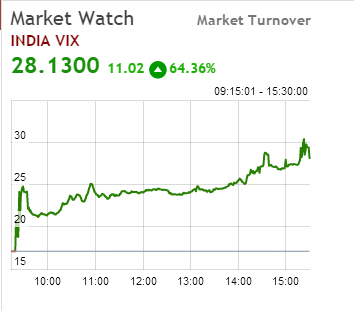
Here is something that happened very recently. By now everyone remotely connected with the stock market would know that on 24th August 2015, the Indian markets declined close to 5.92% making it one of the worse single day declines in the history of Indian stock markets. None of the front line stocks survived the onslaught and they all declined by 8-10%. Panic days such as these are a common occurrence in the equity markets.
However something unusual happened in the options markets on 24th August 2015, here are some data points from that day –
Nifty declined by 4.92% or about 490 points –
India VIX shot up by 64% –
But Call option Premiums shot up!
Traders familiar with options would know that the call option premiums decline when market declines. In fact most of the call option premiums (strikes below 8600) did decline in value but option strikes above 8650 behaved differently – their premium as opposed to the general expectation did not decline, rather increased by 50-80%. This move has perplexed many traders, with many of the traders attributing this move to random theories such as rate rigging, market manipulation, technological inefficiency, liquidity issues etc. But I suspect any of this is true; in fact this can be explained based on the option theory logic.
We know that option premiums are influenced by sensitivity factors aka the Option Greeks. Delta as we know captures the sensitivity of options premium with respect to the movement of the underlying. Here is a quick recap – if the Delta of a particular call option is 0.75, then for every 1 point increase/decrease in the underlying the premium is expected to increase/decrease by 0.75 points. On 24th August, Nifty declined by 490 points, so all call options which had ‘noticeable Delta’ (like 0.2, 0.3, 0.6 etc) declined. Typically ‘in the money’ options (as on 24th Aug, all strike below 8600) tend to have noticeable Delta, therefore all their premiums declined with the decline in the underlying.
‘Out of the money’ options usually have a very low delta like 0.1 or lower. This means, irrespective of the move in the underlying the moment in the option premium will be very restrictive. As on August 24th, all options above 8600 were ‘out of the money’ options with low delta values. Hence irrespective of the massive fall in the market, these call options did not lose much premium value.
The above explains why certain call options did not lose value, but why did the premiums go up? The answer to this is lies in Vega – the option Greek which captures the sensitivity of market volatility on options premiums.
With increase in volatility, the Vega of an option increases (irrespective of calls and puts), and with increase in Vega, the option premium tends to increase. On 24th August the volatility of Indian markets shot up by 64%. This increase in volatility was totally unexpected by the market participants. With the increase in volatility, the Vega of all options increases, thereby their respective premiums also increased. The effect of Vega is particularly high for ‘Out of the money’ options. So on one hand the low delta value of ‘out of the money’ call options prevented the option premiums from declining while on the other hand, high Vega value increased the option premium for these out of the money options.
Hence on 24th August 2015 we got to witness the unusual – call option premium increasing 50 – 80% on a day when markets crashed 5.92%.
Key takeaways from this chapter
- Historical Volatility is measured by the closing prices of the stock/index
- Forecasted Volatility is forecasted by volatility forecasting models
- Implied Volatility represents the market participants expectation of volatility
- India VIX represents the implied volatility over the next 30 days period
- Vega measures the rate of change of premium with respect to change in volatility
- All options increase in premium when volatility increases
- The effect of volatility is highest when there are more days left for expiry


Do you plan to have a module/chapter on mathematical/statistical models in trading?
On the same note, do you use VAR,GARCH,ARIMA etc. and different time series models using a forecasting software like EVIEWS for trading.
Is it a good idea to combine statistical models with technical analysis for trading or are they chalk and cheese?
Rajdeep – a module on Statistical models will be an awesome! Will probably do that sometime in future.
Yes, I’ve used GARCH models earlier…but these were built from scratch on R and Excel. Have not used any software for this. Also, I’m not sure if its a good idea to combine TA and stats…never done that before so cant really comment.
Does Vega won’t have negative value
Nope.
Dear Karthik,
Today, for the 1st time, I made a profit of more than Rs.1000/- on Zerodha website since I am client of Zerodha client. Previously, I mistakenly made a loss of Rs. 270/-. The full credit for this goes to u, because of u I was able to understand options very well. God bless and continue this valuable service to us and the society in whole.
I’m so glad to hear this, hope this is the start of something bigger for you. By the way you need to attribute your success to your hard work and nothing else 🙂
Good luck!
Awesomeness !!!! Wish I had read this before 16th May 2014 the election results day, I was long and in handsome virtual profit but suddenly the market went down (now I know the volatility dried up) :-).
I wish vega of brining the newer lessons go high and we don’t have to wait long for next chapter . 🙂
The beauty of markets is that there are always opportunities….it upto you to figure out where it lies!
Will try our best to upload chapter soon 🙂
very true W.R.T markets opportunities knocks everyday 🙂
Thanks again for your hard and wonderful work.
Stay profitable!
hi Karthik, so what does a vega of say 12 and the price of a particular underlying moving by INR 10 signify?
Raj – thanks for bringing this point. I seem to have missed this concept all together. I will work on this this right away…
could not get it.
Vega corresponds to which volatility?
Implied Volatility.
hi karthik, awaiting your views on the above query i had raised. was keenly expecting it to be addressed in the recent module. thanks.
My query was: so what does a vega of say 12 and the price of a particular underlying moving by INR 10 signify?
Raj – I did update section 19.2. You will find the answer towards the end of the section..please do check. Thanks.
Dear Karthik,
Can u please let me know the website wherein we can see the candlestick formation as the market is on. It was somewhere during the Options module or Technical analysis module. Can u please let me know. Regards.
Have you seen chartink.com ?