14.1 – Time is money
Remember the adage “Time is money”, it seems like this adage about time is highly relevant when it comes to options trading. Forget all the Greek talk for now, we shall go back to understand one basic concept concerning time. Assume you have enrolled for a competitive exam, you are inherently a bright candidate and have the capability to clear the exam, however, if you do not give it sufficient time and brush up the concepts, you are likely to flunk the exam – so given this what is the likelihood that you will pass this exam? Well, it depends on how much time you spend to prepare for the exam right? Let’s keep this in perspective and figure out the likelihood of passing the exam against the time spent preparing for the exam.
| Number of days for preparation | Likelihood of passing |
|---|---|
| 30 days | Very high |
| 20 days | High |
| 15 days | Moderate |
| 10 days | Low |
| 5 days | Very low |
| 1 day | Ultra-low |
Quite obviously higher the number of days for preparation, the higher is the likelihood of passing the exam. Keeping the same logic in mind, think about the following situation – Nifty Spot is 8500, you buy a Nifty 8700 Call option – what is the likelihood of this call option to expire In the Money (ITM)? Let me rephrase this question in the following way –
- Given Nifty is at 8500 today, what is the likelihood of Nifty moving 200 points over the next 30 days and therefore 8700 CE expiring ITM?
- The chance for Nifty to move 200 points over the next 30 days is quite high, hence the likelihood of an option expiring ITM upon expiry is very high
- What if there are only 15 days to expiry?
- An expectation that Nifty will move 200 points over the next 15 days is reasonable, hence the likelihood of an option expiring ITM upon expiry is high (notice it is not very high, but just high).
- What if there are only 5 days to expiry?
- Well, 5 days, 200 points, not really sure hence the likelihood of 8700 CE expiring in the money is low
- What if there was only 1 day to expiry?
- The probability of Nifty to move 200 points in 1 day is quite low, hence I would be reasonably certain that the option will not expire in the money, therefore the chance is ultra-low.
Is there anything that we can infer from the above? Clearly, the more time for expiry the likelihood for the option to expire In the Money (ITM) is higher. Now keep this point in the back of your mind as we now shift our focus on the ‘Option Seller’. We know an option seller sells/writes an option and receives the premium for it. When he sells an option he is very well aware that he carries an unlimited risk and limited reward potential. The reward is limited to the extent of the premium he receives. He gets to keep his reward (premium) fully only if the option expires worthless. Now, think about this – if he is selling an option early in the month he very clearly knows the following –
- He knows he carries unlimited risk and limited reward potential
- He also knows that by virtue of time, there is a chance for the option he is selling to transition into ITM option, which means he will not get to retain his reward (premium received)
In fact at any given point, thanks to ‘time’, there is always a chance for the option to expire in the money (although this chance gets lower and lower as time progresses towards the expiry date). Given this, an option seller would not want to sell options at all right? After all, why would you want to sell options when you very well know that simply because of time there is scope for the option you are selling to expire in the money. Clearly, time in the option sellers context acts as a risk. Now, what if the option buyer in order to entice the option seller to sell options offers to compensate for the ‘time risk’ that he (option seller) assumes? In such a case it probably makes sense to evaluate the time risk versus the compensation and take a call right? In fact, this is what happens in real-world options trading. Whenever you pay a premium for options, you are indeed paying towards –
- Time Risk
- The intrinsic value of options.
In other words – Premium = Time value + Intrinsic Value Recall earlier in this module we defined ‘Intrinsic Value’ as the money you are to receive if you were to exercise your option today. Just to refresh your memory, let us calculate the intrinsic value for the following options assuming Nifty is at 8423 –
- 8350 CE
- 8450 CE
- 8400 PE
- 8450 PE
We know the intrinsic value is always a positive value or zero and can never be below zero. If the value turns out to be negative, then the intrinsic value is considered zero. We know for Call options the intrinsic value is “Spot Price – Strike Price” and for Put options, it is “Strike Price – Spot Price”. Hence the intrinsic values for the above options are as follows –
- 8350 CE = 8423 – 8350 = +73
- 8450 CE = 8423 – 8450 = -ve value hence 0
- 8400 PE = 8400 – 8423 = -ve value hence 0
- 8450 PE = 8450 – 8423 = + 27
So given that we know how to calculate the intrinsic value of an option, let us attempt to decompose the premium and extract the time value and intrinsic value. Have a look at the following snapshot – 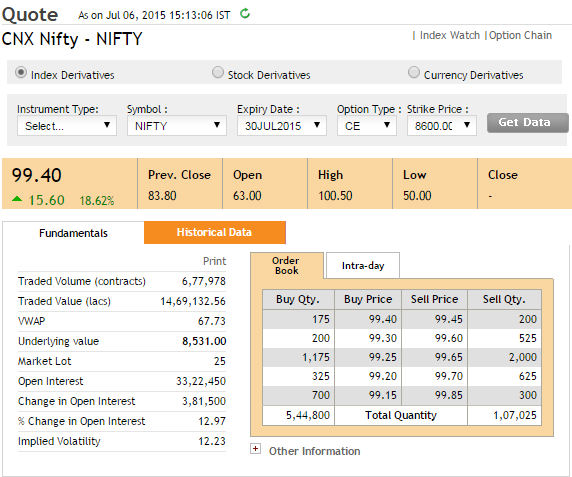 Details to note are as follows –
Details to note are as follows –
- Spot Value = 8531
- Strike = 8600 CE
- Status = OTM
- Premium = 99.4
- Today’s date = 6th July 2015
- Expiry = 30th July 2015
Intrinsic value of a call option – Spot Price – Strike Price i.e 8531 – 8600 = 0 (since it’s a negative value) We know – Premium = Time value + Intrinsic value 99.4 = Time Value + 0 This implies Time value = 99.4! Do you see that? The market is willing to pay a premium of Rs.99.4/- for an option that has zero intrinsic value but ample time value! Recall time is money ☺ Here is a snapshot of the same contract that I took the next day i.e 7th July – 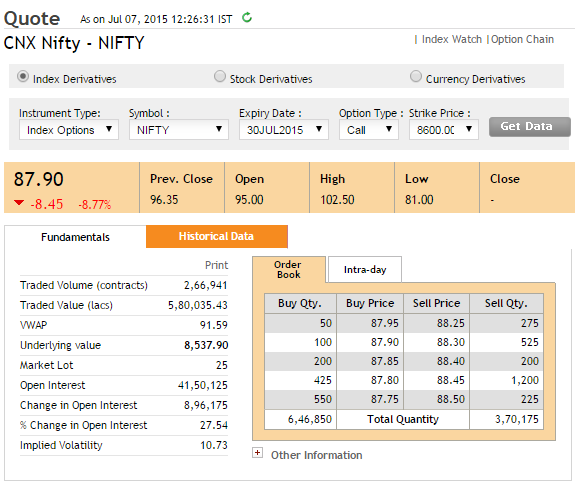 Notice the underlying value has gone up slightly (8538) but the option premium has decreased quite a bit! Let’s decompose the premium into its intrinsic value and time value – Spot Price – Strike Price i.e 8538 – 8600 = 0 (since it’s a negative value) We know – Premium = Time value + Intrinsic value 87.9 = Time Value + 0 This implies Time value = 87.9! Notice the overnight drop in premium value? We will soon understand why this happened. Note – In this example, the drop in premium value is 99.4 minus 87.9 = 11.5. This drop is attributable to a drop in volatility and time. We will talk about volatility in the next chapter. For the sake of argument, if both volatility and spot were constant, the drop in premium would be completely attributable to the passage of time. I would suspect this drop would be around Rs.5 or so and not really Rs.11.5/-. Let us take another example –
Notice the underlying value has gone up slightly (8538) but the option premium has decreased quite a bit! Let’s decompose the premium into its intrinsic value and time value – Spot Price – Strike Price i.e 8538 – 8600 = 0 (since it’s a negative value) We know – Premium = Time value + Intrinsic value 87.9 = Time Value + 0 This implies Time value = 87.9! Notice the overnight drop in premium value? We will soon understand why this happened. Note – In this example, the drop in premium value is 99.4 minus 87.9 = 11.5. This drop is attributable to a drop in volatility and time. We will talk about volatility in the next chapter. For the sake of argument, if both volatility and spot were constant, the drop in premium would be completely attributable to the passage of time. I would suspect this drop would be around Rs.5 or so and not really Rs.11.5/-. Let us take another example – 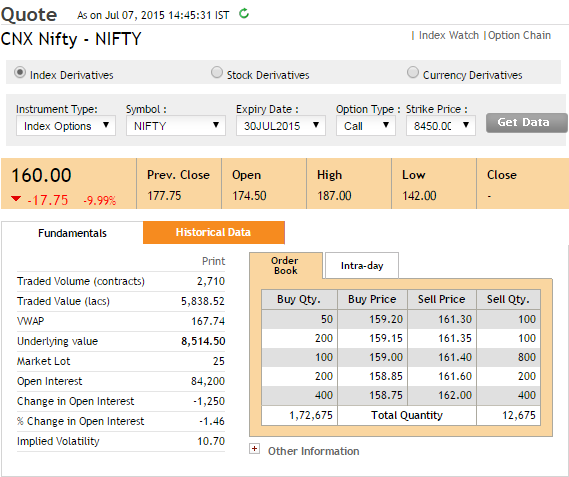
- Spot Value = 8514.5
- Strike = 8450 CE
- Status = ITM
- Premium = 160
- Today’s date = 7th July 2015
- Expiry = 30th July 2015
Intrinsic value of call option – Spot Price – Strike Price i.e 8514.5 – 8450 = 64.5 We know – Premium = Time value + Intrinsic value 160 = Time Value + 64.5 This implies the Time value = 160 – 64.5 = 95.5 Hence out of the total premium of Rs.160, traders are paying 64.5 towards intrinsic value and 95.5 towards the time value. You can repeat the calculation for all options (both calls and puts) and decompose the premium into the Time value and intrinsic value.
14.2 – Movement of time
Time as we know moves in one direction. Keep the expiry date as the target time and think about the movement of time. Quite obviously as time progresses, the number of days for expiry gets lesser and lesser. Given this let me ask you this question – With roughly 18 trading days to expiry, traders are willing to pay as much as Rs.100/- towards time value, will they do the same if the time to expiry was just 5 days? Obviously, they would not right? With lesser time to expiry, traders will pay a much lesser value towards time. In fact here is a snapshot that I took from the earlier months – 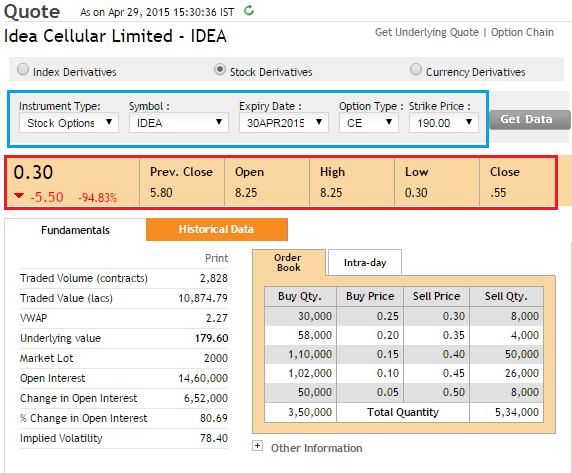
- Date = 29th April
- Expiry Date = 30th April
- Time to expiry = 1 day
- Strike = 190
- Spot = 179.6
- Premium = 30 Paisa
- Intrinsic Value = 179.6 – 190 = 0 since it’s a negative value
- Hence time value should be 30 paisa which equals the premium
With 1 day to expiry, traders are willing to pay a time value of just 30 paise. However, if the time to expiry was 20 days or more the time value would probably be Rs.5 or Rs.8/-. The point that I’m trying to make here is this – with every passing day, as we get closer to the expiry day, the time to expiry becomes lesser and lesser. This means the option buyers will pay lesser and lesser towards time value. So if the option buyer pays Rs.10 as the time value today, tomorrow he would probably pay Rs.9.5/- as the time value. This leads us to a very important conclusion – “All other things being equal, an option is a depreciating asset. The option’s premium erodes daily and this is attributable to the passage of time”. Now the next logical question is – by how much would the premium decrease on a daily basis owing to the passage of time? Well, Theta the 3rd Option Greek helps us answer this question. 
14.3 – Theta
All options – both Calls and Puts lose value as the expiration approaches. The Theta or time decay factor is the rate at which an option loses value as time passes. Theta is expressed in points lost per day when all other conditions remain the same. Time runs in one direction, hence theta is always a positive number, however, to remind traders it’s a loss in options value it is sometimes written as a negative number. A Theta of -0.5 indicates that the option premium will lose -0.5 points for every day that passes by. For example, if an option is trading at Rs.2.75/- with a theta of -0.05 then it will trade at Rs.2.70/- the following day (provided other things are kept constant). A long option (option buyer) will always have a negative theta meaning all else equal, the option buyer will lose money on a day by day basis. A short option (option seller) will have positive theta. Theta is a friendly Greek to the option seller. Remember the objective of the option seller is to retain the premium. Given that options lose value on a daily basis, the option seller can benefit by retaining the premium to the extent it loses value owing to time. For example, if an option writer has sold options at Rs.54, with a theta of 0.75, all else equal, the same option is likely to trade at – =0.75 * 3 = 2.25 = 54 – 2.25 = 51.75 Hence the seller can choose to close the option position on T+ 3 day by buying it back at Rs.51.75/- and profiting Rs.2.25 …and this is attributable to theta! Have a look at the graph below – 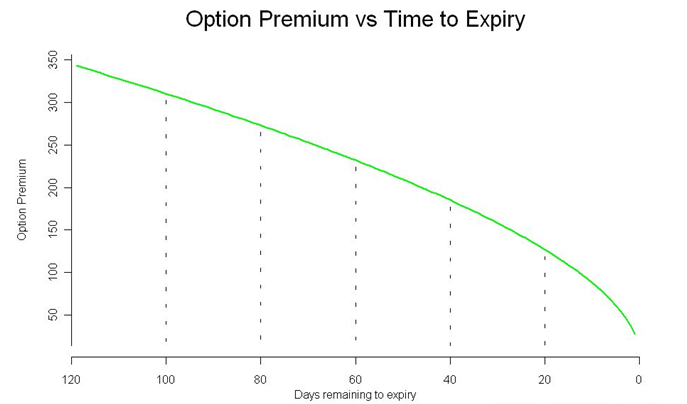 This is the graph of how premium erodes as a time to expiry approaches. This is also called the ‘Time Decay’ graph. We can observe the following from the graph –
This is the graph of how premium erodes as a time to expiry approaches. This is also called the ‘Time Decay’ graph. We can observe the following from the graph –
- At the start of the series – when there are many days for expiry, the option does not lose much value. For example, when there were 120 days to expiry the option was trading at 350, however, when there were 100 days to expiry, the option was trading at 300. Hence the effect of theta is low
- As we approach the expiry of the series – the effect of theta is high. Notice when there were 20 days to expiry the option was trading around 150, but when we approach towards expiry the drop in premium seems to accelerate (option value drops below 50).
So if you are selling options at the start of the series – you have the advantage of pocketing a large premium value (as the time value is very high) but do remember the fall in premium happens at a low rate. You can sell options closer to the expiry – you will get a lower premium but the drop in premium is high, which is advantageous to the options seller. Theta is a relatively straightforward and easy Greek to understand. We will revisit theta again when we will discuss cross dependencies of Greeks. But for now, if you have understood all that’s being discussed here you are good to go. We shall now move forward to understand the last and the most interesting Greek – Vega!
Key takeaways from this chapter
- Option sellers are always compensated for the time risk
- Premium = Intrinsic Value + Time Value
- All else equal, options lose money on a daily basis owing to Theta
- Time moves in a single direction hence Theta is a positive number
- Theta is a friendly Greek to option sellers
- When you short naked options at the start of the series you can pocket a large time value but the fall in premium owing to time is low
- When you short option close to expiry the premium is low (thanks to time value) but the fall in premium is rapid


Does theya decay affect ITM, ATM & OTM options differently for the same underlying?
Yes, the acceleration is higher for OTM and ATM options as we approach expiry. Its lesser for ITM and deep ITM options.
I meant; I tried all four combinations.
actual spot, Sensibull based IV
actual spot, NSE website based IV
Nifty Mar Fut, Sensibull based IV
Nifty Mar Fut, NSE website based IV
I tried
Spot=Nifty Mar Fut
& NSE website based IV( Last time I used Sensibull based IV. ).
Unfortunately problem persists.☹
Am I doing anything wrong?
Ah no, it could be some mismatch in input variables. Please do talk to Sensibull customer desk.
1) My query was about FORMATTING.
2) If call option value depreciates by 1.259 every day, then same will be CLOSE to 0 within 13.5÷1.259=10.72 days; however expiry is 23 days( including 5th n 27th March ) away.
hmm, got it. I need to find out as well. Ideally the theta decay to zero should coincide with the expiry. I\’m sure both of us are missing something obvious 🙂
Hi Karthik,
For
Spot=22000
Strike=23500
Expiry=2025-03-27 15:30:00
Volatility=13.4
Interest=6.44
Dividend=0
I got
Call Option Premium=8.54( Actual value is 13.50 )
Call Option Theta=-1.259( in Red )
Put Option Theta=2.871( in Green )
Can you please confirm;
1) has Call Option Theta value been formatted from option buyer\’s perspective & Put Option Theta value from option seller\’s perspective?
2) is given Call Option Theta value reliable if we consider ACTUAL Call Option Premium & Expiry?
Thank you.
1) Theta is not specific to either the buyer or seller. Its from the strike\’s perspective
2) Yes it should be. Why do you think it wont be?
Thanks for the article sir , it is very helpful for the new traders.
I just want to confirm that which trade is more profitable to option buyers , Is it ITM, OTM or ATM , if the market is little bullish or neutral.
There is no one trade the benefits everytime. You really need to understand the market and the situation in the market and deploy a trade that has better odds of working in your favor.
Hey Karthik I know I am a bit late for queries but while writing CE if we\’re gonna buy back the options at the closer date to expiry how are we gonna exit from this trade as I want to avoid physical settlement?
When you close, you get out of the trade completely. You no longer have an open position.
But currently, if i see, the strike prices that have long gone has higher LTP. Does it mean, if i buy a strike price after 90 days, and by the time if that respective strike price crosses the spot price, the premium keeps on increasing to certain value?
Yes, the deeper the strikes becomes ITM, the higher the premium.
How can I determine, when(time) the option reach the predicted target on intraday?
That is a hard call, Gopinath. Not sure if its possible to establish it 🙂
Can you please make a video series for NISM Series VIII – Equity and derivative exam. Your videos are really helpfull!
We have put up a lot of videos here – https://www.youtube.com/@varsitybyzerodha
plese keep varsity up to date…
it is very helpfull…
thanks
These concepts dont really change, Jay. But yes, will try and update as and when required.
Hello Karthik,
Could you tell me that whether theta erodes second by second during markets hours or it erodes its value day after day. For example if theta of 22500 strike is 30 and premium is 150, then theta value drops every second given the other factors remains stable or premium will drop by 30rs next day.
I am bit confused about this.
Thanks in advance.
Theta works on a continuous basis, but at the same time there are other greeks working on premiums too. The effect of theta is enhanced towards the expiry and sort of works as a dominant greek.
Hey Karthik,
I have just asked Gemini to go to Zerodha Versity\’s Theta chapter and give me some answer:
Question (me): Can you tell me relation between theta and different strike?
Answer (Gemini) :
\”Imagine Theta as a rate of ice melting. A larger ice cube (higher strike price, OTM option) melts slower than a smaller ice cube (lower strike price, ITM option) because it has less initial volume to lose. However, a flat sheet of ice (ATM option) with a larger surface area might melt the fastest due to having the most exposed area for heat transfer (time decay).\”
AI is Amazing, isn\’t it?
AI is amazing, but this example, I\’m not sure 🙂
It could be right or wrong depending on call or put 🙂
Sir,
Please consider the below two scenarios, considering Expiry=30th Jul,2015-
Day 1 (6th Jul,2015):
Strike=8600 CE
Spot Value=8531
Premium=99.4
We know premium= Time value+Intrinsic value
Intrinsic value=0
So, time value=99.4
Day 2 (7th Jul,2015):
Strike=8600 CE
Spot Value=8510
Premium=94
Intrinsic value=0
So, time value=94
Please assure if I am correct with the below statement-
From the above two situations, and through the equation, premium= Time value+Intrinsic value, we understood that although the spot price drops but the drop in premium is attributable to only Theta. However, since the price is dropping this premium dropping should also come from drop in Delta (Due to Gamma) and due to Delta. Am I correct? I am ignoring the effect of Volatility for the time being.
You cant really ignore the effect of volatility 🙂
The effect of option premium is an outcome of all these greeks.
For deep ORM options, the premium value is low. Right? Even though we get a buyer (for Nifty or Bank Nifty) the returns might be low. Is this correct understanding?
Hmm, yes premiums are low for OTM options, but returns being low is subjective 🙂
It is possible if I carry Iron Butterfly for overnight. I deploy it at 3:15PM on Wednesday and exit at 9:16AM on Thursday. And hypothetically if market remain at the same price. Do I make profit?
Sure, you can. In fact, its best if you plan your trade in such a way that it can be carried out and held to expiry.
Does most of the theta decay happens overnight? Because I\’m playing with short straddle strategies in sensibull. App showing me total one day decay of 2048 rupees. But when I changed time frame to 3:15PM to see what my P&L would be ( if spot & IV is unchanged. ) It was just 448 rupees.But when I changed time to 9:15AM of next day my p&l become 2048. Does that mean large chunk of theta decay happens overnight?
It feels like that, but theta decay happens with the passage of time 🙂
Hi, Karthik Sir, I have a question about Weekly Calendar Spreads. Here is some data of today\’s date (16 Jan 2024) that contextualizes my query:
Put Calendar Spread:
Sell: 1x 25JAN2024 22000PE – ₹166
(Put IV: 13.02)
Buy: 1x 01FEB2024 22000PE – ₹219.6
(Put IV: 13.59)
Positional Greeks:
Delta: 1.91
Theta: 274.99
Gamma: -0.02
Vega: 454.25
Probability and Profit/Loss Metrics:
Prob. of Profit: 44.35%
Max. Profit: ₹ +5,238 (20.33%)
Max. Loss: ₹ -3,353 (-13.01%)
Max. RR Ratio: 1:1.56
Breakevens: ₹21,732.0 – ₹22,303.0
Estimated Margin/Premium: ₹ +25,763
Call Calendar Spread:
Sell: 1x 25JAN2024 22000CE – ₹188
(Call IV:12.74)
Buy: 1x 01FEB2024 22000CE – ₹295.9
(Call IV: 14.38)
Positional Greeks:
Delta: 1.58
Theta: 148.51
Gamma: -0.03
Vega: 455.59
Probability and Profit/Loss Metrics:
Prob. of Profit: 27.98%
Max. Profit: ₹ +3,664 (15.19%)
Max. Loss: ₹ -5,395 (-22.37%)
Max. RR Ratio: 1:0.68
Breakevens: ₹21,834.0 – ₹22,182.0
Estimated Margin/Premium: ₹ +24,118
My Questions:
1. Why Theta is more in Put Calendar Spread, although IVs do not have so much of a difference and DTE is the same for both.
2. Generally, I have seen that when I design put calendar spread, it shows better Breakevens and Max Profit-Loss Ratios. How does this happen?
Please explain.
1) I need to investigate this as well, but my guess is the put call parity is at play here.
2) Perhapse the puts have more premiums. Generally fear comes at a higher price 🙂
CAN WE SEE MONTHLY GRAPH / CHART OR TABLE FOR BANKNIFTY
Yes, change the frequency from daily to Monthly and you have it.
Considering volatility has no changes in intraday time frame,
why is delta even active for an OTM option if it only has none other than a depreciating time value?
I cannot understand the logic behind an OTM option having a fluctuating value (other than decrease in Theta).
Please recfity what I am missing to understand.
PS: I have read this whole module.
With the change in prices, volatility too changes every second.
Hi Karthik!
In the above, you said that the intrinsic value of an OTM option is zero. In the previous chapters of delta, we learned for OTM option delta is in btw 0.05 to 0.2 and the premium increases by this factor while the spot is moving in the positive direction for that option. My question is what do we call the increase in premium value while the spot price turns OTM option into almost ATM status but remains just short of the strike price ? Is that intrinsic value (considering the option is still OTM)?
If the intrinsic value is greater than zero only when the spot is above the strike price(for in case of CE), should not the premiums start moving only when the strike price is in ATM status?
That value can be largely attributed to time value of option as there is no intrinsic option value. Option moves due to other factors that influence option premiums, mainly volatility.
Will the theta decay continue if the stock goes in the ban list due to high traded volumes?
Yup, thats right.
Hi , so for a option buyer is it okay to buy in delivery?
Yes, you can hold options for overnight delivery as well.
Sir uper jisne bhi primium k uper swal puche mujhe kuch nhi aaya Mera swal intraday pr nahi h Mai premium ko hold karna chahta hu poore month us pr swal h
Sir agar Mai strike price ka primium buy karta hu aur nifty meri direction me move kre pura month to kya mera primium theta ki wajah se zero hoga ya expiry Wale din mujhe pura profit milega aur us pr time decay or theta ka koi frk nhi pdega sir please give response soon e-mail pr response Krna kyoki e mail roj dekhte hai yaha dobara kb dekhu pta nhi
Premium = Time value + Intrinsic value 87.9 = Time Value + 0
What is Intrinsic value 87.9 Why 87.9 is with Intrinsic value
87.9 is the premium What we Paid ?
Please Breakdown this
Premium = Time value + Intresic value
If the premium = 87.9 and the intrinsic value of an option is 0, then the entire premium can be attributed to the intrinsic value of an option.
Sir in the months of July I used to sell OTM options on every expiry. Let assume if Banknifty is on 46000 then I used to sell 46200 CE at 1:45 so if market stays lower then 46200 I used to get all the money as it becomes 0.. in July I used to get it on price between 30 to 45 but later on I only used to get on on 6 to 7 RS at the same time only on 1:45…. Can you explain this?
Premiums are a function of many factors including Volatility. Maybe the volatility has dropped on these contracts? Also it depends on how many days to expiry.
hi sir ,
Sir if we buy an otm call option with weekly expiry , suppose 6 days to expiry , with option premium being 48 and theta being -8 , so if we reach till only one day remaining to expiry , with no change in asset price as well as volatility , so will the option premium lose 8 rs ( aka theta -8 ) every day from day 6 to day 1 , or will the theta gradually increase from day 6 to day 1 ( from -8 to approx lets say -28 on the last day ) . if taken options contract for 1 week aka weekly expiry does theta decay remains constant for each day or does it increase as we approach last day . thanks a lot sir .
The option will lose money, but the premium will erode quickly on the day of the expiry.
Dear Karthik,
I have gone through this module and learned a fair understanding of the option and it\’s pricing. but here what\’s NSE is tell about pricing of derivative (NIFTY 50 F&O):
Excerpt from https://www.nseindia.com/products-services/equity-derivatives-nifty50
\”
Base Prices
Base price of the options contracts, on introduction of new contracts, would be the theoretical value of the options contract arrived at based on Black-Scholes model of calculation of options premiums.
The options price for a Call, computed as per the following Black Scholes formula:
C = S * N (d1) – X * e- rt * N (d2)
and the price for a Put is : P = X * e- rt * N (-d2) – S * N (-d1)
where :
d1 = [ln (S / X) + (r + σ2 / 2) * t] / σ * sqrt(t)
d2 = [ln (S / X) + (r – σ2 / 2) * t] / σ * sqrt(t)
= d1 – σ * sqrt(t)
C = price of a call option
P = price of a put option
S = price of the underlying asset
X = Strike price of the option
r = rate of interest
t = time to expiration
σ = volatility of the underlying
N represents a standard normal distribution with mean = 0 and standard deviation = 1
ln represents the natural logarithm of a number. Natural logarithms are based on the constant e (2.71828182845904).
Rate of interest may be the relevant MIBOR rate or such other rate as may be specified.
The base price of the contracts on subsequent trading days, will be the daily close price of the options contracts. The closing price shall be calculated as follows:
If the contract is traded in the last half an hour, the closing price shall be the last half an hour weighted average price.
If the contract is not traded in the last half an hour, but traded during any time of the day, then the closing price will be the last traded price (LTP) of the contract.
If the contract is not traded for the day, the base price of the contract for the next trading day shall be the theoretical price of the options contract arrived at based on Black-Scholes model of calculation of options premiums.
\”
As I understand, once derivative of contract added with new expiration date, then only balck-scholes formula is working to decide the option base price after that only BID-ASK is working i.e. supply and demand only. I think price is decided on that not delta, gamma, vega or theta, or I\’m totally confused with option pricing.
Could you help me to understand?
Thanks,
Mayur
So the way to think about it is – how do traders bidding and asking arrive at their price? They must have a perception of what price to bid and ask for? This is where B&S option pricing comes into play.
Are you trying to tell me that only BID and ASK prices decide the price of derivative instead of underlying?
It is a combination of all things, Mayur.
Yes, Karthik I know that it is international market, but my question is why it\’s moving when underlying is not moving?
It is the perception that the underlying will move when the makrets open, that idea makes the futures move 🙂
Sir, suppose I buy options, for example, I held it for one week, if price went up during those one week and my analysis are correct, will theta decay still affect my profits.
To sum up, in buying options , do theta decay matters even if the price is going up, or theta decay affect on if price went down in option buying.
Yes, theta decay will happen, but the loss via theta decay will be set off by the gains in delta and volatility.
Karthik,
My question is not related to option but its related to derivatives i.e. future
Consider below:
1) Indian Market timings: 9:00 AM to 3:30 PM
2) GIFT NIFTY timings:6.30 am to 3.40 pm and 4.35 pm to 2.45 am
Now if GIFT NIFTY is future derivative of NIFTY, then why price of GIFT NIFTY is changing when market is closed? since GIFT NIFTY is changing while NIFTY is not changing.
Could you just explain what is happening??
Thanks and Regards,
Mayur
Because it is considered an international market, Mayur.
Sir, will theta decay affect my position if I hold it for 1 or 2 days. And for the 2nd question, if i buy PE then am i also on the option buying side or does it apply for only CE. Sorry for the question it may sound stupid , but I am new to options. Thank you.
Sam, so for 1 or 2 days theta decay may not matter much, but only if you\’ve bought early in the cycle. If you buy closer to expiry, then it will impact your position.
Option buying is same for CE and PE, does not really matter.
1) Think of it in terms of daily theta loss, easier that way.
That\’s means due to Theta premium is erodes at EOD only not during intraday.
Am I right?
Yes, that\’s right. Technically, it is continuously eroding, but it is easier to think of it and build strategies by assuming its a EOD thing.
Hi Karthik,
Could you please clarify two things on Theta:
1) Clearly Theta is depreciating the option premium but due to Theat, option premium lost its value by days or by hours or by minutes or by seconds?
2) if it is depreciating daily or hourly or minutely or secondly then it would be market days or all the days, market hours or all the hours, market minutes or all the minutes, market seconds or all the seconds?
Thanks,
Mayur
1) Think of it in terms of daily theta loss, easier that way.
2) Ref the earlier comment.
Sir I have already bought an option which is in decay, in this situation should I sell or what
I mean premium decay
What should I do in option decay situations?
Just need some recommendation
You can benefit from it by selling options, Saroj.
Karthik Sir,
I have a question, I was looking nifty option chain for october expiry. The ATM strike\’s(19400) theta is -2.5 . My question is that in every trading day -2.5 rs will be deducted from the premium amount and gradually the value of theta will also arise with time ?
On one hand, theta reduces the value and on the other hand, there are other factors that also reduce or increase the value of the premium. So look at it from a complete perspective.
Mere ko bhut ache se samjh me aya sb kuch bhut betreen tha bs Hindi ke kuch word complicated the
\”For example, if an option writer has sold options at Rs.54, with a theta of 0.75, all else equal, the same option is likely to trade at – =0.75 * (3**) = 2.25 = 54 – 2.25 = 51.75 Hence the seller can choose to close the option position on T+ 3 day by buying it back at Rs.51.75/- and profiting Rs.2.25 …and this is attributable to theta! Have a look at the graph below –\”
Sir, I could not get this – how you got the \”3\” number here, if the option seller sold the premium at 54 rs , then next day the premium will become (54-0.75) 53.25 rs. is it correct ?
You mean 3 in T+3? Thats indicates the number of days.
Dear Karthik sir, as you said above,
1. In case of Weekly expiry, if contract is created on Tuesday, I can expect theta peak on Friday? But the contract itself would have
already closed on previous day, Thursday itself.
2. In case of Monthly expiry, you say that the theta peaks around 4th day so it\’s 4th of the month. But the chapter says that it peaks
during the last week of the month.
Please clarify these anomalies.
1) The peak is on expiry day, post expiry, there is no contract, and there is no question of theta peaking.
2) In case of a monthly contract, the peak happens around the last week of contract expiry.
My question was quite simple sir. Just as in case of monthly expiry, theta decay is the max during last week,
so in case of weekly expiry from which day onward theta rises rapidly?
It peaks around the 4th day of contract creation.
Dear Karthik sir,
I know that sir. But what I wanted to know is that in a weekly expiry series, from which day onwards theta decay starts
effecting more.
Regardless of which expiry, theta decay starts at the time of contract creation.
Dear Karthik sir
In case of Weekly expiry series, from which day Theta starts playing out more?
Please help sir.
Theta is at work the moment the contract is created.
Hi Karthik, have you covered the behaviour of Theta for OTM, ITM & ATM options in a separate article?
If yes, please do point me in that direction.
Thanks again for all the great work!
Siddharth, yes I\’ve discussed this across greek interactions and in the query section.
Sir,
We learnt that option premium varies with underlying through the effect of Delta & Gamma. Now, while studying the chapter of Theta, we come to learn that Premium= Intrinsic value+Time value. Now, intrinsic value is purely based on underlying\’s price traversal.
(i) I want to understand if this intrinsic value effects through the involvement of Delta & Gamma or it affects separately.
Your reply on the above will help me get deeper.
I am waiting for your kind reply.
Yes, it does. No option greek works in isolation, eventually, they are all interconnected, and you will have to understand how it impacts the option premium.
Sir,
I studied upto Theta. With this, Please correct me if I am wrong in below statements:
Without consideration of volatility (vega), the premium of a strike (CE/PE) changes as per below:
(i) As long as a strike is in OTM domain, premium changes with changes with delta, gamma, theta abut not intrinsic value (since it is 0). Here changes of premium with change in underlying is only reflected through Delta & Gamma and not IV.
(ii) With the strike being flown to ITM domain, premium changes with changes with delta, gamma, theta and intrinsic value (since it is +ve). Here changes of premium with change in underlying is reflected through Delta, Gamma as well as IV.
1) Yes. Intrinsic value kicks in only after the stock becomes ITM
2) Thats right.
Great. Thank You.
Happy learning 🙂
Please note, above Buy call option. Strike 17350 CE
Dear Karthik Sir,
We observed the following details from payoff chart as below
Nifty 17359.75.
B/S Expiry Strike lots price
B 06 Apr 17350 1 100
When price is at 17380,
Expected P&L on
Mon, 03 April -775
Expiry day -3500
we understood here that total loss on expiry is (3500) . (PL=Spot-strike-premium paid=17380-17350-100=-70, total loss=-70*50=-3500 )
1. What about on Mon 03 Apr loss (775). This is because of time value is higher start of series? How can we calculate this loss?
2. Delta of the option=+.52 (from the option chain).
premium is supposed to increased by (17380-17359.25)*0.52=10.79 , from this premium increased can we correlate with PL.? if we sell on 3rd April.
Thank you very much for your great support.
The P&L can be different based on for how long you intend to hold the position. For example, on expiry, its purely based on the intrinsic value of the options, but if you hold the position during the expiry, many factors are at play (mainly the greeks). I guess Sensibull gives you the payoff before expiry.
Remember, Deltais just one factor to impact the premium. There are others as well like vol and theta.
Thanks a lot Karthik, but the premium decay i observed was not on expiry but what I observed was on the first day of the expiry series.
I read in the comments where you stated that for intraday trading Theta doesn\’t have much impact. If that is the case, time decay factor may not be the one that caused the decay isn\’t it. Not sure, but wanted to understand what could be the reason if it is not time decay.
Thank You
Got it, if its not expiry and other days, especially early in the series, then it can only be attributed to the drastic change in volatility. Remember, volatility also impacts the way option premiums are calculated.
Hello again Karthik,
Hope you are doing good.
Today for the first time I observed Nifty to see how it is moving and how premiums are moving correspondingly. (I actually observed the market yesterday to see how markets works on expiry day, but today I stuck my eyes to the screen and observed every single movement)
All Thanks to you for the way I progressed in my journey in Options learning.
Today momentum in Nifty was very very slow. I I was observing 17,200 CE April 6th Expiry when the spot was around 17,230 the premium was 130. Market kept on trading in this zone (17,200 to 17,250) for almost 45-60 min, what I observed is, initially the premium was increasing whenever the spot was increasing but after it traded in this zone for an hour so the premium didn\’t increase much even when the spot increased considerably. In fact the same strike was available 130 even when the spot moved to 17,250 (Remember I saw the 130 premium when spot was 17,230).
What is the reason for this? I tried searching google and watched some youtube videos but wasn\’t clear on their explanation. The common term they used was premium erosion or premium decay. They are sayin the Market is trading in the same zone for long time to erode premiums. I honestly didn\’t understand what they meant.
Can you please explain me what it means by premium erosion/decay and why it happened.
From this chapter I understood about Time Decay factor (but since I am looking at intradat perspective, time decay factor shouldn\’t be high right?)
Looking forward for your explanation as usual 😊
Thank You
Sai, so with passage of time, the option premium reduces. This, as you know is called time decay. The rate at which the time decay happens keeps increasing as the expiry progresses. The acceleration starts to peak on expiry day (maybe around post-noon), and even if the market increases, the time decay kind of weighs in and drags the premium down, unless the movement in the underlying is strong. So this is exactly what you noticed in the market.
Thank you very much.
Sure, happy learning 🙂
Here Time value calculated based on the price of the underlying
(spot) as below.
\”Spot Value = 8531
o Strike = 8600 CE
o Status = OTM
o Premium = 99.4
o Today’s date = 6th July 2015
o Expiry = 30th July 2015
Intrinsic value of a call option – Spot Price – Strike Price i.e 8531 – 8600 = 0 (since it’s
a negative value) We know – Premium = Time value + Intrinsic value 99.4 = Time
Value + 0 This implies Time value = 99.4! Do you see that? The market is willing to
pay a premium of Rs.99.4/- for an option that has zero intrinsic value but ample
time value! Recall time is money Here is snapshot of the same contract that I
took the next day i.e 7th July\”
When we checked the option chain , we observed that actual time value calculated based on futures price.Please if you explain why this difference, it will be very helpful for us.
Thanks.
Prasanta, so for option pricing, its ok to consider futures price but settlement is always with spot.
From the point of option seller, What will happen if i let option contract expires worthless? How much money i will earn or will i lose entire holding or will i lose just the profits? Kindly guide.
You will earn the entire premium, Aditya.
Thanks a lot Sir🙏☺️. Started with your fundamental and technical analysis chapters like one and a half years back. Pretty impressed with the explanations especially about income statement, balance sheet and cash flow statements. Use them almost daily when I read a financial statement. I found only one other book impressive apart from that on balance sheet thereafter. All your options materials are in a PDF format with me always in all my devices. Highlighted, Bookmarked them. Comes in handy all the time. And the cherry on top of it is that I\’m able to connect with the author. Watching all of your youtube videos as well. Nice presentation and good editing. Can\’t ask for more. Wish I was given this quality of financial education during college days. Happy to learn from one of the best. Please Keep educating us sir!
Thanks for letting me know, Sathish. This motivates us to do better 🙂
Happy learning!
Does theta decay happen during trading holidays, weekends also? Thanks Sir.
Sort of, yes 🙂
Thanks for the reply. But I didn\’t catch you Sir. Isn\’t the IV I gave(460) the associated IV? And LTP at that time was around 433 only. The reason I mentioned the narrow bid ask spread is because I thought it translates to high liquidity. Is there anything I\’m missing in terms of lack of liquidity? I still don\’t understand what I should be looking for?
Ah, I missed your point on the narrow bid ask. Yes, a narrow bid-ask represents higher liquidity. So assuming ample liquidity exists, the option should not trade below its intrinsic value; even if it does, algos will pick up such an anomaly and plug the gap.
18000 PE March. Yesterday it traded around 610. Even as of writing this the intrinsic value for 18000 PE itself is 460. (NIFTY is around 17540). Premium is around 433. Bid ask spread is very narrow like hardly 1 rupee differencel. I don\’t understand how it is trading below intrinsic value.
Check the liquidity once Sathish, and not just the last traded price. What you need to look for is the last traded price and the associated intrinsic value at that point. For example, the lack of liquidity may result in thin trading activity and while the spot has changed, the LTP reflects a price at old IV. So do check for LTP along with the associated IV at the time of trade.
Currently NIFTY is around 17340. But the premium for March monthly Put option is around Rs.610. Intrinsic value itself is 660. Added with time value it should come above 660 right? I don\’t understand how this option premium is trading below intrinsic value. Please clarify sir.
Which strike are you referring to? Yes, the option cant trade below its IV. Do check the bid-ask for a more accurate view on the price.
I have sold OTM Option and its going against my view point hence there is a increase in the premium however I am closer to expiry and market stays near to breakeven as the premium went high will i still get the benefit of entire premium because i contract closed just an inch below expiry even though high premium?
Yeah, as long as the spot is below the strike for call and above the strike for PUT, the option will expire worthless, and you will get to retain the premium.
How can we calculate theta value for each day until time of expiry?
YOu can look up on any Black & Scholes calculator for this.
Hi Karthik, thanks for your revert. Actually I want to understand at what theta value I should exit from the loss making leg to avoid further decay. The leg which will become ITM will be hold till expiry.
Regards
Rahul Chaudhary
Theta accelerates as you move closer to expiry. Again there are other factors at play here…delta, vega etc. So taking a call just based on Theta may not help.
Hi, good morning. I am an option seller but this time basis some past studies for budget month, I have bought BNF 40600 (Both PE and CE) 23rd Feb expiry.
Seek Your views that at what theta value I should exit the leg which is in loss rather than waiting till expiry or till what date I should hold the loss making leg.
I do take the same trade on weekly expiry.
STUDY – https://twitter.com/kirubaakaran/status/1619999152775249920?t=aCgCAGeBne4MB7ZBVfrS2A&s=08
Regards
Rahul Chaudhary
Can\’t really advise you on when to exit, but if you are a seller, then the theta decay accelerates close to expiry and your best bet is to exit then 🙂
\”All other things being equal\” there would be no market.
I mean, all other forces acting on option premiums. To make the concept easier to explain 🙂
Sir does Theta decays even on Saturdays and Sundays?
Sort of, it does.
Thank you for your answer sir.
By the way I have another query sir
For Nifty current month option ATM theta decay is less for the first half of the month when compared to second half. So is it good to use long strangle/straddle for the first half of the month and short strangle/straddle for the second half of the month? I know its all depends on me and other Greeks but I wish I get clear answer from you sir.
Thank you inadvance
You are right, the theta decays at a lower rate in the first half as opposed to the 2nd half. So if at you want to buy options, its best if done in the first half.
Hello Karthik sir,
theta decays affects the premium price on the end of the day or each and every minute/second of the day or movement of the premium price sir? (consider when other things being equal)
It is on a continuous basis, Sudharshan.
Thank you sir….
Hi sir,
Today though spot was above my strike price ,actually premiums were not moving when strike crossed the spot.
There are still three days to expiry.
Hw timedecay affects ATM calls.
It is not just about time decay. Other greeks too play a role in this.
I have seen theta decay which is higher than option price ! eg,
Theta decay = -8.459804206
Option Strike = 18000 CE
Underlying = 17786.80
Option Price = 43.4
IV = 12.63
Days to expiry = 6
total decay = -50.758 (theta * 6)
price = 43.4
Can you please explain this ?
But here you are assuming that the option price is just a function of time. But there are several other factors that act on option prices at the same time.
Theta decay = -8.459804206
Option Strike = 18000 CE
Underlying = 17786.80
Option Price = 43.4
IV = 12.63
Min_left = current_time(7.19PM) to 3rd Nov 3.30 PM
Decay per min = 0.00587 (Theta/24)
Total decay = 49.468 (Decay per min * minute_left) [Which is higher than option price]
How is this possible ? Could you please explain what I am missing?
I\’m unsure if you can divide theta and get a per-minute decay rate. Something I\’ll have to figure out. That said, a demand and supply situation also adds to the premium.
मान लिजिए कि किसी प्रीमियम का भाव 100 रुपये हैं। यदि उसमें (1 point ) की गिरावट हुई तो कितने प्रतिशत की कमी आयेगीं।
Hi. I understood the concepts so far. One question is that how do I choose which stock ( company) option should I choose?
So this decision of yours should come from your analysis on the underlying.
Why do some stocks have high decay and some stocks have lower decay?
Thanks in advance 🙏🏻
Depends on the time to expiry. The longer the time to expiry, the lower is the time decay.
Hello Karthik,
I may have a very basic question, but still here it is:
– If for an option contract, suppose the closing price (premium) is 50 & the Theta is 3. So does it mean by next days opening I will see the premium as 47?
– The Theta gets applied only after closure of one trading day? Or this Theta value is seen getting reduced from the premium within the same day itself?
Will the options also loose time value from morning to evening in a day, other than day to day decay.
It is a continuous process.
Hi Karthik,
First of all, thank you and your team for this wonderful content.
I have a query w.r.t to below statement made in this chapter.
\”For example, if an option writer has sold options at Rs.54, with a theta of 0.75, all else equal, the same option is likely to trade at – =0.75 * 3 = 2.25 = 54 – 2.25 = 51.75 Hence the seller can choose to close the option position on T+ 3 day by buying it back at Rs.51.75/- and profiting Rs.2.25 …and this is attributable to theta\”
Q1: T+3–> here does T refer to date & time of selling the option?
Q2: What does it mean \”Seller can choose to close the option position on T+3 day by buying is back at Rs.51.75/-\”? Could you please elaborate a bit on this, step by step.
1) T+3 means, trade day plus 3 days. So if you shorted on Monday (T), Thursday is T+3.
2) It means that you can close the position on that day.
You can sell options closer to the expiry – you will get a lower premium but the drop in premium is high- Why sir?
Because of the theta decay, Nikhil.
How can we calculate every hours theta decay ??
Not possible, you just have EOD calculation.
Sir please suggest me where do I learn option trading
You are in the right place 🙂
hi kartik
where can i find theta value of particular stocks???
You can use any B&S options calculator to get the Theta value.
Hello Karthik Sir, I completely understood how theta really works but couple of questions. Where can I find the real-time theta values that would tell me the impact of holding a specific contract for a given period of time? If I am of a view that Nifty in the current weekly contract would not cross 16100 then according to your statement that we should sell OTM contracts, in this case should I be selling 15900, 16000 or 16100 if the current spot price is 15850 & what would I be selling a CE or PE?
The decision to sell CE or PE, depends on not just your view of the market, but also your sense of which premium is expensive. Usually, with an increase in volatility, the premiums too increase.
Sir can you please guide how time is calculated for weekly options. For eg how time value is calculated for Banknifty on last day? is it calculated hour wise? if any guideline please share
Nirav, not sure if I understood your query correctly. Sensitivity of time is captured by Theta and it accelerates to maximum by end of the expiry, especially on the last day.
Time decay affect which strike price the most??
I mean in which strike price premium decreases very 1st ?? It is ITM OR OTM?
I\’d say ATM and OTM.
Dear Karthik sir,
The chapter says –
1. At the start of the expiry series, the seller has the advantage of pocketing a large premium
but the fall of premium happens at a low rate.
2. When closer to expiry, the seller gets a lower premium but the drop in premium is high.
Which of the 2 you suggest is better from your experience ?
Both, depending on your experience in the market 🙂
Dear Karthik sir,
From what I understood Theta decay for OTM > ATM > ITM. But what is the reason behind this behavior ?
Please explain.
Thanks
Thats just the way options behave.
Sir, Should one consider greeks at the time of option selling only ?
Both at the time of selling and buying.
Dear Karthik sir, Pls answer the below questions or if necessary try to add any important point also at each answer so that I remember next time. Below is the assumption data. Thank you
1) Should one taken into consider Option Buying only for intraday to get rid of theta effect for weekly+ monthly expiry for both stock + index option ?
2) For Option Buying, Should one consider only technical chart ?
3) For long stock + Index option, Slightly OTM strike price is good to select ? so that it converts to ATM and then ITM if my view is right
4) Spot: 8000, Strike Price:- 8200 CE, Position:- Sell. So this is OTM sell na ?
5) Spot: 8000, View:- Bearish, Strike:- 8200 CE (Sell), Delta:- 0.3, Premium:- 200. If spot increases to 8200 then my premium becomes 260 right ? If spot decreases to 7900 then premium becomes 170 right ?
6) Sir, If I buy/sell any option on Monday and then on Tuesday, If both this (Delta + theta) affect on my premium ?
1) If you are buying, then this is true especially if you are closer to the expiry. Not necessarily true if you are early in the series (more time to expiry)
2) YOu can combine both tech and fundamentals
3) Yes, that\’s a good outcome to aspire for
4) Sorry, don\’t get that query. Yes, it is a sell or a buy based on what you want to do
5) Theoretically based only on DELTA yes, but there are several other factors at play
6) Yes, not just delta and theta, gamma and vega and supply and demand, they all affect your premium.
So we can think of ATM as safe thing wrt Theta acceleration?
In terms of theta decay, yes, its slightly slower compared to OTMs.
I believe there would be slight change in the behavior of theta wrt ITM, OTM and ATM.
Please guide on that. Thanks
The theta acceleration would vary basis the moneyness of the option. Its higher for OTM and relatively lesser for ITMs.
Dear Karthik sir,
Pls explain theta vs time for expiration w.r.t ITM,OTM & ATM options.
You told you will be adding it in the module long back in 2015. It\’s 2022 and still missing.
Any info when we can expect it?
The most generic thing to note is the theta decay, which I\’ve already explained. Is there anything else you\’d like to note?
We have to use ATM strike IV but as market moves, ATM strikes also changes. So do we have to check new ATM IV or old ATM strike\’s IV?
Yup, keep track of ATM IVs.
I just checked theta values for 2 expiries- 24th March (Today expiry) and 28th April (around 1 month to expiry) for Nifty 18700 CE
Theta for 24 March expiry Nifty 18700 CE= -3
Theta for 28 April expiry Nifty 18700 CE= -0.25
as we are near to expiry, theta is more and when there is more time left to expiry, theta will be low. Then how can this happen? Near expiry (24 March) has less theta than far expiry(28 April). Please clarify
-3 is greater theta than -0.25 right?
Sir as you mentioned option seller has time risk of option expiring ITM so they ask for high premium as days for expiry are more similarly option buyer also has time risk of option expiring OTM then why we consider seller risk(high premium for there risk) and not buyer risk?
Sometimes when the premium shoots up due to increased volatility, then it makes sense to sell options rather than buy options, Abhishek. So it really depends on the market conditions and the wat options are moving.
Hi karthik,
On the expiry day, for intraday if my view is correct I can buy and exit the call option within couple of hours(before market closing), in this case the theta decay will affect the premium ?
Theta wont impact the premium much on a intraday basis, unless you are very close to expiry.
Please Explain the concept of VIX and how its value is defined…
Also please explain how the premium value is made..?
Do check the subsequent chapters, Dhruv.
SInce option value is the sum of time value and Intrinsic value i.e
Premium = Intrinsic Value + Time Value(and other factors)
and if the underlying value changes by 1 point then that implies that the value of intrinsic value should also change by one for ITM, which further implies that the for ITM Premium could change its value by Equal to or more than one point w.r.t change in underlying value by 1 point. But Delta could not be more than one. Can you tell where I am wrong ?
Harman, if it\’s ITM (deep ITM), then one point change in underlying leads to 1 point change in the premium. In fact, for this reason, deep ITM option behaves like a futures instrument.
sir in the last graph shouldn\’t it be Time value vs Time to expiry??
Since we comparing to time to expiry, it represents the movement of time 🙂
How the theta is calculated in Nifty or Bank Nifty options with weekly expiry with a Holiday in between? For e.g. last week of January will have only 4 days with 26th January as a holiday. 27th Jan is the expiry day (Thursday). Will the theta benefit on Wednesday be given to the options on Thursday morning ? Or is it distributed proportionately among actual working days in a week? How is the theta calculated if there is a holiday in between?
It will be considered equally across all days remaining for expiry.
Hi Karthik, I have a query regarding the theta decay graph. Will this be with respect to only OTM options? In an ITM option won\’t the probability of the underlying price closing below the strike price become lesser as time goes forward, thereby increasing the premium/theta value? Or does the concept of theta not come into play at all in ITM options?
Akash, theta decay is a generic principle. It impacts all options regardless of its moneyness. Of course, it is more for OTM as we approach the expiry.
So when everything else remains the same, time decay works in favour of ITM options, right?
Yes, in a sense the decay is slower for ITM options compared to the OTM options.
Hi Karthik,
Suppose I buy a far ITM CE 2 days before expiry, shouldn\’t the premium increase the next day due to time decay? (considering everything else remains the same).
Rationale behind this – As expiry day approaches, the probability of CE ITM option to remain ITM increases.
That probability is already baked into the premium, Amit.
How does theta decay works over weekend in weekly and monthly options. Will option loose theta value considering 5 market day or 7 calendar days in weekly options ?
Considers all days of the week, Pawan.
Hi Karthik,
It is about theta and Decay effect.
Actually, I want to know when theta and decay effect on the premium price kicks in.
First is, what is decay effect? is it same theta or something different?
Second is, for example, when the theta & decay effects come on premium price if I buy a particular strike around market closing time (i.e., 3.15 pm)?
Is it happening after market closing hours (i.e., between today 3.30 pm to next day 9.15 am)? Or
Same day at 3.30 pm? or
Has the price at 3.15pm itself included theta effect for next day? or
Next day morning at/ or after 9.15 am? Or
Next day from 9.15 am to until market closes, this effect will happen continuously? Or something else?
Thanks,
Lingam
Decay effect, time decay, theta decay all refer to the same thing. The phenomenon where the time value of the option is lost due to the passage of time is called theta decay.Theta decay happens on a daily basis, it is accelerated closer to the expiry. Don\’t bother much about exact timings and all.
Time decay graph
1st point
At the start of the series – when there are many days for expiry, the option does not lose much value. For example, when there were 120 days to expiry the option was trading at 350, however, when there were 100 days to expiry, the option was trading at 300. Hence the effect of theta is low
Sir what is tha theta value at 350..how to find
Rakesh, I\’ve explained theta in great detail in this chapter itself, Rakesh. Suggest you read through this again.
Hi Karthik, I\’m learning a lot from your articles. Do options premium changes based on buy/sell volume excluding greeks, iv, underlying movement?
Yes, the demand and supply situation in the market does have an impact on the premium, but not to the extent of the option greeks.
Hi,
Does THETA affect intraday trades ?
Is it negligible for intraday ?
IF NOT THEN
How should it be used to measure risk for intraday ?
?????????????????????? ??????
Graph regarding the change of Theta in all cases: ITM, OTM, ATM
Sir, i have one doubt that if market is sideways and on Trading tick website i have observed Premium is Decay is
CE premium change is 1159
PE premium change is -2059
my doubt how to calculate decay percentage and which side has more decay.
Thanks
You can look at the option greeks for this, look for Theta in particular. Higher the theta value, higher is the decay.
Sir, can you pls update how theta will behave with OTM, ITM and ATM options as asked above by Amit Pathak.
Thank You
Sure, but in a nutshell, the rate of decay is highest for ATM and OTM, lower for ITM.
Every time I read any chapter of varsity i find something new to learn
Very precisely written
Very helpful sometimes confusing also …
Happy learning, Soundnya 🙂
Hi,
I need to clarify for the entry in call options… May this question already asked by anyone one on their view. Asking from my side for understanding…
Say for example, Nifty trading on 16250 ryt now,
If I bought in 16200 CE (ITM), the market down below 16250.. still am I in profit side??
may I buy 16250 ATM is safe or 16200 ITM is safe?? Not considered the premium.
Pls clarify it.
There is nothing like a safe strike to trade, its the strike which has better odds of closing ITM upon expiry. But generally yes, staying in and around ATM is better than going OTM.
Dear Karthik,
amit pathak says:
July 9, 2015 at 9:28 am
Sir,
Pls explain theta vs time for expiration w.r.t ITM,OTM & ATM options
Reply
Karthik Rangappa says:
July 10, 2015 at 5:11 am
Amit, makes sense, not sure how I missed this…I’ll probably make an addendum to this chapter.
Reply
The above topic on theta vs time for expiration w.r.t ITM,OTM & ATM options is still awaited. It\’s be 6 long years. Looks like theta (the graph guy) for this one is asleep somewhere.
Thanks for the reminder. I\’ll try and get this done sometime soon.
Hi rangappa ji, you said you will add addendum about how theta changes with time of OTM, ITM, ATM options in one of the comments initially, is that added somewhere? I am not able to find it.. Thank you
I need to check this 🙂
Sir, in a monthly premium after one week, which will decay more…. deep OTM or near OTM assuming that market is range bound , plz clarify..
Deep OTM.
Is time value decay truly on daily basis ? I see on the expiry date option value decreases within few minutes. If option time value decays truly on daily basis then if i buy option solely for intraday basis than theta decay does not effect me, am i correct ?
Dear SIr,
Can you explain the weekend effect and the change in IV during the second and last week of expiry and its effect on theta?
Weekend effect is the perception of option premium losing its value owing to the passage of time on Saturday and Sunday.
Hi
I have observed that for OTM options the theta is greater than option premium on Wednesday. For example on Wednesday after market closure the premium of 15000 PE was 5 where as theta of 15000 PE was 8. How is that even possible that the decay is greater than the premium itself?
That\’s possible, think about it…what real value does an OTM option have? Nothing right? So whatever value is attributed, its for the time.
So, what if i sell a call OTM well ahead at the beginning of weekly expiry? will i risk a huge amount, or will get profits?
No, but do track the position closely. You don\’t want to be in a position where the OTM position transitions into an ATM or ITM position.
There must be a mathematical expression to reach the premium value. It is more important to understand that to take a decision what is the best time to take a call or put option. Shall be thankful if anyone can share the mathematical equation.
Yes, that\’s right. You can use the B&S option pricing formula for this.
Option buyer makes loss if premium goes below his premium paid price
Option seller makes money either way the option premium moves
I m assuming I won\’t wait till expiry
Yup, thats correct.
Say I\’m option buyer
I pay a premium of 60 and
If premium goes high I make money if premium goes down I lose money
Even the premium rises to 75 I don\’t need to wait till expiry and get out next day
I can sell the contract at 75
Yes, you can sell at 75, no need to wait till expiry.
Sir how fall in premium favours option seller
Say I write an option and collects premium 60
If nothing else changes due to time decay the option value comes to 55
How is option seller made profit
You sold at 60
You bought it back at 55.
You make a profit of 5.
If you look at the same transaction in reverse order –
You bought @ 55
You sold @ 60
Hence made a profit of 5.
Both are the same, the order of trades is different.
Hi Karthik, can you explain theta vs time for expiration w.r.t ITM,OTM & ATM options
The effect of theta is highest for OTM, followed by ATM, and ITM.
Why not premium of call and put option is same for the same underlying, strike price and time to expiry ?
These have their own demand-supply dynamics, Ashwani. That impacts the prices.
Thanks Karthik
Good luck, Ram.
Hi Sir,
kindly please clarify on the most optimal selection of strike price for the following scenarios
1)Lets say nifty is trading 14850 as per spot chart . on the weekly expiry day I expect the market to move up and I prefer selling OTM put option as I am bullish towards market
In this case which strike price to select provided if my direction is correct
2)lets say nifty is trading 14850 as per spot chart and I expect the market to move down and I prefer selling OTM call option as I am bearish towards market.
In this case which strike price to select provided if my direction is correct.
As option sellers have edge i.e if market is in sideways or bullsih (if my direction is bullish view) and if market is in sideways or bearish (if my direction is bearish view) .I will keep stop loss based on the spot chart and based on my directional strategies as for option seller risk is unlimited and profit is limited.
Kindly please clarify .
On non expiry days ,I am going to follow the below plan .please correct me if I am wrong.
1)for weekly expiry ,on friday which is starting of the week ,I am bullish and nifty is trading at 14850 on spot chart ,and I will select 14850 ATM option and buy 14850 ATM call option with stop loss
2)for the same ,if I am bearish ,I will sell ATM call option stop loss ,provided if my direction is correct.
Thanks in advance
kind regards,
Ram
1) You can use the standard deviation concept to identify the range, have explained that later in the module
2) Same as above
Yes, this is ok. I\’d suggest you paper trade for few weeks before you deploy the trade.
At which strike I mean ITM, ATM, OTM has more Theta decay
OTM, ATM have higher Theta.
is it theta will affect premium on intraday basic, if yes then where can I check that
Not on an intraday basis, but it does on an EOD basis.
Dear Sir,
Unlike the other options, theta does not change its value during the day right?
Obviously the theta value increases daily but unless you count it theoretically it should stay roughly the same during the day?
Thats right. But Theta value only decreases with time, won\’t increase.
Sir,
Pls explain theta vs time for expiration w.r.t ITM,OTM & ATM optiodont
think you have not answered this
Theta decay is highest for OTM and ATM, lowest for OTM. This accelerates as you move closer to expiry.
Thank You ; Sir.
Good luck, Lionel 🙂
SIR;
AS WE KNOW THAT THE THETA INCREASES EXPONENTIALLY AS WE APPROACH CLOSER TO THE EXPIRY ; AND HENCE DECREASING THE TIME VALUE DRASTICALLY ( ESPECIALLY FOR ATM OPTIONS ); BUT I WANT TO ASK YOU; ABOUT THE BEHAVIOR OF THETA AND TIME VALUE FOR THE WEEKLY OPTIONS IN ( INDICES ); DOES THETA ALSO INCREASE EXPONENTIALLY AS WE APPROACH THE WEEKLY EXPIRY FOR WEEKLY OPTIONS ?
Not exponential, but yes, theta decay is on the higher side as we approach expiry.
THANK YOU .
Good luck!
THANK YOU SIR FOR SOLVING ALL MY QUERIES IN A SIMPLE AND UNDERSTANDABLE WAY.
AND PLEASE HELP ME WITH ONE MORE QUERY THAT I HAVE .
1. DO TIME DECAY TAKE PLACE ON HOLIDAYS AND WEEKENDS ALSO ?
Yes, Lionel. It does.
SIR;
FOR EXAMPLE SAKE IF THE TIME VALUE FOR \”ABC\” STOCK OPTION ; TODAY IS = 10 AND THE THETA CURRENTLY IS \”2\” ; HERE ARE MY QUESTIONS
1. FOR TODAY INTRADAY TRADE WILL THE TIME VALUE CHANGE ?
2. AND IF THE TIME VALUE CHANGES ON INTRADAY BASIS ALSO THEN WHAT IS THE FACTOR TO CALCULATE THIS CHANGE AS ; THETA IS CHANGE IN TIME VALUE PER DAY PAST ?
3. AND WHILE CALCULATING DAYS LEFT FOR EXPIRY WHETHER WE HAVE TO CONSIDER ONLY THE TRADING DAYS OR WE HAVE TO CONSIDER ALL THE DAYS ?
4. AND IF WE HAVE TO CONSIDER ALL THE DAYS THEN WHILE CALCULATING THE ANNUALIZED RETURN OR VOLATILITY BY USING DAILY RETURN AND VOLATILITY ; WHAT SHOULD BE THE MULTIPLICATION FACTOR WE SHOULD USE ( 252 ) OR ( 365 ) ?
1) Not really, but may change rapidly on expiry days
2) As I mentioned, does not really matter
3) Trading days
4) 252
Sir;
AS WE KNOW THAT THE TIME VALUE OF PREMIUM DECREASES AS THE TIME TO EXPIRY APPROACHES CLOSER; BUT WE USE THETA TO CALCULATE THE DECREMENT IN TIME VALUE AND THETA IS DEFINED AS \”POINTS LOST PER DAY ON PREMIUM\”; DOES THAT MEAN THETA DOES NOT DECREASE THE TIME VALUE CONTINUOUSLY ( ESPECIALLY ON A INTRA-DAY BASIS ) RATHER IT DECREASES THE TIME VALUE ONLY WHEN THE DAY IS PAST AND DO NOT DECREASE THE TIME VALUE SECOND TO SECOND ?
SIR; PLEASE REPLAY BECAUSE I WANT TO USE A OPTION STRATEGY BASED ON THIS CONCEPT.
Thats right, you will not experience theta decay on an intraday basis (unless you are close to expiry). Theta decay in quite tangible on a day to day basis.
Thanks got my doubts clarified in full
Good luck!
Hi Karthik,
Thanks a lot for clarifying the doubt.
One more doubt.
1. In the above scenario, if the spot price reaches 2700, then my put option will be ITM and hence I would gain. However, my call option would be worthless. Please suggest on this point if I am correct.
2. Further, Seeking a little more insights as per your point 3. If there is no momentum and the spot price moves sideways, I am bound to loose entire money at expiry due to time decay. So, How will a low momentum be helpful?? I was of a impression that if the momentum is high in one direction, I would make good profit from at least one of the trades?? Please suggets if I have missed accounting for any critical variable.
—
Regards
1) Yes, provided you are long 2700 PE.
2) In case of low momentum and the sideways market conditions prevail, you can consider options selling and benefit from theta decay.
Hi All,
I have been in Equity and Futures trading for quite sometime i.e. 3 years.
I have a question related to Options trading as I am new to it and look forward to your support.
Paramerters:
Stock Name: TCS
CMP: 2902
Date: 26/12/2020
I Plan to buy one lot of TCS JAN 3000CE @ Premium of 67 and simultaneously buy 1 lot of TCS JAN 2850PE @ Premium of 69 expecting TCS to fall to 2750-2700 levels but minimising my loss in naked put option by buying a call option as well also expecting volatility to increase by 15th Jan 2021
Doubts:
1. Will this be a long straddle strategy?
2. What are the odds of me loosing the entire money.
3. Is it advisable to play with this startegy or long stradlle is applicable and suggested only at ATM with expectation of High Volatility.
Regards
1) This is a long strangle, not straddle.
2) If markets gain momentum and move in either direction, then you will lose money
3) Both these strategies are similar in their behaviour. Depends on how the market momentum. Higher the momentum, higher is the probability of you losing money. These strategies are best executed when you don\’t expect much movement in the market.
Dear Sir,
Can you please add an explanation for ITM/ATM/OTM options (theta vs time to expiry)?
Please do check this chapter – https://zerodha.com/varsity/chapter/moneyness-of-an-option-contract/
sir why theta increae and decrese in intraday. please reply
Theta does not increase, it only decreases as we move closer to expiry.
Does theta decay happens throughout the day? Meaning if the delta is zero will I see an increment in p/l with every tick or will it get added to the account after day closing? ( from option seller perspective)
It does, but it is more recognisable on an EOD basis.
By saying that option buyer loses money on day to day basis you mean that the earliest he gets into contract i.e. from maximum number of days to expiry, the better for him.
Hmm, that is possibly good for the sellers.
hi sir…what does total theta 1200 means??
1200? Where are you getting these values from, Neev?
Hi Karthik..good day to you. Your team\’s and especially your replies have definitely added a special set of skills in my life.
My query today is on the theta of deep OTM strikes. For example, weekly nifty expiry, strike of 11700 has premium price of 7.5 rs and theta today(tuesday) is 6.79
How does this work? 6.79 a day doesn\’t add up at all, and I cant say 6.79 is for tomorrow either, because there are still 2 days to expiry.
Why I\’m asking this, I want to get out of a position where I have already realised around 80-85% target profit, and get into another position. For that, I want to calculate ahead when I can realise that 80% mark.
In this example, from the looks of it, 6.79 should decay tomorrow itself, but I don\’t think that happens practically. There would still remain 2 or 3 rs tomorrow, right?
Is the gap entirely attributale to demand/supply price? If so, can you steer me to a direction where I can calculate that 80-85% range and when exactly I might realise that (except of course on expiry date opening, where a deep OTM definitely loses almost 95% its value)
Thanks
I quite doubt the theta value is correct. However, this is a weekly option and the theta decay is quite rapid. Also remember, while on one side the theta decreases and on the other there are other factors which influence the premium.
Hi Kartik,
Reduce of premium due to time should constant even if all other factors are variable. Because time factor is fixed For e.g.
Option – Nifty
Premium – 100
Expiry – Weekly
Premium reduction due to time should be –
100/7= 14.28 per day.
Time Reduction should be constant. However premium can fluctuate with other factors too.
Also I want to know when preimum loss its value due to time at the beginning of next day when market starts 9:15, or it keeps loosing during day. Or in a trading day what are the time when system reduce its premium value due to time effect. Please reply. Thank you
No, its not constant, reduced gradually and picks up momentum closer to expiry. Again, the decay is uniform through the day.
sir,
It is still not clear that will time decay our premium per second hour or day because acc to definition of theta it will affect overnight but as per my experience keeping all other aspects in mind it is affecting per minute or hour?Is it true, if yes then how?
In reality, the theta effect is on a continuous basis, however, the change is not tangible especially early in the series. You can feel the change on the last 2 days of the expiry.
Thank you Karthik
Happy reading!
Karthik,
Thanks for the explanation, I got little bit confused. Since in earlier modules we learnt that , we can buy CE option by paying premium at lower price and sell when it increases before expiry and we can gain profits due to change in premium. But here it is said that, premium decreases as it is nearby expiry. So how both can happen in same time!! Sorry if am asking silly question.
Raj, you need to think about the option premium as a variable which gets influenced by various factors, which work simultaneously. The factors are called, the Greeks. While some tend to increase the premium, some tend to decrease the value of the premium. Theta is a greek which tends to decrease the premium as time passes.
Does the Theta decay happens overnight or over the weekend? It\’s a very common question but confused with the answers available over the internet.
Overnight, enhanced when we move closer to expiry.
hello sir
above ststed example of idea where there is 1 day to expire , there is time value of .3
you saif if there were 20 or more days to expire time value must of 5 or 8
how to calculate such thing ?
A standard Black and Scholes calculator will help you get the theta value Rajat.
Sir on the day of expiry can the trade be cash settled in place of physical settlement. Or is it important to take delivery of trades ; if it is then what will a person do who wants to exercise his rights but does not have sufficient amount to take delivery.
All stock F&O is settled physically, no option for cash settlement 🙂
Hi Karthik,
I couldn\’t understand the change in Theta value. I mean how is that calculated if that is not constant? For delta it was very much clear when price moves, there is second order derivative called gamma which controls the movement of delta. For Theta then with movement of time who controls its movement? Is there any formula how theta will change?
Yes, the formula is baked in the B&S calculator. In fact, every greek has a 2nd order greek including Theta.
Sir,
Pls explain theta vs time for expiration w.r.t ITM,OTM & ATM options
Request you to look through the chapter, I\’ve explained the same here.
Hello sir ,
Really good content
I have one question regarding option selling . you said that if we sell option at start of series , we have advantage of pocketing large premium . on the other hand, selling option closer to expiry , we will get lower premium but drop in premium is high .
but which one is more risky ?
This depends on other factors as well. But if you were to look at just this one angle, then writing early in the series is risky.
So what will be its significance? Analogous to Gamma?
Any recommendation for what to read?
Yeah, I don\’t think it has any practical use.
Is there a second order derivative of Theta? Or will that always be 0 as the Theta is constant?
But like you said when we approach expiry, rate of change of theta increases. So if its derivative exists then what will be its significance?
Can we draw parallels with Gamma and use it for estimation of risk?
Thank You in advance. 🙂
Theta is not constant, increases as the time to expiry shrinks. I\’m not sure about the 2nd order for Theta, I need to look up. But yes, intuition says it exists 🙂
The below section is confusing –
\”So if you are selling options at the start of the series – you have the advantage of pocketing a large premium value (as the time value is very high) but do remember the fall in premium happens at a low rate. You can sell options closer to the expiry – you will get a lower premium but the drop in premium is high, which is advantageous to the options seller.\”
Comment – As per my understanding if we sell option at the start of the series it is more beneficial as it will give more premium, while if we sell option closer to expiry it is not beneficial as it will give low premium.
While as mentioned in the section the later is more beneficial as you have stated – \”you will get a lower premium but the drop in premium is high, which is advantageous to the options seller.\” Can you please clarify.
This means to say that its ok to get lesser premium (when you write) as long the rate at which it will drop increases rapidly, which is what happens when you sell options closer to expiry.
Hi Sir, Can you please explain theta vs time for expiration w.r.t ITM,OTM & ATM options.
All else equal, options tend to lose value as the time to expiry approaches. OTMs and ATMs have a higher Theta value compared to the ITM.
Hi Karthik,
my question is not related to this chapter. I want to know if there is any place that could provide me with option premium data which roughly shows future value according to inputs given by me. Like underlying price, days to expiry, volatility.
eg: if i sold 25JUN2020 , 10000 CE@ 80 rs. and spot is at 9500. I want to know in advance at a given price point what will be the value of the premium i sold. There are many places that shows profit and loss in graphs wrt to price and expiry. Iwant to know option premiums.
If there is no such place, can you teach or give some suggestions on how i can calculate on my own.
I want to know this to test and learn option adjustments. To have some idea on how to adjust trades when i enter sudden losses.
PS: I tried explain clearly but i dont know whether it is clear enough. Thanks in advance 🙂
Yes Lokesh, you can use the strategy builder from Sensibull and see the projected payoff – https://sensibull.com/
Hi Karthik,
Thanks for the answers, i was looking for more depth to my questions, so i have googled and understood.
I\’m enjoying the modules. You have really done a wonderful job of simplifying and explaining to depth. Kudos to you. Also i appreciate your idea of feeding the people with subject rather one time food (calls).
Once again thanks for the simplified modules. Will get back to you if i have doubts moving further.
Regards,
Karthik
Happy reading and trading 🙂
Hi Karthik,
Thanks for the nice content. I have few doubts,
1. What could be range of Theta? If different for each stock then please give example for nifty.
2. Is theta value same for all stocks with equal no of days to expire, say 30 days to expire?
3. I have understood the effect of theta on OTM, but what about its effect on ATM & ITM?
3. Is theta highest at ATM? Is there any max. value? (again u can consider nifty as example)
4.
1) Yes, depends on the underlying
2) No, depends on the underlying price
3) The theta decay is slower
4) Yup, max for ATM. Check the graph.
Hi Kartik
I understood from a query asked earlier that Theta works on weekends and holidays too. But on fridays, shouldn\’t the call buyers discount for that fact too?
I have a case study here:
NIFTY underlying moves by 400. Delta is somewhere around 0.35 to 0.40 , Vega 8, Theta 32, Premium moves by only 55.
Could you please help me understand the math behind it, to a certain extent?
Are the buyers discounting for a 3 day weekend?
Thanks
Delta = 0.4, So for every 1 point, change in premium is 0.4, so for 400 points, it is 160 (400*0.4) points. Delta now changes from 0.4 to the extent of Vega. Premium declines by 32 points. Have explained this in the relevant chapters itself.
Dear Sir/Madam
I want make trading in F&O I’m new trader. Let me know How to do this?
1.As per my knowledge JUSTDIAL MAY 400 CE Premium price is 8.60 is there now (7-5-2020) I though stock will reach 400 within Expire day (28 May) & lot size is 1400. If i brought CE is for 8.60, if stock reach 400 within expire what would be my profit & when it fails to reach 400 within expire, how much loss i have to take risk. (1400*8.60=12040 Premium) Just dial equity price is now 335
If equity price will move from 335.340, premium price will raise?
In case again just dial falls from 335 & again reach this level after few days, same premium price will be there?
Thanking you
If by expiry, the stock moves higher than 400+8.6 = 408.6, then every Rupee above this point is your profit. In case it does not reach 400, then you will lose your entire premium. I\’d suggest you read the call option basics here – https://zerodha.com/varsity/chapter/buying-a-call-option/
Hi Karthik,
First of all thanks a lot for curating such a nice content.
I have 2 queries-
Sometimes I hold ITM strike overnight and find the LTP to increase slightly the next day morning before market starts.
Also during the day- suppose at Nifty spot 9230, the premium of a call option is 25. Now suppose spot dips to 9210 and after 20 mins again climbs back to 9230. In such scenarios, most often than not- price of premium is less than what it was initially (25 in this case)
Can both these be attributed to Theta ?
Not just theta Anusheel, depends on delta and vega also. Remember, the option premium is a function of all greeks acting simultaneously.
Hi Kartik,
In the comments section that was a request for theta vs time for expiration w.r.t ITM,OTM & ATM options.
Is there any update on this yet?
No, but the Theta decay graph should suffice, right?
Thanks Karthik, this makes sense.
Happy learning!
Hi Karthik,
Your way of teaching is impeccable. I\’ve been hooked since chapter 1. I although have a doubt, when you say –
\”He also knows that by virtue of time, there is a chance for the option he is selling to transition into ITM option, which means he will not get to retain his reward (premium received)\” – in regards to the option seller, if the underlying transitions into ITM , it means that the buyer has actually lost money since now the spot price is lower than the strike price he selected and hence the seller would get to keep his premium. Am I missing something here? Super confused.
Elvis, as an option seller I want the premium to go down from the point I\’ve written it. For example, if I\’ve written the option at 50, I want it to go to 45, or 30 or perhaps lower. The lower it goes, the more profitable I\’m. This also means that I want my option to expire worthlessly. ITM option on the other hands makes the option more valuable which implies that the premium is increasing, hence not good for me as a seller.
It is ok with your reply, there was no typo. I was telling about the example which I mentioned in the 1st comment.
Ya I understood this concept clearly. But why is it reverse in the above example. Please read my content one more time. For option buyer theta will be negative. But here why is it positive? that is what I am asking
Must be a typo, let me recheck.
Ya, but here my question is for nearby ITM option writers how come the theta is negative? It should be positive right? In a book it was given If you short an ITM call, theta will be negative and buying an ITM call will have theta positive, how come?
example given there:
ABC company – spot at 160
Strategy – Bearish ITM call spread
1. Long – 150 call
2. Short – 160 call
It is given negative theta and positive vega for the spread
After reading options material here, I directly opened that book to observe the examples, my guess for the OTM bull call spread is fine. But here my doubt is
ATM strike will have high theta and vega values compared to ITM and OTM.
here he shorted 160 call ATM which will have Positive theta and Negative Vega which will be higher than ITM call values.
Long call will have Negative Theta and Positive Vega
So net theta should be positive and Vega negative, right?
Here in the book it is give negative theta and positive vega for the spread.
Did I miss something in this entire topic? Correct me
I read all your chapters and modules related to options trading and strategies. That was really fantastic. I was like almost spent more than 6 months to learn the basics itself. But all under one roof. After completing the total covered concepts here, I felt very confident to invest my valuable time in learning this deep. I need your support to go further.
Thanks for your guidance till now. Let me know if the subject is not clear.
Chandra, its like this – it does not matter which option, call or put. If you are an option buyer, then time works against you. All else equal you as an option buyer will lose money in terms of premium erosion with the passage of time. Hence, to represent this fact, theta is -ve for option buyers.
Likewise, for option sellers, the passage of time is beneficial, as the option writers want the premium to reduce. Hence to represent this fact, the theta for option writer is +ve.
Hi Mr. Karthik,
Why is theta positive for ITM bullish and negative for ITM bearish? Usually for any long call theta should be negative and for short it should ne positive right.
Passage of time is positive for option writers and -ve for buyers, hence the convention.
Hi Mr. Karthik,
Ya, but this my doubt. Is there any technical reason that why 9300 and 9500 greeks were high by EOD yesterday. My question here is 9250 will have higher chance of ending in ITM than 9300. But how come delta of 9300 strike is high, same way vega as well.? and again 9400 strike delta and vega are low and suddenly 9500 strike delta and vega are high. I am not comparing. But I just want to know the technicality how it works.
Thank you
Hmm, this is option behaviour. For instance look at the volatility smile plot, the ATM vol will always be lower compared to OTM and ITM. While the vol itself may shift upwards or downwards making the ATM vol higher, but relatively, the ATM vol will always be lower compared to OTM and ITM.
theta is gradually reducing for all the higher strikes moving from OTM to far OTM. But how come delta, theta and vega are high for 9300 strike than 9250 and also theta and vega are high for 9500 than the lower two strikes 9450 and 9400?
Chandra, one should not compare the behaviour of greeks and expect a similarity between them. They all are independent variables, they all have their own influence on the option premium.
Hii sir ; I understand ( intrinsic value and time value Their formula ) but little bit confusion .
What time it is for us.?
Sorry, I\’m not sure what you mean by that 🙂
Hi Mr. Karthik,
theta decay with number of days is mentioned here, can you also say theta decay at OTM, ITM and ATM and how it will react at those three with number of days and I found today 9300 has less theta value than 9500 in 23rd april expiry. Is there any link btw theta, OI and volume?
Thank you
No direct link between theta, OI and volume as such. But yeah, theta decay is the highest for OTM, ATM and ITM, in the same order.
Pls explain theta vs time for expiration w.r.t ITM,OTM & ATM options
Hmm, they all decay with respect to time. The decay rate is fastest from OTM, then ATM, and then ITM.
Thanks for reply. I got that part but again a simple or silly question …..Being Option Seller I got my Premium…Then Why I would worry now if Premium reduces rapidly or not.
You get the premium but that will be entirely yours only when the options goto 0. Else you may have to buy it back at higher prices, which means a loss for the option writer.
Sir
1. What is the basis of deciding the lot size of a derivative ?
2. From last few years, I am seeing that lot sizes of many derivates changed (e.g. PNB from 7000 to 3500) but there is no change in the lot size of Nifty, why is it so?
3. Does the no change in the lot size of Nifty implies that Nifty is difficult to manipulate?
4. Does lot size has any relationship with the liquidity of the derivative ?
Thanks
1) This is at the exchange discretion. However, then try to ensure all contracts are of uniform contract values i.e. around 8L
2) Exchange reviews this once quarter and they change only if the contract value has drastically changed
3) Nope, that has no relationship
4) Not really
You mentioned \”You can sell options closer to the expiry – you will get a lower premium but the drop in premium is high, which is advantageous to the options seller.\” Can you please explain this? May be novice question but it will clear my confusion.
Thanks!
Viral Shah
Viral, as an option seller, I need to ensure the premium of the option drops rapidly. The change of this happening is quite during the end of the expiry (theta decay). Hence if at all someone wants to write an option, its probably a good idea to write towards the end of the expiry.
Hello sir,
Can you please help to explain theta vs time for expiration.
If I am a intraday trader so what will effect the premium more is it delta or theta. If the expiry is after one week.
Thank you
As the time to expiry shrinks, theta increases. Which means the premium decay also increases.
Dear Karthik,
The whole materials in Varsity is a great collection of knowledge, no doubt, as most of the others have acknowledged. I am relatively new to learning trading. I also echo the same. You, along with your team, are doing great service for people like me. Like somebody had suggested earlier, I also feel that while the large number of comments are definitely adding value to the contents by way of more clarifications, many a times, I find similar questions are being asked. If such duplications are removed, it will help new users save their time rather than skimming thru the repetitive stuff. I know it involves lot of effort, just a suggestion
Thanks for the suggestion Easwar. We are trying to figure a workaround for this. Will fix this going forward.
That\’s my mistake. Referred to some previous materials. I stand corrected.
No problem. Thanks.
In the example given by you, the intrinsic value is taken as SPOT – STRIKE.
Is it not required to multiply the difference with delta to arrive at the intrinsic value?
Delta in this case may be 0.6 since it is slightly ITM. So is it not appropriate to calculate the intrinsic value as 0.6 * 64.5 ?
Spot Value = 8514.5
Strike = 8450 CE
Status = ITM
Premium = 160
Today’s date = 7th July 2015
Expiry = 30th July 2015
Intrinsic value of call option – Spot Price – Strike Price i.e 8514.5 – 8450 = 64.5 We know – Premium = Time value + Intrinsic value 160 = Time Value + 64.5 This implies the Time value = 160 – 64.5 = 95.5 Hence out of the total premium of Rs.160, traders are paying 64.5 towards intrinsic value and 95.5 towards the time value. You can repeat the calculation for all options (both calls and puts) and decompose the premium into the Time value and intrinsic value.
Why do you think its necessary to multiply the difference with delta?
How can we calculate value of theta?
You get it from any B&S options calculator.
hi dear i want to ask if a sell a option with enough time to expire
for example : on 15th march 2020 nifty spot price is 8100 and i sell 10000 pe of nifty April month expiry at 150. what will be the effect of theta on the option and what will happen if the market trend changes from downward to upward.
Rachna, 10000 PE is a deep ITM option, you may not want to consider writing this. The effect of theta is the lowest for deep ITM options.
Hi Karthik,
I am Dr Ashok. I am new to futures and options (did value share trading for 2-3 years). I started reading about these topics on your varsity app in the last 1 month. This is an eye opener and you have tried to present the topics in a very simple way and even a doctor can easily grasp many practical tips from your chapters.
I congratulate you for your efforts to bring out such an app. It will help many people like me and others who believe there is no logic or science behind trading in share market. In India many people believe trading in the share market is gambling, and your app may change this attitude. I would like to congratulate you once again and thank you for bringing out this wonderful app.
Ashok
9945477554
Thanks for the kind words, Doc. Credit goes to the team who developed the app 🙂
[…] 14. Theta […]
But level 3 data cannot be accessed through kite python api sir. I am looking for an algorithmic approach sir.
Yes, you are right, Mani. It is not available as an API.
Yes sir, I have tried IOC orders. For now I have decided to stick with futures. I am also good at python programming, is there any algorithmic way to get orders filled at desired price sir? by looking at the depth or something like that sir
Hmm, you can use the level 3 data for this, that will help I guess. Check this – https://zerodha.com/z-connect/featured/introducing-20-depth-or-level-3-data-beta-on-kite
Changing market orders to limit orders did not work sir. Sometimes market moves fast, I even tried a combination of market and limit order sir. It did not work sir. Since only system or mechanical trading works for me, placing these orders and getting a fill is like discretionary and it drives me crazy sir.
There is one issue in directional option writing sir. I am trading the system after backtesting from 2009 to 2016 sir. From my backtesting and live trading data, my average points per year is 1000 sir. On an average there is atleast one 500 points trade per year sir. So if I were to write ATM option then my profits of that big trade will be limited to the premium sir.
How to solve this sir, like I have to close the current position and roll to current ATM option if the market moves 100 points in my direction, or roll to current ATM if theta increases to some value?
what is your suggestion? Is there any other way sir?
Mani, I agree about the fill part. I\’m sure you\’ve even tried IOC orders. Writing ATM options can be tricky, I\’d be a bit hesitant to do that. It is far safer to write OTM options, collect smaller premium, but write higher quantity…this lets you sleep at night 🙂
I am trading two trend following system on Nifty for past 3 years sir.
SYS1 – max holding time: 16 days
SYS2 – max holding time: 33 days
these two systems has given good results so far sir, now my futures lot size is increased to 25 lots sir. Because of this lot size slippage has become high, last year i have lost nearly 25% of profit to slippage sir. Also according to my money management plan I compound my the profits by increasing the lot size sir.
Option spreads are not viable sir because my system is based on trailing stoploss sir.
Due these reasons I have come to a conclusion that futures is not going to work for me in the long run sir. I am in a dilemma whether to do directional option buying or directional optional writing.
Hope you get some kind of idea from above points sir.So what is your suggestion sir?
Mani, slippage is a real issue given the liquidity of our markets. You may want to replace your market orders to limit if your strategy permits. If I were to pick one, I\’d select options writing with a directional view.
Hello sir, if wanted to buy naked options instead of futures is ITM best options sir? how many strikes away from ATM i should buy to protect from decay?
Mani, options should not be treated as a proxy for a future. A futures contract is impacted by just the directional movement of the underlying, whereas the option has multiple factors affecting this. So unless you are very clear about this, you should not think of replacing one for the other. However, yes, you can use the option as a proxy for futures by buying any deep ITM option. Deep ITM CE works as long futures and Deep ITM PE works as a short future.
Hi kartik,
Is there any change in theta? like change in delta is gamma!!!!!!!!!!!!!!!
Yes, changes with the passage of time.
Hello Karthik
You said at the end of the chapter that it is best to sell options closer to expiry. But wouldn’t it be better to sell it during the start of the series, pocket high premium, retain it till the end of the series and buy it back then, benefitting from the high decay and making higher profits than what one would have made through your strategy?
It is all about how much risk and volatility you can digest. Writing options at the start comes at a cost, higher premium and higher vol.
Sorry but I didn\’t get it.
let it clear by e.g so,
for eg. I have NIfty cmp 12230
put strike price 12000 and Ltp 60
expiry date 30jan
iv 12.06
theta value in decimal is 1.5795
then, what should be calculation to find theta value in rs.?
This means, all else equal on a daily basis, the premium will erode Rs.1.5795/- in value, attributed to theta.
How can we convert theta value from decimal to theta value in rupee?
Treat the theta value as the Rupee value.
sir, I forgot to thank you as I work at an Algo trading firm when I went there for interview for I was tested on stats, programming and options knowledge I was able to answer question-related to options as I covered both your modules on option which gave me great confidence with options knowledge and recently created an automated trading strategy for my firm on options .great thanks to u for providing such good content that enhanced my knowledge on options I have also pointed everyone who wants to learn options at firm to varsity keep up the good work sir.
Wow! Congrats on that, Sahil and thanks so much for letting me know. It feels good 🙂
sir, I want to trade stock options how can I find which stock options have a fair enough liquidity to trade them I want to know stocks options which maintain fair enough liquidity to trade year around not just on news or some events when their liquidity occasionally rise it would be great if u could point me out to a resource
Best to stick to the top 10 Nifty names, Sahil. They have the highest liquidity in stock options.
Hello, are greeks used in intraday options trading ? Or i can trade options with analyzing the stock price and getting in and out as stock chart shows signals to enter and exit?
Sahil, it does. Delta, Theta, and Vega all play an equally important role for intraday trading as well.
Hi Kartik,
I have one question.
Why Theta values are different for different strike price in option chain.
For Example 11800 CE AND 11900 CE should have same Theta as both are going to expire after 2 days. Then Why they are different.
What affects the Theta in short.
While theta is mainly a function of time, it is also dependent on the delta of the strike. Hence different values.
Sir how to select strike price please give example with delta or any other factors
Please help me …
Thats explained later in the module, suggest you read through Manoj.
Hi sir Theta value shows in bank nifty in sensibull is (ex 26400) -12.6 put option what is this meaning every day I loss -12.6 rupees for 20 lots x12.6= 252 or per lot 12.6? Which one correct..
Thats right Manoj. All else equal, you\’ll lose 12.6 by virtue of time decay. However, there are other factors (greeks) at play while trading options which tends to affect the premium. Hence you may not experience the theta decay on a Rupee to Rupee basis.
Hi sir Theta value shows in bank nifty in sensibull is (ex 26400) -12.6 put option what is this meaning every day I loss -12.6 rupees for 20 lots x12.6= 252 or per lot 12.6?
if increase delta what happened in theta
Yes, all else equal, the premium will erode owing to theta (theta decay). But in realist, other greeks kick in (like the Delta factor you spoke about), and therefore the premium erosion won\’t reflect as much as expected.
Hi,
Sorry if I am reposting the question.
Why is that Theta is highest at the ATM and goes lower at OTM/ITM and lowest at Deep OTM/Deep ITM?
Theta is option price sensitivity wrt time. As time passes, the chances that ATM converts to ITM or OTM is high, i.e. Chances you make or lose money is high. Deep ITM or OTM options are unlikely to change status wrt time, hence time has little effect on their premiums
Theta value depends on no.of days required for expiry, but I observed that in day theta value is keep changing. How?
If it depends on no. of days then it should change once in a day. please help me to understand.
It depends on the time to expiry, Pankaj. Think of it in terms of hours to expiry rather than days to expiry.
Hi Sir,
1. if theta increase faster towards he expiry, then how to calculate that? as it would be at one value during trade initiation and later at some other value.
2.is there any thing for theta like as gamma for delta ?
3. Why is theta value increase near towards the expiry?
1) Theta accelerates towards the expiry, this is a fact. So your trades have to be based on this assumption.
2) Meaning?
3) Theta is a function of time, which is dependent on the time to expiry. So lesser the time to expiry, higher is the theta decay and vice versa.
If I sell deep OTM option and on expiry date also the option is OTM. Do I need to square off my position or can be left like that and finale settlement will be done by exchange after market hours
No, not really. The option will expire worthless and you can retain the entire premium.
Thank you Karthik, your articles are really helpful and easy to understand
Happy to note that, happy reading 🙂
Sir what does all else statement indicate here.
Sir, if i buy ITM call of banknifty of 2nd month expiry and sell OTM of current month nifty call..Is it viable to trade to get profit at the end of month……how much time decay
affect….
Also if i apply in weekly basis example . buy ITM call monthly expiry of banknifty and sell OTM call of weekly nifty …..This i do sell every weekly nifty sell call . and closed trade at end…….
is it good pair trade to make trade in profit……or time decay loose me
Bipin, this is a calendar spread using option. The profitability really depends on many factors and can\’t really comment on it. Yes, you will benefit from time decay, but the final profitability depends on how other greeks behave.
Sir,
What is the effect of Theta of ITM Call options? Suppose if i sell ITM call options, will the value of ITM CE will decay with the passage of time?
Yes, all options tend to decay with time. ITM option may decay slower than OTM. However, why are you thinking of selling ITM options? It is a risky affair.
Thinking of ITM covered calls. Buying stock futures and selling ITM CE. , where the you will get a more protection. Please advice.
Hmmm, selling ITM CE can be tricky, Shekar. But I guess this is still ok, as it is covered.
Thanks!
Sir, I didn\’t quite understand. Let me rephrase:
What are the advantages and disadvantages to the option seller if:
a. he sells options at the start of series?
b. he sells options at expiry?
I understand the time factor and premium falling in accordance with that part but I don\’t understand the other bit.
Start of the series means there are more days to expiry. For example, expiry is on 27th of the month, and if you sell around 2nd or 3rd, its considered start of the series. At expiry means selling on 27th.
Sir,
I don\’t understand the following:
1. When you short naked options at the start of the series you can pocket a large time value but the fall in premium owing to time is low
Why is \”\’fall in premium owing to time is low\’ not advantageous to option seller? I understand the time factor bit.
2.When you short option close to expiry the premium is low (thanks to time value) but the fall in premium is rapid
Why is \”fall in premium is rapid\’ beneficial to option seller?
Please explain as I am new to this.
Thanks a lot!
The \”fall in premium owing to time is low\” is with reference to the initial part of the series. As you progress in time, the fall accentuates. This is also evident with the time decay graph. This should give you an explanation for both the questions.
Kartik Sir, please clarify when you can..
Hi Karthik,
As always, let me start by thanking your impeccable and selfless work. You are awesome.
Inspired by you, I was trying to build a checklist for my options trading. I have tried to make one. If you have 2 mins to spare, Kindly let me know if it is robust.
Initiate purchases of Just OTM options either CE/PE. The prior trend of the underlying should be directional (Up/Down). The trend should be confirmed by at least 7 to 8 candles on closing basis at EOD
The strategy is based on contrary approach. If the prior trend as confirmed by last 7 to 8 candles is Up, initiate purchase of Just OTM PE (trying to cash upon profit booking at higher levels which might drag the underlying down). If the prior trend as confirmed by the last 7 to 8 candles is Down, initiate purchase of Just OTM CE (trying to cash upon value buying which might propel the underlying Northward). This check has to be seen in conjunction with any of the indicators for concurrence. (Either Moving averages of 20, 50,100,200 days, (or) Bollinger bands, (or) Fibonacci retracement levels, (or) Pivot points (or) Double/triple-bottom/top on vanilla charts). Having initiated a purchase, always trade with stoploss.
Check for a recognizable pattern. Highly reliable ones by the EOD are: Double/Triple bottom for Uptrend. Double/Triple top for downtrend. Hammer at the bottom of a downtrend in order to initiate long position, Inverted hammer at the end of an uptrend in order to create short position. All the data shall be checked at the EOD on closing basis
Trade with more decisiveness if the indicators like Moving averages, Fibonacci retracement, Pivot points, long-term support or resistance are confirming the entry levels.
Limit purchases to first 2 weeks of a series. If trading opportunity pops out in the last two weeks of series, purchases shall not be done as the time value decays very fast, eroding the premium. However if the opportunity arises in the third and fourth weeks of a series, purchases can be done for the next series.
Having initiated a position, continuously trail the stop loss once the underlying starts moving in the intended direction.
Thanking you in advance
Regards,
Kiranraj
Hey Kiran, thanks for the kind words. I like the fact that you\’ve combined TA with options. The overall process appears to be alright, however, I have a feeling your longer term MAs may not confirm the trade as they are slow (even if you take EMA). I\’m also worried since it is against the trend, but this may just work well, but how will you backtest this? I\’m guessing you will have to manually track for opportunities, paper trade this for few weeks before jumping in.
Good luck!
Thank you Karthik. Yes, there is no way to backtest this as you said. I will have to manually track for opportunities. When I say underlying, I limit myself to Nifty50 or Bank nifty. I am not being stock specific. I believe no Index moves only in a particular direction (North/South) even if the long term sentiment is extremely directional. I am trying to cash in on the short term trend reversals (profit booking/bulls getting exhausted/value buying/bears getting exhausted) with considerably large volumes. As I limit my purchases to only Just OTM options, I believe they stand a good chance of ending up ATM or ITM even in a short term trend reversal (say for one or two trading sessions). I\’d hold my positions as long as the short term trend is in line with my directional view, square them off once it starts moving in adverse direction. If the trade goes wrong, My stoploss will square them off before they end up extremely OTM. Am i making any sense ? Or Am i just taking a gamble ?
Please confirm if my understanding is correct-
1. At a spot of 1000 and strike price of 1100CE, an option is valued Rs. 120 with delta 0.5 and theta 25. Now if tomorrow I buy at the same price say 120, for me to be profitable on the same day- the underlying should move atleast 51 points for me to be profitable?
How I calculated this. With 25 theta decay, option will anyway go to 95 even if zero move, then it must move at least (120-95)/0.5delta= 50 points + 1 point profit.
1) Think of this as buying a stock at 120 – you will be profitable the moment it crosses 120 right? Likewise with option premium. Now, given the fact that the delta is 0.5, this implies for every 10 points move in the underlying, your premium will move 5 points. Hence for a 50 points move in the underlying, you will make 25 points and your premium is like to hover around 145 (assuming all else equal).
The theta is best looked at an EOD basis and not during the day.
\’The theta is best looked at an EOD basis..\’
Considering everything constant after the 50 point move and premium coming up to 145, it\’ll still decay 25 points because of theta by the EOD, right?
It wont be a constant, Chirag. If the assumption is that all else is equal, then the upmove should not be considered.
Intrinsic value of a call option – Spot Price – Strike Price i.e 8531 – 8600 = 0 (since it’s a negative value) We know – Premium = Time value + Intrinsic value 99.4 = Time Value + 0 This implies Time value = 99.4.Sir how did you get 99.40 as intrinsic value? As the intrinsinc value is zero by formula? Can you clarify this?
Akshay, if an option has a Rupee value but the option does not have an intrinsic value, that means to say that the option\’s value is based purely on the time value.
I predicted that only but i thought you calculated that value.
Ah no, there is a formula to it.
Hi Karthik,
Do correct me if i am wrong, but i don\’t think the option premium is just the time risk+intrinsic val.
The time to expiry for all options is the same…so of we go by the above norm…once the option goes OTM…all options (just otm, deep otm) should have the same val…which is not the case.
I think the OTM premiums factor in the probability of getting ITM and ITM premiums factors in the probability of getting OTM. (If this is correct, then why do we follow the BS Model that only includes time & intrinsic val)
Also, if theta decay is reflected the next day…then on what basis the OTM premiums lose value on the day of expiry…that would mean theta decay cannot be reflected in next day opening price…
Do let me kbow what you think…thanks!
Alok
Do correct me if i am wrong, but i don’t think the option premium is just the time risk+intrinsic val —> Certainly not, the premium is also a reflection of the volatility as well.
The time to expiry for all options is the same…so of we go by the above norm…once the option goes OTM…all options (just otm, deep otm) should have the same val…which is not the case —- > how would account for this – RBI is coming out with monetary policy t\’row. The expectation on street is that they will cut rates. Going by your explanation, OTM bank nifty should just have time value right? But this wont be true, cause the probability of option moving from OTM to ITM is high.
Also, if theta decay is reflected the next day…then on what basis the OTM premiums lose value on the day of expiry…that would mean theta decay cannot be reflected in next day opening price… —-> But the decay actually happens on a continuous basis.
So this probability of change from OTM/ITM or vice versa is nothing but the Implied Volatility.. correct?
And thanks a lot for the quick reply…this will help me understand the Greek Calculator chapter better!😊
Volatility in a sense is the speed at which the market moves. Probability is more on the delta/vega side 🙂
Hi.. my question is, does theta reduce the option premium next day morning in opening price only or it gets amortized through out the day in some proportions?
For eg, if a option shows premium of rs15, and theta of rs1, does it mean the entire one rupee will be reduced in tomorrow morning\’s opening price ?
Hemin, technically speaking, with the passage of time, the theta reduces. It is a continuous affair, however, you will not really experience it as the absolute theta decay value is very small on an intraday basis.
Hi,
I want to understand if the theta decay during the day. If suppose the theta is -0.5 rs…so will this 0.5 be reduced gradually throughout the day…or depending on other fators…the tomorrow\’s opening will he 0.5 lower than yesterday\’s close! ..Thanks..
Technically, the theta decays with the passage of time. But the decay is quite small in absolute terms, hence traders don\’t really experience it (especially when there is ample time to expiry).
\”Theta is expressed in points lost per day when all other conditions remain the same. \”
I have a doubt on this.
For an OTM CE, If Theta is (-6) on Friday at 3:30pm, what does it portend for Monday opening prices (all other things remaining same)?
Will premium drop by Rs 18 or by Rs 6? Does the B&S model factor in time decay for non trading days while throwing up the value for Theta, or does it not ?
Sorry, pls ignore that question. I see it has been answered earlier.
I\’m glad you found the answer, good luck 🙂
Hi Karthik,
Is theta in effect during non trading sessions (weekends and public holidays) as well? i.e., does the premium erode because of theta in non trading sessions as well?
And also what about between sessions (Between 3:30pm current day and 9:00 AM next day)?
Yes, Vishal. There is an effect between sessions and weekends, but may not be tangible when there is ample time to expiry. The closer you move to expiry, the more tangible this is.
Sir,
If I have purchased 15 Lots of Nifty and paid Margin for it, what is the best time and Rate to hedge the position via buy a Put Option, I am Long term bullish on the market but want to hedge the position due to political uncertainty.
1. At the money ; 1st day of present series
2. At the money ; within 1st week of series
3. At the Money ; always midday of series
4. In the Money ; 1st day of present series
5. In the Money ; within 1st week of series
6. In the Money ; always midday of series
7. 1 strike Out of the Money ; 1st day
8. 1 strike Out of the Money ; within week
9. 1 strike out of the Money ; midday
Same 9-9 possibilities for near month and far month illiquid options
Thanks
Kindly give answer in detail for my problem and oblige
Darshan
Sir, but isn\’t it true that for a put option, sometimes the short term maturity put value is more than the long term maturity put value because of time value of money?
Especially when it comes to Deep-in-the money options?
I have raised this point because you said that all options are depreciating assets. I agree with call but with there is a caveat with put options. Please correct me if I am wrong?
Not really, Umer. All options depreciate in value over time. This is true for both call and Put options.
Hi Ranganth
Is it good to buy a call option in between the 3 rd week of the contract series?
Yes, as long as you have your thesis in place.
I think premium should be sum of intrinsic value and extrinsic value(implied volatility + Time value)..You just stated time value and ignored Implied volatility..If Implied volatility increases it will definetely increase premium..
Mayursinh, when we say time value, it includes implied volatility. Remember, implied volatility is one of the parameters of time value…or in other words, time value is a function of time to expiry, IV, Strike, and the option type. Most traders think time value is just attributable to time to expiry, in a sense its true, but it also includes other parameters.
Spot Price: 10630
Strike Price: 10700
Premium: 2.8
Delta: assuming 0.2( since it\’s OTM)
Now next day, big jump
Spot Price: 10730
Strike: 10700
Premium: (10730-10630)*0.20+2.8= 22.8
Question:
Since the premium is 22.8 and Intrinsic value is 30(10730-10700), is the whole premium attributable to intrinsic value and nothing to time value?
Yes, in fact, the premium will be 30 plus time value, so it will be more than 30.
That\’s great. It means if I hold a 26500CE BNF at 100 on Wednesday & I predict it closing around 26700 then my premium will definitely be 200+ on Thursday expiry
Yes.
this is the most easiest greek 🙂
Of course 🙂
If i sold deep otm put and it expires as otm then i will get the entire premium right??
Yes, you will.
Dear Karthik,
Say I have sold OTM Strike price Bank Nifty and its value becomes zero on expiry and remains OTM. Before it expires shall I have to buy the contract to complete the transaction or allow it to lapse at zero. What about the brokerage and tax and will the profit b credited to my a/c even though I allowed it to expire? Pl. Clarify
Yes, you can let the option expire worthlessly. No problem with it. You will get to retain the entire premium.
Thanks for lucid explanation.
Does theta changes w.r.t underlying spot price like delta or is it fixed?
Theta is reactive to time therefore changes only with respect to time.
hi sir,
its nice to read your article to get understand about theta, but still i have one basic confuse while placing order…
call options:-
1) if theta was 0, then we need to sell or
2)if theta pasitive we need to sell clarify me
1) Theta cannot be zero
2) You sell closer to expiry when the theta is decaying faster.
Does rate of premium on Friday 3:25pm be discounted for the two days theta decay.
All else equal, yes.
Dude, you are God! Love your teaching skills. Thank you so much for all this effort that you have put and continue to put into the teaching. Greatly appreciate your work.
Vidya
Lol 🙂
Thanks, Vidya! Glad you liked the content here. Happy learning 🙂
Nifty Spot = 10760
CE 10850 Premium = 83
CE 10900 premium = 65
Both intrinsic value is 0 but time value has a difference of 18 rs. How to arrive at this 83 and 65 rs time value ?
So like delta of atm options is always around 0.5 what is the formula for calculating time value ?
Have you tried the B&S calculator? Check this – https://zerodha.com/tools/black-scholes/
Yes I have used this calculator but it just provides the final calculation… I want to know how is the time value calculated (formula). Like if spot Nifty is 11010 so i can be sure that delta of CE 11000 will be around .53
So what will be the theta of an option if there are 5,10 or 15 days to expiry? Is there a formula to calculate that ??
That would involve 2rd order derivatives, I\’ll try and point to a source from where you can learn this.
Spot nifty 10760
I Buy Nifty CE 10750
Delta = 0.55 Premium = 131 Theta = 5.00
Premium = Int value + time value
= 10 + 121
All other things remaining constant, will the premium drop by 5 rs to 126 rs the next day ?
Yes, all else equal the option will be lesser by theta.
Is there any video blog for the same?
Not really, although we have some good educational content on our Youtube channel. Check this out – https://www.youtube.com/user/zerodhaonline
Sir after reading this chapter I checked out few of the charts and what I observed was that option premium has the highest value at the start of the contract (I\’m guessing due to time) and gradually decrease in value over time. So am I right in saying that if you are the option seller at the beginning of the contract you are always on the right side?
I\’d agree, however, if during the series the stock/index gains a lot of momentum then you could be in trouble doing this.
Hi Kartik
Sorry for taking the query regarding theta in the volatility group .What will be the percentage decay of the option on a daily basis daily supposing the underlying stays at at the money(theoretical) till the life of the option .Also is there any relation in percentage between daily volatility and theta percentage when underlying at the money? For eg if there were 20 days to expiry and at the money premium is 20 what will be the percentage decay on a daily basis.Will it be eroding the same percentage on a daily basis or rapid erosion on expiry and if not uniform the difference in percentage?
No problem, Najeeb. I answered it there as well.
If all else equal, the loss in option premium owing to time decay is equivalent to the theta of the option.
If the volatility increases, then the premiums also tend to increase. This is especially true when there us fewer days to expiry.
Karthik,
Just a suggestion on page navigation:
Its fairly easy to navigate to a different chapter in a module if I start reading from the top. However, its extremely difficult to get to module-navigation from bottom; one has to keep scrolling / pg-up repeatedly. This gets bothersome if you\’re trying to jump across different chapters / refresh your concepts that you can\’t recall etc.
I\’d like to suggest adding links at the very top + very bottom (right above the comment box) of the page to the table-of-contents for ease of navigation.
Great stuff! Keep up the good work.
Thanks for the suggestion, Rahul. Will share this with our tech team.
sir, i am confused
there should be increase in premium with increase in underlying,
suppose;
i am long on CE and the underlying price moves up in my favor and now i want to sqaureoff my position next day, what will happen?
will i lose money because of dercease in premium?
For long positions, as long as the premium is above your buy price you will make money. Likewise, when you sell (write) options as long as the premium is below your sell price you will profit.
Completed the first 10 chapters of this module..I have never found anything on options trading to be this simple and precisely explained before..hats off to you Sir..
Wishing you and your team the best of luck!!
Thanks for the encouraging words, Anu!
Hi,
All your modules are very informative! Kudos for this yet another initiative from zerodha!
I had one query regarding greeks I sold one lot of stock option on 27th Jun strike price was 740 and spot was 670! The premium recieved was 8.30 !
Today the spot is 745 and the premium is around 13!
1) Is it correct that my breakeven on expiry will be 748.3 (spot)
2) Would I recieve a higher premium if I would have sold the same stock option say strike price 750 today 4 days from expiry?
Thanks!
1) Your breakeven is 748.3 (assuming this is a call option)
2) Yes.
Respected Sir,
Keeping all else constant, when does Theta effect take place? Does premiums gradually decline during the trading session, or does the next day trading session open directly after specific deductions (equal to theta value) in premium prices, or both?
Thanks in advance !!!
Best Regards
James
The effect of theta starts from the time a contract comes into existence. However, the effect is not really felt by traders when the contract is young and early in the cycle. However, as the contract ages and approaches expiry, theta accelerates and the effect intensifies.
Sorry! I guess I couldn\’t make myself clear. I am new to option trading so curious about theta decay while market is closed. For example, option premium of XYZ on Monday was-
Open-11.20,
High – 14.27,
Low – 7.42,
Close – 8.42
Of course, theta contributed to drop in price from 14.27 to 7.42 during the Monday session. But,
Q.) What will be open price of premium on Tuesday (assuming all other factors remain same)? Will it be 8.42 (Monday\’s close) or something less due to theta effect?
Thanks & Regards
James
Theta could not have contributed to a drop from 14.27 to 7.42 – clearly delta is playing the prank here.
If the theta is 0.5, then all else equal, the premium will trade 0.5 less of 7.42.
Iam also new to options trading .. Just continuing James\’s question here..
Does time value decay of a option happen continuously throughout the day or during specific time of a day ( Like early in the morning or close of day ) ?
Also Appreciate the way you are writing and explaining..
Purely from a mathematical perspective, the theta decay happens on a continuous basis. However, you can experience the decay on an EOD basis (its more tangible this way).
Also is there time value decay during weekends and trading holidays ?
Thanks in advance
Yup, there is.
Hi Karthik
As mentioned above due to time decay premium decrease, but using Black and Schole Calc I found that for Deep ITM, PUT premium increases with time decay as the theta is +ve for deep ITM? How is it possible??
Can you Please explain. It means if we go long on Deep ITM Put then time decay will favour Long postions considering market remains static(value doesn\’t change)??
In general theta has a -ve effect on options premium. However, yes, deep ITMs premium do tend increase as the probability of deep ITM remaining ITM increases as time to expiry decreases. This can however, be attributed to deeper deltas.
Dear karthika
Thanks for your guidance that helped me to pick up the nitty-gritty of Options.Please clarify my following doubts:
1.If I shift my broker to zerodha will my current holdings be transferred. If yes what is the method.
2. Since OTM options have IV of zero, and delta affects only IV , so how does delta really affects an OTM option.
1) Yes, you can transfer your portfolio (holdings) from your existing broker to Zerodha. Check this – https://tradingqna.com/t/how-do-we-transfer-shares-from-one-demat-account-to-another/70
2) Delta affects the premium, does not matter if its ITM or OTM.
Dear Karthik
Thanks for the guidance . Pls clarify my one more doubt:
How is intrinsic value related to delta. Does it follow the same pattern as premium vs delta.
Delta is one of the forces which has an impact on IV along with other greeks like vega, theta, and gamma.
Dear Karthik
I was looking into NIFTY Option chain on 15.05.2017 for CE @stricke price of 8600 at a premium of 846.55 with NIFT spot at 9456.15. It indicates intrinsic value of 856.15 and hence a time value of -9.6. Is it possible. The expiry month is near month.
Time value here is almost zero. Also, remember trades in deep ITM or OTM option will be few, hence liquidity is lesser, and therefore the premiums may not be priced right.
Hi karthik sir,
I want your opinion here. What do you say about STRIKE VS TIME VALUE
For an ATM option the time value\’s share in premium is maximum and we move to ITM from ATM or to OTM from ATM. The time value starts decreasing and forms a chart like gama (the bell looking) chart
i always thinks that we should not buy optiïon when there is just 10 to 14 days left in expiry because in normal days the movement in underlying stays close to its AVERAGE and THETA beats the DELTA and you always end with lose due to theta
But now with this BELL curve of time value vs strike we can consider buying in ITM and OTM if we have predicted that underlying will move in a meaning full manner and with this we can expect almost same gain as in starting of series where theta is lowest
I mean in above case the decrease is premium will be lower due to THETA campare to increasing in premium due to DELTA if there is noticiable DELTA
if i am doing this trade i wil get out of the trde before expiry for OTM as it has to be ZERO at expiry
So, what do you say is this right thing to do….??????
Yes, you can. In fact, when you are convinced about the directional movement, the best option always is to buy options….especially when you also have time working in your favor. Also remember, the effect of Theta starts to forcefully kick in towards the end of the series….maybe when there are 5 days to expiry or last week of expiry. Take up the trade if you are convinced, but square off before expiry.
Okay sir,
Take this example(imagined not real) of CALL OPTION
Spot 400
Strike 370
9 days to expiry
Status – DEEP ITM
Premium 25
Sir my question is if we playing a ITM OPTION
Then that option must have positive intrinsic value and positive time value
Say atlest 5 or 7 or 10 or whatever you say for time value
Intrinsic value = spot-strike=400-370=30 right
Then premium must be more than 30 for above case
But instead of >30 it is at 25
This driving me to this formula
Premium = (spot-strike)+time value
25=(400-370)+time value
Time value= 25-30=-5
Is this suggests the time value is in minus (i think not possible)
Premium must have ZERO or a positive mon ZERO NUMBER FOR both its content.
Sir this is really happend i was considering a stock option few days ago
Where ITM option premium was different from what we have knows…….
Thanks sir…..
In the example quoted above, the option price must be at least 30 (int value). Anything lesser than that is an aberration and will get sucked up by the markets soon. Its highly unlikely that you will come across such situations. If you do, you need to buy the option and wait for the premium prices to reflect the right price.
Hello sir,
I tried it but did not get results
Ex:- For Otm (CE)options if premium is at 8 then, as per formula
Time value =premium-intrinsic value
Since,intrinsic value is 0 for OTM so, all the premium is for time value
BUT in case of ITM option where premium contains Non zero number for
both Intrinsic and time Premium not maching with formula i saw in many strikes the ITM\’s time value coming in MINUS NUMBER
EX:-
PREMIUM= Intrinsic+time
35=40(int value) + time value
Time value =35-40 =-5
what this suggests is premium drop for time is more than is should be???????
ITM options contains high Int value and low time value. I\’m a little confused on what you are trying to calculated. Can you please explain this again for me, please. Thanks.
Sir,
Sir is ITM and OTM contains little time value if yes
Then is there a way how to calculate that time value
Simply i want to ask how to seperate ITM\’s time value and intrinsic value
You can use this basic formula – Premium = Intrinsic value + Time value.
Sir, minimum sip in most of mf is 5000, i wanted to start with 1000 in kotak select focus, is their any way ?
You can, only the first transaction will be for 5K..but you can continue with 1K every month.
Thanks for clarification
Cheers.
Hi karthik sir
Sir what is RHO is this also a topic in this module
Rho is an option greek which measures the sensitivity of the premium with respect to change in interest rate. Since interest rates dont change often, we have just omitted this greek.
Hi Karthik,
Hope you are doing great!
I am a newbie in markets and after reading this i started fantasying about making money buy selling both call and put for a strike price. Assuming that there wont be any effect of directional movement on this kind of position, As time will pass (let say a week) the total value of the option will decrease due to time decay and we can lock in the profits by buying them. is it feasible or i am missing something because everyone can think of this strategy. Please enlighten me on this. Thank you
Yes, its doable as long as you write the right strike and have the appetite for risk.
Hi Karthik,
Thanks for replying, Could please put more light on choosing right strike?
Thanks
The whole of this module is dedicated to that 🙂
Hey Karthik,
You said an option is depreciating asset and premium erodes daily. I can understand this for call option where strike price is greater than spot price. But what about when strike price is lower than spot price already? i.e. ITM
Spot – 8000
Strike – 7700
Premium – 100
Wouldn\’t premium will increase in this case as time passes? Call seller is almost certain to lose premium.
If spot is at 8000 then the premium for 7700 CE would be at least 300. If there is ample time to expiry..then the premium will be more than 300…if nothing else changes, then the portion over and above 300 will erode as time passes. This is mainly attributable to time decay.
Hi Karthik,
As mentioned in the chapter , the Intrinsic value can never be zero.
For a call CE option the Intrinsic Value (IV) is calculated as \”Spot price – Strike price\”.
But if we see on the option chain of Ashok Leyland on the link
https://www.nseindia.com/live_market/dynaContent/live_watch/option_chain/optionKeys.jsp?symbolCode=228&symbol=ASHOKLEY&symbol=ASHOKLEY&instrument=-&date=-&segmentLink=17&symbolCount=2&segmentLink=17
the IV column has some high numbers which are not \”Spot price – Strike price\”.
Can you please let me know what these numbers are in IV column?
Thanks,
Rishikesh
The intrinsic value can never be below zero….however, it can be zero. The IV that you see in the option chain is \’Implied Volatility\’ and not the intrinsic value 🙂
Thanks for the reply. So under what conditions, time value can go negative before the expiry?
Thanks a lot on advance.
Cant really go to -ve. It terminates at 0.
Thanks. But in the example above, I have shown the calculation that time value is negative for a call option. Kindly explain how is that possible. Data is taken from NSE website.
The -ve sign just indicates that the value is a depreciating one. Think about it, options expire on expiry day…given this the least the TV can go is 0 because on expiry day the contract ceases to exist.
Dear Sir,
How can time value for a call option be negative when there are still 2 weeks left for expiry? Please see below example I took from NSE website today, i.e. 12th Aug 2016:
Spot price – 365.55
Option type – Call option
Strike price – 320 (ITM)
Premium price (Call Option) – 29.5
Derived Intrinsic value = 365.55 – 320 = 45.55
Time risk value of option = Premium minus Intrinsic value = 29.5 – 45.55 = (16.05)
Please explain the rationality of such premium pricing. Can there be any trading opportunity in above?
Thanks
This is because options are considered a depreciating asset and it depreciates with the passage of time as time moves only in one direction.
Thanks sir for the reply.
Does that mean that time value of the option can go negative even if there are two weeks left for expiry? My understanding is that time value of an option will depreciate towards zero(it should not go below zero) as expiry time approaches.
Please clear my understanding.
Thanks a lot in advance.
Yes, TV depreciates from a positive value all the way to 0 in such a way that it coincides to 0 on the day of expiry (at 3:30PM).
\”Time moves in a single direction hence Theta is a positive number.\”
\”Theta is a friendly Greek to option sellers.\”
I can\’t relate any point here. Being Theta +ve, why do we take -ve value for Theta in a long position to calculate premium depending upon expiry.
You have shown examples while selling option. Can you please elaborate the same with a buying option as
1. Buying Call; Market is rising and Days are expiring, but the premium is rising.
2. Buying Put; Market is falling and Days are expiring, but the premium is rising
Example : Theta of +0.2 implies that the premium erodes 0.2 points on a daily basis till we hit expiry…this is assuming all else equal.
1 & 2) This is because of increase in delta or maybe volatility. The same explanation holds true for both the cases you mentioned.
Thanks, Karthik
So for buyer theta effects in negative direction rather making the profit and for the seller, theta helps to be in profit.
Is my assumption correct?
Absolutely!!
Dear karthik sir,
I have a question….assume that i am selling 8500ce @ 20rs. And spot is 8200 before 5 days of expiry and on expiry day nifty comes upto 8450 spot and premium becomes 30rs somehow…so still 8500ce is otm…so will get 30rs. Premium as profit or 20-30=10rs. Loss ???
If the expiry happens at 8450, then you will still get to retain the Rs.20 as profits. However if spot closes at 8510, then you will lose Rs.10…and if spot closes at 8520, you will not make anything…and anything above 8520 is a loss for you.
Thanks for reply sir…
How can I pull the values of greeks in Pi, I remember this was available in Nest Trader. You could also provide the same in kite, maybe a separate page also support for entering option leg orders..
Its not possible on Pi for now, but we are sketching details for Kite.
Does Theta play a role when I buy say after 3:00 and sell tomorrow. Or it decays over the day?
It does, especially when you are closer to expiry.
Dear Sir,
Using the black scholes model what\’s the formula for calculating the Delta, Gamma, Theta, Vega and Rho. Even at zerodha site there is a Black scholes calculater were i have found the values of Delta, Gamma, Theta, Vega & Rho. How have u arrived at this values. Just need the formula to calculate it in excel.
Sonjoe Joseph
Here you go – https://en.wikipedia.org/wiki/Black%E2%80%93Scholes_model
Thanks Kathik….
In my previous calculations, I think there is some error in second one when spot goes down by -10
new premium=5.75 -10(.401) -10(-.207)= 1.74 +2.07 = 3.81
here premium is increasing with theta(-10*-.207=+2.07)
how come?
Here is the general framework Rohan – For a call option with increase in spot price/time/volatility, the delta increases hence adds to premium, time value decreases hence drags down the premium, and with increase in vega the premium increases.
For a put option with decrease in spot price/volatility, the delta increases hence adds to premium, with increase in vega the premium increases. Time moves in only 1 direction hence it always tends to drag the premium lower.
Can you explain how decrease in volatility increases the delta of a put option. I am of the opinion, decrease in volatility decreases the option premium of either put/call option.
Can you please share the link where I\’ve mentioned this? Yes, volatility and premium are linearly related.
In the above comment to Rohan you mentioned \”For a put option with decrease in spot price/volatility, the delta increases hence adds to premium, with increase in vega the premium increases. Time moves in only 1 direction hence it always tends to drag the premium lower.\”
I stand corrected, it should read \”For a put option with decrease in spot price, the delta increases hence adds to premium…..\”
wipro
spot-559
strike-580
580CE
Premium-5.75
delta=.401,gamma-=0079,theta=-.207
if spot moves 10 points in 10 days the-
new premium= 5.75 + 10(.401) + 10(-.207)=9.76-2.07=7.69
if spot moves -10
new premium=5.75 -10(.401) -10(-.207)= 1.74 +2.07 = 3.81
my questions-
a) are my calculations of new premium correct?
b) when spot is moving down in call option theta is adding to premium . as spot =-10 and theta=-.207 so minus multiply by minus becomes plus.But it should not be the case as premium should decrease??
You also need to take into account Volatility (vega) which calculating new premium, but assuming volatility is constant your calculations are ok. Do remember, Theta always tend to eat away the premiums (hence good for option writers).
Sir, please provide option calculator as well as value of all Greeks at kite in live market that uses volatility from India vix. It will be very helpful to trader , at least for nifty and Bank Nifty.
Hopefully, something soon on these lines should be available.
Assume that I sell a call option at 8700 Strike Price(Jan expiry option) on Jan 1st 2016 at a premium of 80Rs (OTM) . Somehow nifty keeps falling goes towards 8300 and by the end of the expiry it only recovers and closes at 8500. Does this mean, I will retain the whole premium because it will eventually drop to 0Rs?
I am asking you because I want to know, if I am at thinking on the right path? Assuming the other thing remains constant.
Absolutely. 8700 CE will be In the Money only if upon expiry the spot is higher than the Strike. If the spot is lesser (like 8500 or so) then the option will not have any intrinsic value hence you get to retain the entire premium of Rs.80.
IS THETA A CONSTANT GREEK OR VARIABLE LIKE DELTA AND GAMMA
Theta increases as time progress, hence its not a constant.
how u control the operator who actually moves the LTP against ur all calculations,on increase of price he keeps the LTP not to change proportionally and u r put to loss what to do?
As long as you deal with highly liquid stocks like HUl, ITC, Reliance, Infy, Nifty etc you need not worry about any operator.
Hi Karthik,
I am keeping mum with the awful simplicity of the material. Chapter by chapter I am grasping details and structure of the options. I had started to trade in options thinking that those are easy and straight forward like futures. However, my calculations went wrong at the time of expiry. I didn\’t know all this background which I am referring. I cannot express my gratitude in words. You are great teacher. Keep imparting the knowledge. Thank you very much once again.
Thank you and I really hope you find all the other modules/chapters equally good. All the best and please do stay tuned on Zerodha Varsity.
Karthik you are a great teacher this chapter is an example how a good teacher can make esoteric topics look simple.
However, I feel the value of theta should be negative if it is taken as rate of change of premium with respect to time. It would be mathematically correct as well.
Thanks for the kind words Sunil. Theta is a -ve value, as it indicates the fact that premiums lose value as time passes (assuming all else constant).
Hey Karthik. The value of the premium = Intrinsic value + Time value. At any point, is it possible for Time value to be negative?
w.r.t the 7500 CE, the Premium is 790.7. This was as on Friday, where the spot was 8,299.95. So the intrinsic value is 799.95(8299.95-7500, which means the time value is -9.25(790.7-799.95)?
8299.95 – 7500 = 799.95 (this is the intrinsic value and the minimum option premium). The premium is 790.7 (maybe because its not liquid, hence the mis pricing). Time value is 0 and not -ve.
No, neither time value or intrinsic value can be -ve.
Hi Karthik,
All the chapters are very easy to understand and easy to relate with. I just have a small query. How to calculate the number of day to expiry. Do we need to add only the traded days or do need to add non traded days (Weekends) with traded days to get the total.
You can include the non traded days as well.
we are waiting for the next chapter , when will it come?
This week sometime.
Today Sun Ph is up by around 3 rs to 949/- but its CE 1000 has gone down 25.40 to 23.10 and pe1000 has gone up 22.45 to 28..05. Why it is so, not able to understand. See the copy paste below.
Previous LTP
close
30 Jul 2015 CE 1000.00 23.95 18.75 25.40 23.10 2518 6427.26 1040500 Jul 20 2015,11:32:00 AM
30 Jul 2015 PE 1000.00 31.60 24.00 22.45 28.05 672 1728.10 285000 Jul 20 2015,11:32:00 AM
Can you please explain this.
Thanks.
As I\’ve mentioned – option prices are not just affected by directional movement but lot of other variables. In this particular case, 1000 CE is OTM and 100PE is ITM…remember ITM options are more sensitive to price changes.
ya that is true, but the price has gone up so PE premium shall come down not go up. Including theta effect also PE/CE shall go down only if price movement is not dominating. For PE to go down there are two factors in favour: price going up and time decay. Which is the third factor which is dominating them?
Vega or Volatility. We have just put up a chapter on Volatility here – http://zerodha.com/varsity/chapter/understanding-volatility-part-1/
Hey Karthik, just saw your interview on MoneyControl.com. You should so have a discussion forum on Zerodha to discuss multibaggers, stock picks and the process of choosing multibaggers…the nitty gritties. It will be a valuable practical exercise in fundamentals for us.
Hi Vidya, glad you bothered to watch 🙂
Thanks for suggesting, may not be a bad idea. Will bounce this off internally 🙂
Karthik,
I think it would be a good idea to consolidate all the important questions that add to the context of the different chapters and create a separate page for the same. And if possible then remove the comments asking for \’when is the next one coming\’ from the comments of the previous chapters. While it seems beneficial to me to see what other folks are asking as questions, it is difficult to find the relevant questions pertaining to the corresponding chapters due to the above reason.
See if something can be done 🙂
Thanks for the suggestion Saurabh. Will try and do something about this. Cheers.
Thanks for the article Sir… 🙂
Welcome:)
Hello Karthik….
Thanks for info on theta….eagerly waiting for next chapters…
Very soon 🙂
HI Karthik,
How I can check theoretical value calculation of Call/Put options ,which give the exact value of Gamma/Delta/Theta
Option calculator does this job. We will discuss about the same very soon in this module.
Mistake at chapter 14.3:
A Theta of -0.5 indicates that the option premium will lose -0.5 points for every day that passes by. For example, if an option is trading at Rs.2.75/- with theta of -0.5 then it will trade at Rs.2.70/- the following day (provided other things are kept constant).
ACTUALLY THE NEXT DAY OPTIONS VALUE SHOULD BE 2.25 AND NOT 2.70
PLEASE RECTIFY THIS.
Thanks, guess I missed the \’0\’ in theta value…it should be 0.05!
Thank you for pointing this out. We have made the necessary corrections.
Karthik my question is:
Say I am an option seller (S1) who sells 1 contract of an OTM CE for 90 to an option buyer (B1). Three days later the option is still OTM and the premium drops to 80. Now If I square off my position. This means I am essentially closing the trade and transferring the risk of selling the option to somebody else (S2) with a profit of Rs.10. Let us say the person who bought the contract (B1) for 90 still holds it:
In this case:
1. S1 initially received Rs.90 from B1
2. Three days later S1 closed the position and the contract was automatically transferred to S2 for a premium of Rs.80
Now say the option becomes ITM and costs Rs. 120 on day 4 and buyer B1 closes his position and the contract gets transferred to B2.
In such cases where people square off on the basis of premium changes – who is the final owner and which seller finally pays if the premium rises? Would S1 be involved or would S2 pay for the premium rise from 80 to 120 to B1?
Saurabh – your thought process is correct, in fact most of the option trading is a play on premiums. In fact this point will strongly emerge towards the end of the module. The final owner and the seller will the those who hold on to the contract on the settlement day. So for example Nifty 8400 contract can be bought and sold by many traders during expiry…but the final set of traders who own (either bought or sold) matter for settlement.
Hope I\’m not confusing you with that 🙂
Nope – I expected just that – I just wanted to confirm – sounds pretty simple and straightforward – All thanks to the simple way in which things have been put here 🙂
Good luck Saurabh 🙂
Intrinsic value of call option –
Spot Price – Strike Price i.e 8514.5 – 8450 = 64.5 (since it’s a negative value)
In the above text I think the \”(since it’s a negative value)\” is a copy and paste error. as the IV is 64.5 a non zero value. Please clarify.
Thanks
Thank you for pointing this out. We have made the necessary corrections.
Hi kartik,
Thanks for this wonderful chapter. In one reading I almost understand the concept of chapter. it\’s contents are very clear and easy.
Everyday I closes my position my position before 3:20 p.m. so I think theta will not effect my trade as decline in price occurs on everyday basis. Please correct if am wrong.
Theta does not play a big role when it comes to intraday trading. However the effect of theta is high just around expiry…so please be aware of this.
Sir,
Again it is very simple and crisp explanation. Thanks.
Is the theta value is same for all stocks keeping all other factors same? What u have shown is drop in the premium verses time. What will be the theta value verses time? I believe that it will change inversely and exponentially with time.
Theta is friend for the seller is well understood, so if we sell a deep OTM option so that the probability of its expiring worthless is more and to pocket the premium at the expiry, may be a safe deal?
Theta varies stock to stock, but certainly behaves the same for all stocks and indexes. In fact theta increases as we process in time…so less time to expiry, the more the theta, hence more the drop in premium, by virtue of time. You are absolutely bang on the money regarding OTM options.
selling a deep OTM option is fine. But the question is will get the buyer for the deep OTM option?? I am novice in options. havent traded yet. Just aski
selling a deep OTM option is fine. But the question is will get the buyer for the deep OTM option?? I am novice in options.,havent traded in options yet. Just asking based on ur experience..
You do, at least in Nifty and few stocks.
snapshot 2 and 3 are interchanged!
Got it fixed Ramesh. Thanks!
Whether theta will help in intraday trading if I short delta neutral deep OTM options..
It does, like I said earlier the next module is all about Option strategies 🙂
Sir,
Pls explain theta vs time for expiration w.r.t ITM,OTM & ATM options
Amit, makes sense, not sure how I missed this…I\’ll probably make an addendum to this chapter.
Hi karthik,
I cannot still find above query ans in this chapter??
Its on the list of things to do, hopefully soon.
Hi,
The soon is still not arrived :-p
Can you please add it now
I understand, Abhijeet. I\’m dependent on someone else for the graphs, it is taking a bit of time.
Its been 3 years. How slow can your graph guy be?
What are you reffering to, Arjun?
Hi Karthik
Still this query has not been addressed .. I thing this will clear effect of theta . Waiting for replay
Which query, Gajanan? Can you kindly elaborate? Thanks.
Nitinji,
Its a bit confusing…so what u mean to say is :If i buy options at start of series,i would always lose money at the end of expiry due to theta…then when should one be a buyer of options?
Also,according to u,what is more profitable…futures or options?
Pankit – you missed one important line 🙂
\”All else equal then by virtue of time the premium value decreases on a daily basis\”. But in reality \”all else\” is not equal. So on hand if theda decreases premium value, delta or vega will increase the premium value. So it it very important to understand all the greeks and its cross dependencies. We will talk about it later in this module.