15.1 – Background
Having understood Delta, Gamma, and Theta, we are now at all set to explore one of the most interesting Option Greeks – The Vega. Vega, as most of you might have guessed is the rate of change of option premium concerning the change in volatility. But the question is – What is volatility? I have asked this question to quite a few traders, and the most common answer is “Volatility is the up-down movement of the stock market”. If you have a similar opinion on volatility, then it is about time we fixed that ☺.
So here is the agenda, I suppose this topic will spill over a few chapters –
- We will understand what volatility really means
- Understand how to measure volatility
- Practical Application of volatility
- Understand different types of volatility
- Understand Vega
So let’s get started.
15.2 – Moneyball
Have you watched this Hollywood movie called ‘Moneyball’? It’s a real-life story, Billy Beane – manager of a baseball team in the US. The movie is about Billy Beane and his young colleague, and how they leverage the power of statistics to identify relatively low profile but extremely talented baseball players. A method that was unheard of during his time, and a method that proved to be both innovative and disruptive.
You can watch the trailer of Moneyball here.
I love this movie, not just for Brad Pitt, but for the message it drives across on topics related to life and business. I will not get into the details now, however, let me draw some inspiration from the Moneyball method, to help explain volatility :).
The discussion below may appear unrelated to stock markets, but please don’t get discouraged. I can assure you that it is relevant and helps you relate better to the term ‘Volatility’.
Consider 2 batsmen and the number of runs they have scored over 6 consecutive matches –
| Match | Billy | Mike |
|---|---|---|
| 1 | 20 | 45 |
| 2 | 23 | 13 |
| 3 | 21 | 18 |
| 4 | 24 | 12 |
| 5 | 19 | 26 |
| 6 | 23 | 19 |
You are the captain of the team, and you need to choose either Billy or Mike for the 7th match. The batsman should be dependable – in the sense that the batsman you choose should be in a position to score at least 20 runs. Whom would you choose? From my experience, I have noticed that people approach this problem in one of the two ways –
- Calculate the total score (also called ‘Sigma’) of both the batsman – pick the batsman with the highest score for the next game. Or…
- Calculate the average (also called ‘Mean’) number of scores per game – pick the batsman with a better average.
Let us calculate the same and see what numbers we get –
- Billy’s Sigma = 20 + 23 + 21 + 24 + 19 + 23 = 130
- Mike’s Sigma = 45 + 13 + 18 + 12 + 26 + 19 = 133
So based on the sigma, you are likely to select Mike. Let us calculate the mean or average for both the players and figure out who stands better –
- Billy = 130/6 = 21.67
- Mike = 133/6 = 22.16
So it seems from both the mean and sigma perspective, Mike deserves to be selected. But let us not conclude that yet. Remember the idea is to select a player who can score at least 20 runs, and with the information that we have now (mean and sigma), there is no way we can conclude who can score at least 20 runs. Therefore, let’s do some further investigation.
To begin with, for each match played, we will calculate the deviation from the mean. For example, we know Billy’s mean is 21.67, and in his first match, Billy scored 20 runs. Therefore deviation from mean from the 1st match is 20 – 21.67 = – 1.67. In other words, he scored 1.67 runs lesser than his average score. For the 2nd match, it was 23 – 21.67 = +1.33, meaning he scored 1.33 runs more than his average score.
Here is the diagram representing the same (for Billy) –
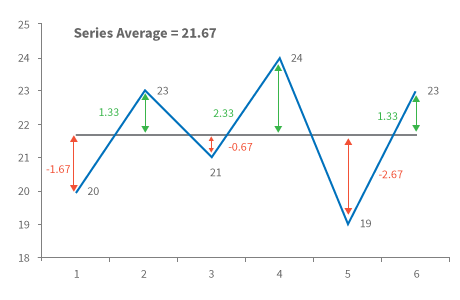
The middle black line represents the average score of Billy, and the double arrowed vertical line represents the deviation from the mean, for each of the match played. We will now go ahead and calculate another variable called ‘Variance’.
Variance is simply the ‘sum of the squares of the deviation divided by the total number of observations’. This may sound scary, but it’s not. We know the total number of observations, in this case, happens to be equivalent to the total number of matches played, hence 6.
So variance can be calculated as –
Variance = [(-1.67) ^2 + (1.33) ^2 + (-0.67) ^2 + (+2.33) ^2 + (-2.67) ^2 + (1.33) ^2] / 6
= 19.33 / 6
= 3.22
Further, we will define another variable called ‘Standard Deviation’ (SD) which is calculated as –
std deviation = √ variance
So the standard deviation for Billy is –
= SQRT (3.22)
= 1.79
Likewise, Mike’s standard deviation works out to be 11.18.
Let’s stack up all the numbers (or statistics) here –
| Statistics | Billy | Mike |
|---|---|---|
| Sigma | 130 | 133 |
| Mean | 21.6 | 22.16 |
| SD | 1.79 | 11.18 |
We know what ‘Mean’, and ‘Sigma’ signifies, but what about the SD? Standard Deviation generalizes and represents the deviation from the average.
Here is the textbook definition of SD “In statistics, the standard deviation (SD, also represented by the Greek letter sigma, σ) is a measure that is used to quantify the amount of variation or dispersion of a set of data values”.
Please don’t get confused between the two sigma’s – the total is also called sigma represented by the Greek symbol ∑ and standard deviation is also sometimes referred to as sigma represented by the Greek symbol σ.
One way to use SD is to project how many runs Billy and Mike are likely to score in the next match. To get this projected score, you need to add and subtract the SD from their average.
| Player | Lower Estimate | Upper Estimate |
|---|---|---|
| Billy | 21.6 – 1.79 = 19.81 | 21.6 + 1.79 = 23.39 |
| Mike | 22.16 – 11.18 = 10.98 | 22.16 + 11.18 = 33.34 |
These numbers suggest that in the upcoming 7th match Billy is likely to get a score anywhere in between 19.81 and 23.39 while Mike stands to score anywhere between 10.98 and 33.34. Because Mike has a wide range, it isn’t easy to figure out if he is going to score at least 20 runs. He can either score 10 or 34 or anything in between.
However, Billy seems to be more consistent. His range is smaller, which means he will neither be a big hitter nor a lousy player. He is expected to be consistent and is likely to score anywhere between 19 and 23. In other words – selecting Mike over Billy for the 7th match can be risky.
Going back to our original question, which player do you think is more likely to score at least 20 runs? By now, the answer must be clear; it has to be Billy. Billy is consistent and less risky compared to Mike.
So in principle, we assessed the riskiness of these players by using “Standard Deviation”. Hence ‘Standard Deviation’ must represent ‘Risk’. In the stock market world, we define ‘Volatility’ as the riskiness of the stock or an index. Volatility is a % number as measured by the standard deviation.
I’ve picked the definition of Volatility from Investopedia for you – “A statistical measure of the dispersion of returns for a given security or market index. Volatility can either be measured by using the standard deviation or variance between returns from that same security or market index. Commonly higher the standard deviation, higher is the risk”.
Going by the above definition, if Infosys and TCS have the volatility of 25% and 45% respectively, then clearly Infosys has less risky price movements when compared to TCS.
15.3 – Some food for thought
Before I wrap this chapter, let’s make some prediction –
Today’s Date = 15th July 2015
Nifty Spot = 8547
Nifty Volatility = 16.5%
TCS Spot = 2585
TCS Volatility = 27%
Given this information, can you predict the likely range within which Nifty and TCS will trade 1 year from now?
Of course we can, let us put the numbers to good use –
| Asset | Lower Estimate | Upper Estimate |
|---|---|---|
| Nifty | 8547 – (16.5% * 8547) = 7136 | 8547 + (16.5% * 8547) = 9957 |
| TCS | 2585 – (27% * 2585) = 1887 | 2585 + (27% * 2585) = 3282 |
So the above calculations suggest that in the next 1 year, given Nifty’s volatility, Nifty is likely to trade anywhere between 7136 and 9957 with all values in between having the varying probability of occurrence. This means to say on 15th July 2016 the probability of Nifty to be around 7500 could be 25%, while 8600 could be around 40%.
This leads us to an exciting platform –
- We estimated the range for Nifty for 1 year; similarly, can we estimate the range Nifty is likely to trade over the next few days or the range within which Nifty is likely to trade upto the series expiry?
- If we can do this, then we will be in a better position to identify options that are likely to expire worthless, meaning we could sell them today and pocket the premiums.
- We figured the range in which Nifty is likely to trade in the next 1 year as 7136 and 9957 – but how sure are we? Is there any degree of confidence while expressing this range?
- How do we calculate Volatility? I know we discussed the same earlier in the chapter, but is there an easier way? Hint – we could use MS Excel!
- We calculated Nifty’s range estimating its volatility as 16.5%, what if the volatility changes?
Over the next few chapters, we will answer all these questions and more!
Key takeaways from this chapter
- Vega measures the rate of change of premium concerning the change in volatility.
- Volatility is not just the up-down movement of markets.
- Volatility is a measure of risk.
- Volatility is estimated by the standard deviation.
- Standard Deviation is the square root of the variance.
- We can estimate the range of the stock price, given its volatility.
- Larger the range of stock, higher is its volatility aka risk.


I have asked this question to quite a few traders and the most common answer is “Volatility is the up down movement of the stock market”. If you have a similar opinion on volatility, then it is about time we fixed that: Nice play with words – I saw what you did there with ‘ fixed and volatile’ 😛
You ended this chapter as they ended the movie Inception – wanting for more as soon as possible 🙂
Saurabh, glad you noticed my little joke 🙂
Next chapter coming soon !
Its amazing. How in a simple way you can not only explain but put (fix) things in our mind so that we will never forget it.
Just one question about Infy. Today Infosys results came so naturally yesterday i.e. on 20th July volatility of infosys must have been very high compared to today. Is it right and how it has affected the premium of strikes say at ITM, OTM?
Is it not similar to the Bollinger bands theory which also i suppose works on SD of 2%. Can you explain here meaning of 2%.
Volatility has a huge impact on option premiums – we will address all your questions in the upcoming chapters. Request you to please stay tuned till then!
This chapter ended soon:(
Trying to break it into bite size chapters to make the learning easy 🙂
great work, good going. Keep it up
Thanks Suresh 🙂
Sir, in the above example on what basis you mentioned the nifty probability range as 25% & 40% in 2016?
Its based on a statistical function called ‘Cumulative Distribution Function‘ abbreviated as CDF. I will touch upon this topic soon.