16.1 – Calculating Volatility on Excel

In the previous chapter, we introduced the concept of standard deviation and how it can be used to evaluate ‘Risk or Volatility’ of a stock. Before we move any further on this topic I would like to discuss how one can calculate volatility. Volatility data is not easily available, hence its always good to know how to calculate the same yourself.

Of course in the previous chapter we looked into this calculation (recall the Billy & Mike example), we outlined the steps as follows –

1. Calculate the average
2. Calculate the deviation – Subtract the average from the actual observation
3. Square and add up all deviations – this is called variance
4. Calculate the square root of variance – this is called standard deviation

The purpose of doing this in the previous chapter was to show you the mechanics behind the standard deviation calculation. In my opinion it is important to know what really goes beyond a formula, it only enhances your insights. In this chapter however, we will figure out an easier way to calculate standard deviation or the volatility of a given stock using MS Excel. MS Excel uses the exact same steps we outlined above, just that it happens at a click of a button.

I’ll give you the border steps involved first and then elaborate on each step –

1. Download the historical data of closing prices
2. Calculate the daily returns
3. Use the STDEV function

So let us get to work straight away.

Step 1 – Download the historical closing prices

You can do this from any data source that you have. Some of the free and reliable data sources are NSE India website and Yahoo Finance.

I will take the data from NSE India for now. At this point I must tell you that NSE’s website is quite resourceful, and in terms of information provided, I guess NSE’s website is one of the best stock exchange websites in the world.

Anyway, in this chapter let us calculate Wipro’s volatility. To download the historical closing prices, visit – http://www.nseindia.com/products/content/equities/equities/equities.htm and click on historical data and select the search option.

Here is a snapshot where I have highlighted the search option –

Once you hit search, a set of fields open up, filling them up is quite self explanatory – just fill in the required details and hit ‘Get Data’. Do make sure you get the data for the last 1 year. The dates that I have selected here is from 22^nd July 2014 to 21^st July 2015.

Once you hit ‘get data’, NSE’s website will query your request and fetch you the required data. At this point you should see the following screen –

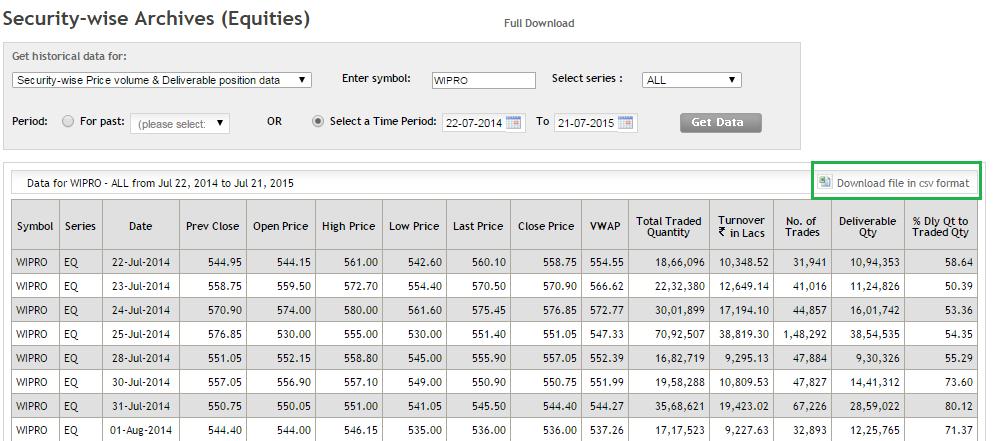
Once you get this, click on ‘Download file in CSV format’ (highlighted in the green box), and that’s it.

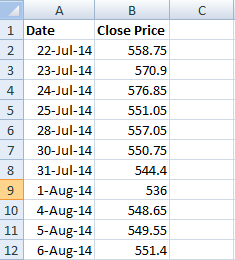
You now have the required data on Excel. Of course along with the closing prices, you have tons of other information as well. I usually like to delete all the other unwanted data and stick to just the date and closing price. This makes the sheet look clutter free and crisp.

Here is a snapshot of how my excel sheet looks at this stage –

Do note, I have deleted all the unnecessary information. I have retained just the date and closing prices.

Step 2 – Calculate Daily Returns

We know that the daily returns can be calculated as –

Return = (Ending Price / Beginning Price) – 1

However for all practical purposes and ease of calculation, this equation can be approximated to:

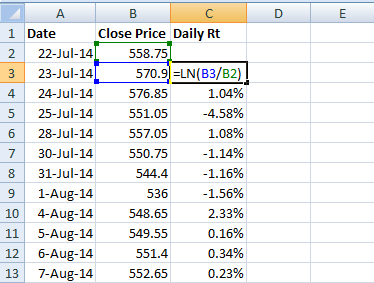
Return = LN (Ending Price / Beginning Price), where LN denotes Logarithm to Base ‘e’, note this is also called ‘Log Returns’.

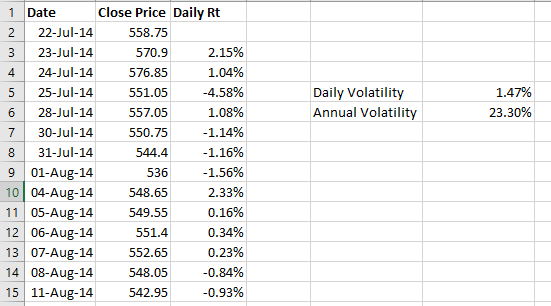
Here is a snap shot showing you how I’ve calculated the daily log returns of WIPRO –

I have used the Excel function ‘LN’ to calculate the long returns.

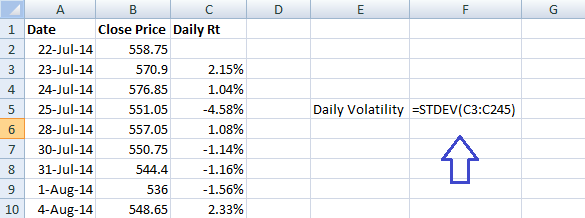
Step 3 – Use the STDEV Function

Once the daily returns are calculated, you can use an excel function called ‘STDEV’ to calculate the standard deviation of daily returns, which if you realize is the daily Volatility of WIPRO.

Note – In order to use the STDEV function all you need to do is this –

1. Take the cursor an empty cell
2. Press ‘=’
3. Follow the = sign by the function syntax i.e STDEV and open a bracket, hence the empty cell would look like =STEDEV(
4. After the open bracket, select all the daily return data points and close the bracket
5. Press enter

Here is the snapshot which shows the same –

Once this is done, Excel will instantly calculate the daily standard deviation aka volatility of WIPRO for you. I get the answer as 0.0147 which when converted to a percentage reads as 1.47%.

This means the daily volatility of WIPRO is 1.47% !

The value we have calculated is WIPRO’s daily volatility, but what about its annual volatility?

Now here is a very important convention you will have to remember – in order to convert the daily volatility to annual volatility just multiply the daily volatility number with the square root of time.

Likewise to convert the annual volatility to daily volatility, divide the annual volatility by square root of time.

So in this case we have calculated the daily volatility, and we now need WIPRO’s annual volatility. We will calculate the same here –

• Daily Volatility = 1.47%
• Time = 252
• Annual Volatility = 1.47% * SQRT (252)
• = 23.33%

In fact I have calculated the same on excel, have a look at the image below –

So with this, we know WIPRO’s daily volatility is 1.47% and its annual volatility is about 23%.

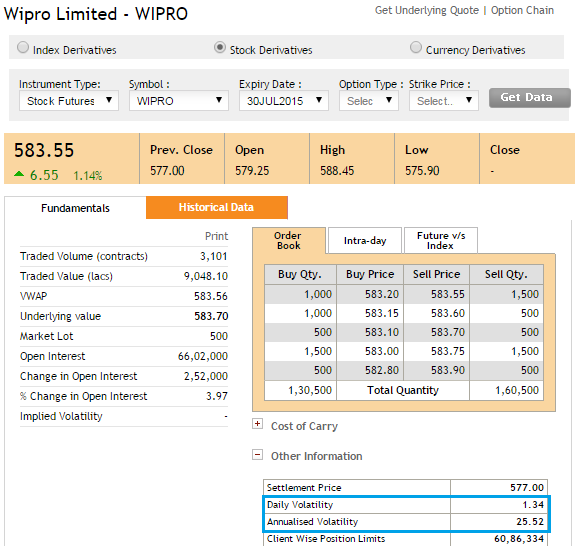
Lets double-check these numbers with what the NSE has published on their website. NSE publishes these numbers only for F&O stocks and not other stocks. Here is the snapshot of the same –

Our calculation is pretty much close to what NSE has calculated – as per NSE’s calculation Wipro’s daily volatility is about 1.34% and Annualized Volatility is about 25.5%.

So why is there a slight difference between our calculation and NSE’s? – One possible reason could be that we are using spot price while NSE is using Futures price. However, I really don’t want to get into investigating why this slight difference exists. The agenda here is to know how to calculate the volatility of the security given its daily returns.

Before we wrap up this chapter, let us just do one more calculation. Assume we directly get the annual volatility of WIPRO as 25.5%, how do we figure out its daily volatility?

Like I mentioned earlier, to convert annual volatility to daily volatility you simply have to divide the annual volatility by the square root of time, hence in this particular case –

= 25.5% / SQRT (252)

= 1.60%

So far we have understood what volatility is and how to calculate the same. In the next chapter, we will understand the practical application of volatility.

Do remember we are still in the process of understanding volatility; however the final objective is to understand the options greek Vega and that really means. So please do not lose sight of our end objective.

Please click here to download the excel sheet.

---

Key takeaways from this chapter

1. Standard Deviation represents volatility, which in turn represents risk
2. We can use NSE website to get the daily closing prices of securities
3. Daily return can be calculated as log returns
4. Log function in excel is LN
5. Daily return formula = LN (Today’s Value / Yesterday’s Value) expressed as a percentage
6. Excel function to calculate volatility is STDEV
7. Standard Deviation of daily return is equivalent of daily volatility
8. To convert daily volatility to annual volatility multiply the daily volatility by the square root of time
9. Likewise to convert annual volatility to daily volatility, divide the annual volatility by the square root of time