13.1 – The Curvature

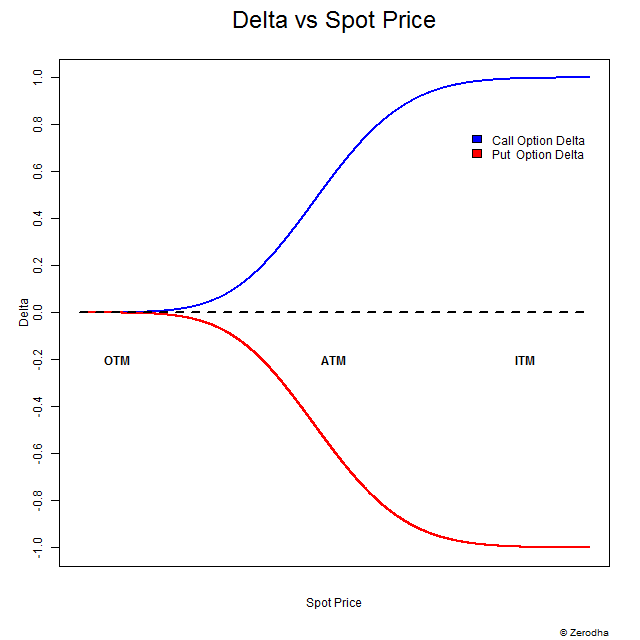
We now know for a fact that the Delta of an option is a variable, as it constantly changes its value relative to the change in the underlying. Let me repost the graph of the delta’s movement here –

If you look at the blue line representing the delta of a call option, it is quite clear that it traverses between 0 and 1 or maybe from 1 to 0 as the situation would demand. Similar observations can be made on the red line representing the put option’s delta (except the value changes between 0 to -1). This graph reemphasizes what we already know, i.e. the delta is a variable, and it changes all the time. Given this, the question that one needs to answer is –

1. I know the delta changes, but why should I care about it?
2. If the change in delta really matters, how do I estimate the likely change in the delta?

We will talk about the 2^nd question first as I’m reasonably certain the answer to the first question will reveal itself as we progress through this chapter.

As introduced in the previous chapter, ‘The Gamma’ (2^nd order derivative of premium) also referred to as the curvature of the option gives the rate at which the option’s delta changes as the underlying changes. The gamma is usually expressed in deltas gained or lost per one-point change in the underlying – with the delta increasing by the amount of the gamma when the underlying rises and falls by the amount of the gamma when the underlying falls.

For example consider this –

• Nifty Spot = 8326
• Strike = 8400
• Option type = CE
• Moneyness of Option = Slightly OTM
• Premium = Rs.26/-
• Delta = 0.3
• Gamma = 0.0025
• Change in Spot = 70 points
• New Spot price = 8326 + 70 = 8396
• New Premium =??
• New Delta =??
• New moneyness =??

Let’s figure this out –

• Change in Premium = Delta * change in spot  i.e  0.3 * 70 = 21
• New premium = 21 + 26 = 47
• Rate of change of delta = 0.0025 units for every 1 point change in underlying
• Change in delta = Gamma * Change in underlying  i.e  0.0025*70 = 0.175
• New Delta = Old Delta + Change in Delta  i.e  0.3 + 0.175 = 0.475
• New Moneyness = ATM

When Nifty moves from 8326 to 8396, the 8400 CE premium changed from Rs.26 to Rs.47, and along with this the Delta changed from 0.3 to 0.475.

Notice with the change of 70 points, the option transitions from slightly OTM to ATM option. Which means the option’s delta has to change from 0.3 to somewhere close to 0.5. This is exactly what’s happening here.

Further, let us assume Nifty moves up another 70 points from 8396; let us see what happens with the 8400 CE option –

• Old spot = 8396
• New spot value = 8396 + 70 = 8466
• Old Premium = 47
• Old Delta = 0.475
• Change in Premium = 0.475 * 70 = 33.25
• New Premium = 47 + 33.25 = 80.25
• New moneyness = ITM (hence delta should be higher than 0.5)
• Change in delta =0.0025 * 70 = 0.175
• New Delta = 0.475 + 0.175 = 0.65

Let’s take this forward a little further, now assume Nifty falls by 50 points, let us see what happens with the 8400 CE option –

• Old spot = 8466
• New spot value = 8466 – 50 = 8416
• Old Premium = 80.25
• Old Delta = 0.65
• Change in Premium = 0.65 *(50) = – 32.5
• New Premium = 80.25 – 32. 5 = 47.75 
• New moneyness = slightly ITM (hence delta should be higher than 0.5)
• Change in delta = 0.0025 * (50) = – 0.125
• New Delta = 0.65 – 0.125 = 0.525

Notice how well the delta transitions and adheres to the delta value rules we discussed in the earlier chapters. Also, you may wonder why the Gamma value is kept constant in the above examples. Well, in reality, the Gamma also changes with the change in the underlying. This change in Gamma due to changes in underlying is captured by 3^rd derivative of underlying called “Speed” or “Gamma of Gamma” or “DgammaDspot”. For all practical purposes, it is not necessary to get into the discussion of Speed, unless you are mathematically inclined or you work for an Investment Bank where the trading book risk can run into several $ Millions.

Unlike the delta, the Gamma is always a positive number for both Call and Put Option. Therefore when a trader is long options (both Calls and Puts), the trader is considered ‘Long Gamma’, and when he is short options (both calls and puts) he is considered ‘Short Gamma’.

For example, consider this – The Gamma of an ATM Put option is 0.004, if the underlying moves 10 points, what do you think the new delta is?

Before you proceed, I would suggest you spend a few minutes to think about the solution for the above.

Here is the solution – Since we are talking about an ATM Put option, the Delta must be around – 0.5. Remember Put options have a –ve Delta. Gamma, as you notice, is a positive number, i.e. +0.004. The underlying moves by 10 points without specifying the direction, so let us figure out what happens in both cases.

Case 1 – Underlying moves up by 10 points

• Delta = – 0.5
• Gamma = 0.004
• Change in underlying = 10 points
• Change in Delta = Gamma * Change in underlying = 0.004 * 10 = 0.04
• New Delta = We know the Put option loses delta when underlying increases, hence – 0.5 + 0.04 = – 0.46

Case 2 – Underlying goes down by 10 points

• Delta = – 0.5
• Gamma = 0.004
• Change in underlying = – 10 points
• Change in Delta = Gamma * Change in underlying = 0.004 * – 10 = – 0.04
• New Delta = We know the Put option gains delta when underlying goes down, hence – 0.5 + (-0.04) = – 0.54

Now, here is a trick question for you – In the earlier chapters, we had discussed that the Delta of the Futures contract is always 1, so what do you think the gamma of the Futures contract is? Please leave your answers in the comment box below :).

13.2 – Estimating Risk using Gamma

I know many traders define their risk limits while trading. Here is what I mean by a risk limit – for example, the trader may have a capital of Rs.300,000/- in his trading account. Margin required for each Nifty Futures is approximately Rs.16,500/-. Do note you can use Zerodha’s SPAN calculator to figure out the margin required for any F&O contract.  So considering the margin and the M2M margin required, the trader may decide at any point he may not want to exceed holding more than 5 Nifty Futures contracts, thus defining his risk limits, this seems fair enough and works really well while trading futures.

But does the same logic work while trading options? Let’s figure out if it is the right way to think about risk while trading options.

Here is a situation –

• Number of lots traded = 10 lots (Note – 10 lots of ATM contracts with a delta of 0.5 each is equivalent to 5 Futures contract)
• Option = 8400 CE
• Spot = 8405
• Delta = 0.5
• Gamma = 0.005
• Position = Short

The trader is short 10 lots of Nifty 8400 Call Option; this means the trader is within his risk boundary. Recall the discussion we had in the Delta chapter about adding up the delta. We can essentially add up the deltas to get the overall delta of the position. Also, each delta of 1 represents 1 lot of the underlying. So we will keep this in perspective, and we can figure out the overall position’s delta.

• Delta = 0.5
• Number of lots = 10
• Position Delta = 10 * 0.5 = 5

So from the overall delta perspective, the trader is within his risk boundary of trading not more than 5 Futures lots. Also, do note since the trader is short options, he is essentially short gamma.

The position’s delta of 5 indicates that the trader’s position will move 5 points for every 1 point movement in the underlying.

Now, assume Nifty moves 70 points against him, and the trader continues to hold his position, hoping for a recovery. The trader is obviously under the impression that he is holding 10 lots of options which is within his risk appetite…

Let’s do some forensics to figure out behind the scenes changes –

• Delta = 0.5
• Gamma = 0.005
• Change in underlying = 70 points
• Change in Delta = Gamma * change in underlying = 0.005 * 70 = 0.35
• New Delta = 0.5 + 0.35 = 0.85
• New Position Delta = 0.85*10 = 8.5

Do you see the problem here? Although the trader has defined his risk limit of 5 lots, thanks to a high Gamma value, he has overshot his risk limit and now holds positions equivalent to 8.5 lots, way beyond his perceived risk limit. An inexperienced trader can be caught unaware of this and still be under the impression that he is well under his risk radar. But in reality, his risk exposure is getting higher.

Now since the delta is 8.5, his overall position is expected to move 8.5 points for every 1 point change in the underlying. For a moment, assume the trader is long on the call option instead of being short – obviously, he would enjoy the situation here as the market is moving in his favour. Besides the favourable movement in the market, his positions are getting ‘Longer’ since the ‘long gamma’ tends to add up the deltas. Therefore the delta tends to get bigger, which means the rate of change on premium concerning the change in underlying is faster.

Suggest you read that again in small bits if you found it confusing.

But since the trader is short, he is essentially short gamma…this means when the position moves against him (as in the market moves up while he is short) the deltas add up (thanks to gamma) and therefore at every stage of market increase, the delta and gamma gang up against the short option trader, making his position riskier way beyond what the plain eyes can see. Perhaps this is the reason why they say – shorting options carry a huge amount of risk. In fact, you can be more precise and say “shorting options carry the risk of being short gamma”.

Note – By no means I’m suggesting that you should not short options. In fact, a successful trader employs both short and long positions as the situation demands. I’m only suggesting that when you short options, you need to be aware of the Greeks and what they can do to your positions.

Also, I’d strongly suggest you avoid shorting option contracts which has a large Gamma.

This leads us to another interesting topic – what is considered as ‘large gamma’.

13.3 – Gamma movement

Earlier in the chapter, we briefly discussed that the Gamma changes concerning the change in the underlying. This change in Gamma is captured by the 3^rd order derivative called ‘Speed’. I won’t get into discussing ‘Speed’ for reasons stated earlier. However, we need to know the behaviour of Gamma movement so that we can avoid initiating trades with high Gamma.  Of course, there are other advantages of knowing the behaviour of Gamma, and we will talk about this at a later stage in this module. But for now, we will look into how the Gamma behaves concerning changes in the underlying.

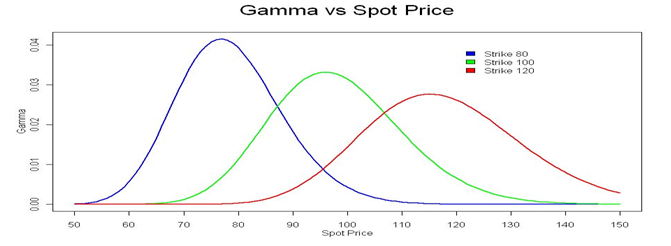
Have a look at the chart below,

The chart above has 3 different CE strike prices – 80, 100, and 120 and their respective Gamma movement. For example, the blue line represents the Gamma of the 80 CE strike price. I would suggest you look at each graph individually to avoid confusion. In fact, for the sake of simplicity, I will only talk about the 80 CE strike option, represented by the blue line.

Let us assume the spot price is at 80, thus making the 80 strike ATM. Keeping this in perspective we can observe the following from the above chart –

1. Since the strike under consideration is 80 CE, the option attains ATM status when the spot price equals 80
2. Strike values below 80 (65, 70, 75 etc) are ITM and values above 80 (85, 90, 95 etx) are OTM options.
3. Notice the gamma value is low for OTM Options (80 and above). This explains why the premium for OTM options doesn’t change much in terms of absolute point terms; however, in % terms, the change is bigger. For example – the premium of an OTM option can change from Rs.2 to Rs.2.5, while the absolute change in is just 50 paisa, the % change is 25%.
4. The gamma peaks when the option hits ATM status. This implies that the rate of change of delta is highest when the option is ATM. In other words, ATM options are most sensitive to the changes in the underlying.
   1. Also, since ATM options have the highest Gamma – avoid shorting ATM options.
5. The gamma value is also low for ITM options (80 and below). Hence for a certain change in the underlying, the rate of change of delta for an ITM option is much lesser compared to ATM option. However, do remember the ITM option inherently has a high delta. So while ITM delta reacts slowly to the change in underlying (due to low gamma) the change in premium is big (due to high base value of delta).
6. You can observe similar Gamma behaviour for other strikes, i.e. 100, and 120. In fact, the reason to show different strikes is to showcase the fact that the gamma behaves in the same way for all options strikes

Just in case you found the above discussion bit overwhelming, here are 3 simple points that you can take home –

• Delta changes rapidly for ATM option.
• Delta changes slowly for OTM and ITM options.
• Never short ATM or ITM option with a hope that they will expire worthless upon expiry
• OTM options are great candidates for short trades assuming you intend to hold these short trades upto expiry wherein you expect the option to expire worthlessly

13.4 – Quick note on Greek interactions

One of the keys to successful options trading is to understand how the individual option Greeks behave under various circumstances. Now besides understanding the individual Greek behaviour, one also needs to understand how these individual option Greeks react with each other.

So far, we have considered only the premium change concerning the changes in the spot price. We have not yet discussed time and volatility. Think about the markets and the real-time changes that happen. Everything changes – time, volatility, and the underlying price. So an options trader should be in a position to understand these changes and its overall impact on the option premium.

You will fully appreciate this only when you understand the cross interactions of the option Greeks. Typical Greek cross interactions would be – gamma versus time, gamma versus volatility, volatility vs time, time vs delta etc.

Finally, all your understanding of the Greeks boils down to a few critical decision making factors such as –

1. For the given market circumstances, which is the best strike to trade?
2. What is your expectation of the premium of that particular strike – would it increase or decrease? Hence would you be a buyer or a seller in that option?
3. If you plan to buy an option – is there a realistic chance for the premium to increase?
4. If you plan to short an option – is it really safe to do so? Are you able to see risk beyond what the naked eyes can spot?

The answers to all these questions will evolve once you fully understand individual Greeks and their cross interactions.

Given this, here is how this module will develop going further –

1. So far, we have understood Delta and Gamma.
2. Over the next few chapters, we will understand Theta and Vega.
3. When we introduce Vega (change in premium concerning the change in volatility) – we will digress slightly to understand volatility based stoploss
4. Introduce Greek cross interactions – Gamma vs time, Gamma vs spot, Theta vs Vega, Vega vs Spot etc
5. Overview of Black and Scholes option pricing formula
6. Option calculator

So as you see, we have miles to walk before we sleep :-).

---

Key takeaways from this chapter

1. Gamma measures the rate of change of delta.
2. Gamma is always a positive number for both Calls and Puts.
3. Large Gamma can translate to large gamma risk (directional risk)
4. When you buy options (Calls or Puts) you are long Gamma.
5. When you short options (Calls or Puts) you are short Gamma
6. Avoid shorting options which have a large gamma.
7. Delta changes rapidly for ATM option.
8. Delta changes slowly for OTM and ITM options.

 

Special thanks to our good friend Prakash Lekkala for providing the Greek graphs in this and other chapters.