19.1 – Point to Point return 

The previous chapter gave us a perspective of how returns are calculated given the time frame under consideration. So, now if I were to provide you with the following data point – 

Fund – Aditya Birla Frontline Equity

Starting date – 2nd January 2013

Starting investment value – Rs.1,00,000/-

Starting NAV – 100.83

Ending date – 2nd January 2015

Ending NAV – 161.83 

And asked to find out the returns, you’d probably do it with ease. Let us do the math – 

Number of units = 1,00,000/ 100.83

= 991.7683

The ending value of investment  = 991.7683 * 161.83

= Rs.1,60,497.9

The growth in this lumpsum investment over two years can be calculated by applying the  CAGR formula – 

= [160497.9/100000]^(1/2) – 1

=26.69%. 

Which as would recognize is a phenomenal growth rate. 

Now, let us say you are mighty impressed with your investment, and you start to propagate the fund. A friend walks up to you asks for the performance, and you proudly declare the 2-year growth rate is 26.69%. 

Your friend is impressed and decides to invest. 

Now, I want you to think about this for a moment. What do you think is the fundamental flaw here? 

Did you lie about your investment to your friend? – No

Did you lie or mislead your friend by letting him know the returns you’ve enjoyed? – No

Well, then what do you think is wrong here?

The growth rate of 26.69% is a massive generalization of two-year growth rate. When you mentioned this return to your friend would believe that this is the kind of performance even he is likely to enjoy. 

The 26.69% return is valid when the money is invested on 2nd January 2013 and measure its growth on 2nd January 2015. In other words, the growth rate is really only for this starting and ending points; it is right for these exact two dates.  It is a very personalized experience. 

If I were to invest and measure the returns on any other dates, then the profits will be different. 

So, whenever you measure returns or growth between two dates, the value you calculate is only valid for the two years under consideration. Hence, such a measurement of returns is also called the ‘Point to point’ return. 

To get an accurate representation of how the two-year return (growth rate) looks, you need to calculate the ‘Rolling Returns’. 

19.2 – Rolling Return  

The rolling return gives us a perspective of how the ‘n years’ return (growth) has evolved over the last ‘n years’.  Sounds confusing? I’m sure it is, so here is what we will do. 

We will take up an example and figure out the rolling return calculation. I’m sure understanding the rolling return concept becomes much easier if you know the math behind. 

By the way, many websites publish the mutual fund’s rolling return, so it is not essential to remember how to calculate the rolling returns. However, by knowing the rolling returns math, you will understand the concept of rolling return quite easily. 

So let us get started. 

I’ve got the historical NAV data of AB Frontline Equity Growth-Direct. The starting date is from 2nd January 2013, and I’ve got this till 2nd January 2020, that’s about seven years of data. 

My objective here is to find out the 2-year rolling return for this fund. To do this, I’ll have to start in 2015. 

I take the NAV on 2nd January 2015 and the NAV 2 years ago, i.e. on 2nd January 2013 and calculate the return between these two data points. Next, I move the date by one day, i.e. between 3rd January 2015 and 3rd January 2013, take the NAV for these two dates and calculate the return between these dates. I’ll again move the date by one day, i.e. 4th January 2015/2013 and calculate the return. 

So on and so forth, such that I have a time series of 2-year return. 

Let us calculate the first rolling return – 

NAV on 2nd January 2013 – 100.83

NAV on 2nd January 2015 – 161.83

Since its two years, we apply CAGR – 

[161.83/100.83]^(1/2)-1

26.69%

The 2nd rolling return in this series would be – 

NAV on 3rd January 2013 – 101.29

NAV on 3rd January 2015 – 161.45

=[161.45/101.29]^(1/2)-1

26.25%

I suppose you get the sequence. I’ve stacked up the data side by side on excel, and this is how it looks – 

The starting date is 2nd January 2015, right up to 2nd January 2020. 

As you can see, I have the latest date and NAV (shaded in blue). Next to this, I have the date and NAV for two years ago (shaded in pale yellow). I have calculated the CAGR against these two NAVs. If I do the CAGR across all the dates, I get a time series of the daily 2-year return starting from 2nd January 2015. 

Before we proceed, let us look at this statement about rolling return again – ‘Rolling return gives us a perspective of how the ‘n years’ return (growth) has evolved over the last ‘n years’. Does this sound confusing now?

I hope not ☺ 

Anyway, one minor thing to note here – look at the 2nd data point, I have NAV for 5th January 2015, but I don’t have the NAV for 5th January 2013, but instead have the NAV data for 3rd January 2013, which I’ve used. As you may have guessed, this happens due to the weekend factor. So I’d suggest you ignore this bit. 

Also, at this point, you should realize that if my objective were to calculate the 1-year rolling return, my starting point would be 2014, and if the objective is to estimate three years rolling return, then I would start from 2016. 

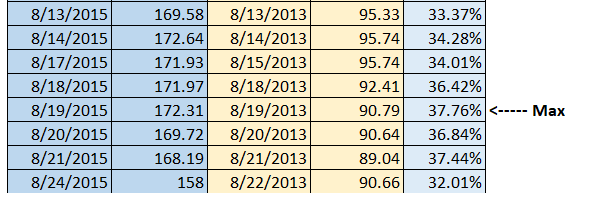
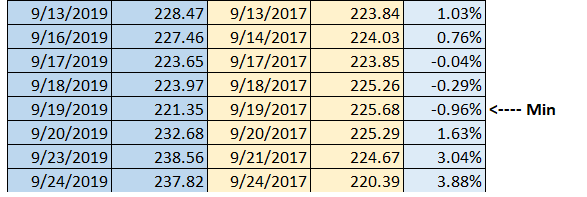
Now that we have the Rolling Return time series starting from 2015, I can do a couple of things with the data. To begin with, we can calculate the range of returns for the time series we have calculated. To estimate the range, we simply have to calculate the max and min. 

Here is the max – 

And here is the min – 

What does this mean? Well, assume two people invested in the AB Frontline Equity fund. The lucky person invested on 19th August 2013 and pulled out his investment on 19th August 2015. This person makes 37.76%. 

The unlucky fellow also invested for two years, but he/she invested on 19th September 2017 and stayed invested till 19th September 2019. Unfortunately, this person lost money! 

The point that I’m trying to make is that no two, 2-year returns are the same. The returns change depending on when you choose to invest and when you decide to pull out your investment. 

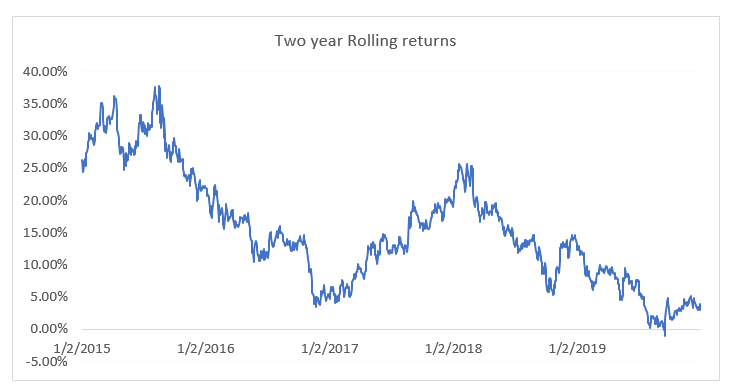
Here is a graph of the rolling 2-year return starting from 2015. 

And as you can see, the two-year returns have ranged from 37% to nearly -1.0%. If you were to invest for two years, then your return could have been anywhere within this range. 

To get a perspective of the likely 2-year return, you can take an average of the rolling returns; this is called the ‘Rolling Return Average’. 

The average is 15.35%. 

So as you can see, the rolling return gives us a lot more insights compared to a point to point return. 

So the next time you want to invest in a mutual fund, as a part of the analysis, include these two things – 

1. Identify the period you are interested in investing
2. Find out the historical rolling return min, max, and average for the period

For example, if I’m looking at investing in a large-cap equity fund for seven years, I’ll check the historical 7-year rolling return for that particular fund. By doing so, I will get a perspective of historical return range plus its average. 

In my opinion, this is much better than looking at a point to point return. By the way, I’ve used 2 years rolling return as an example. If you are looking at investing in EQ funds, then please consider at least 5 years rolling returns or higher. 

In the next chapter, let us discuss other MF metrics that matter.  

Key takeaways from this chapter

1. Point to point return gives a perspective of the return only for the two days under consideration 
2. Point to point return should not be taken as a generalization of return 
3. The rolling return gives a better perspective of the return
4. Rolling return average is a better representation of the returns one can expect