2.1 – Simple Interest

When it comes to personal finance, one of the key things to learn is the math that surrounds this topic. Once you understand the math bit, the rest is just the application of it and life becomes easy after that.

In this chapter, I’ll try and explain the most basic math involved starting from simple interest. I know this is explained across multiple chapters across multiple modules in Varsity, but for the sake of completeness let me include all of it in one single chapter.

Let us run through an imaginary transaction, my guess is that this a familiar situation for most of us.

Imagine that one of your friends needs money urgently and he approaches you for it. Being a friend, you agree to help him with the money but being a capitalist at heart, you also expect your friend to pay you ‘interest’ on the cash you lend to him. I know we don’t usually ask a friend to pay us interest, but let’s just assume he is a friend whom you’d like to help, but not at the opportunity cost of your money.

The transaction details are below –

• Amount – Rs.100,000/-
• Tenure – 5 years
• Interest (%) – 10

As you can see, your friend agrees to repay Rs.100,000/- over a 5 year period and also agrees to pay you an interest of 10%.

Given this, how much money will you make at the end of 5 years? Let’s do the math and find out the details.

Remember, the yearly interest is paid on the principal amount.

Principal = Rs.100,000/-

Interest = 10%

Yearly interest amount = 10% * 100,000

= Rs.10,000/-

Here is how the math looks –

Year	Principal Outstanding	Interest payable
01	Rs.100,000/-	Rs.10,000/-
02	Rs.100,000/-	Rs.10,000/-
03	Rs.100,000/-	Rs.10,000/-
04	Rs.100,000/-	Rs.10,000/-
05	Rs.100,000/-	Rs.10,000/-
Total Interest received		Rs.50,000/-

So as you can see, you can earn Rs.50,000/- in total interest from this payment. The amount you earn from the interest can also be calculated by applying a simple formula, which you may remember from your school days –

Amount = Principal * Time * Return  

Where the return is the interest percentage.

Amount = Rs.100,000 * 5 * 10%

= Rs.50,000/-

I’m sure you’d agree that this is quite straightforward and most of you would remember that this is simple interest.

In simple interest, the interest gets charged only on the outstanding principal.

Imagine a bank transaction, you deposit Rs.100,000/- in a bank’s Fixed Deposit scheme, which promises to pay you a simple interest of 10% year on year for 5 years. At the end of 5 years, you’ll earn Rs.50,000/- as interest income. The math is still the same.

Banks don’t pay simple interest, they pay compound interest. What do you think is the difference between simple interest and compound interest?

2.2 – Compound interest

Compound interest works differently compared to simple interest. If someone agrees to pay you compound interest, then it essentially means that the person or the entity is agreeing to pay you interest on the interest already earned.

Let’s figure this out with the same example discussed above. The transaction details are as follows –

• Amount – Rs.100,000/-
• Tenure – 5 years
• Interest (%) – 10
• Interest type – Compound Interest (compounded annually)

The math is as follows –

Year 1

At the end of 1^st year, you are entitled to receive a 10% interest on the principal outstanding and previous interest (if any). For a moment assume you are closing this at the end of the 1^st years, then you would receive the principal amount plus the interest applicable on the principal amount.

Amount = Principal + (Principal * Interest),  this can be simplified to

= Principal * (1+ interest)

Here, (1+interest) is the ‘interest’ part and the principal is obviously the principal. Applying this –

= 100,000 *(1+10%)

= 110,000

Year 2

Now assume, you want to close this in the 2^nd year instead of the first, here is how much you’d get back –

Remember, you are supposed to get paid interest on the interest earned in the first year, hence –

Principal *(1+ Interest) * (1+Interest)

The green bit is the amount receivable at the end of 1^st year, and the blue bit is the interest applicable for the 2^nd year.

We can simplify the above equation –

= Principal *(1+ Interest)^(2)

= 100,000*(1+10%)^(2)

= 121,000

Year 3

In the 3^rd year, you’d get interest on the 1^st two year’s interest as well. The math –

Principal *(1+ interest) *(1+interest) *(1+interest)

The green bit is the amount receivable at the end of 2 years, and the blue bit is the interest applicable for the 3^rd year.

We can simplify the above equation –

= Principal *(1+ Interest)^(3)

= 100,000*(1+10%)^(3)

= 133,100

We can generalize this –

P*(1+R)^(n), where –

• P = Principal
• R = Interest rate
• N = Tenure

So, if you were to have this open for the entire 5 years, you’d receive –

= 100,000*(1+10%)^(5)

=Rs.161,051/-

Contrast the difference between the 50K received in simple interest versus the Rs.61,051/- received via compound interest.

Compound interest and compounded return work magic in finance. At the end of the day, every aspect of personal finance boils down to the compounded return. For this reason, I think it is best to spend some more time trying to understand the concept of compounding of money.

2.3 – Compounded returns

The concept of compounded return is similar to compound interest. The concept of return and interest is very similar, just like the two sides of the same coin. The interest is what you pay when you borrow money in any form and the return is what you earn when you invest your money in any asset. Therefore, if you understand interest, then it is easy to understand the return.

In this section, you will learn about how the return is measured. Based on the time horizon of your investment, the return measurement differs.

You will use the absolute method to measure the return if your investment horizon is less than a year. Otherwise, if your investment horizon is more than a year, you will use CAGR or the compounded annual growth rate, to measure returns.

I guess the difference in absolute and CAGR is best understood with an example.

Assume you invested Rs.100,000/- on 1^st Jan 2019 in a financial instrument which yields you a 10% return (per year) and you withdraw this investment a year later. How much money do you make?

Quite straight forward as you can imagine –

You will make 10% of 100,000 which is Rs.10,000/-, in other words, your investment has grown by 10% on a year on year basis. This is the absolute return. This is straightforward because the time under consideration is 1 year or 365 days.

Now, what if the same investment was held for 3 years instead of 1 year, and what if instead of a simple return of 10%, the return was compounded annually at 10%? How much money would you make at the end of 3 years?

To calculate this, we simply have to apply the growth rate formula –

Amount = Principal*(1+return)^(time)

Which as you realize is the same formula used while calculating the compound interest. Applying this formula –

100,000*(1+10%)^(3)

= Rs.133,100/-

Referring to the previous section, if you were to charge compound interest, then this is the same amount of interest you receive from your friend in the 3^rd year.

Continuing on the same lines, here is another question –

If you invest Rs.100,000/- and receive Rs.133,100/- after 3 years, then what is the growth rate of your investment?

To answer this question, we just need to reorganize this formula –

Amount = Principal*(1+return)^(time)

and solve for ‘return’.

By doing so, the formula reworks itself to –

Return = [(Amount/Principal)^(1/time)] – 1

Return here is the growth rate or the CAGR.

Applying this to the problem –

CAGR = [(133100/100000)^(1/3)]-1

= 10%

2.4 – The compounding effect

Apparently, Albert Einstein once described ‘compound interest’ as the 8^th wonder of the world. I guess he could not describe it any better. To understand why you need to understand the compound interest in conjunction with time.

Compounding in the finance world refers to the ability of money to grow, given that the gains of year 1 get reinvested for year 2, gains of year 2 gets reinvested for year 3, so on and so forth.

For example, consider you invest Rs.100 which is expected to grow at 20% year on year (recall this is also called the CAGR or simply the growth rate). At the end of the first year, the money grows to Rs.120.

At the end of year 1, you have two options –

• Let Rs.20 in profits remain invested along with the original principal of Rs.100 or
• Withdraw the profits of Rs.20

You decide not to withdraw Rs.20 profit; instead, you decide to reinvest the money for the 2^nd year. At the end of the 2^nd year, Rs.120 grows at 20% to Rs.144. At the end of 3^rd year, Rs.144 grows at 20% to Rs.173. So on and so forth.

Compare this with withdrawing Rs.20 profits every year. Had you opted to withdraw Rs.20 every year then at the end of the 3^rd year the profits collected would be Rs. 60.

However, since you decided to stay invested, the profits at the end of 3 years are Rs.173/-. This is good Rs.13 or 21.7% over Rs.60 earnt because you opted to do nothing and decided to stay invested.

This is called the compounding effect.

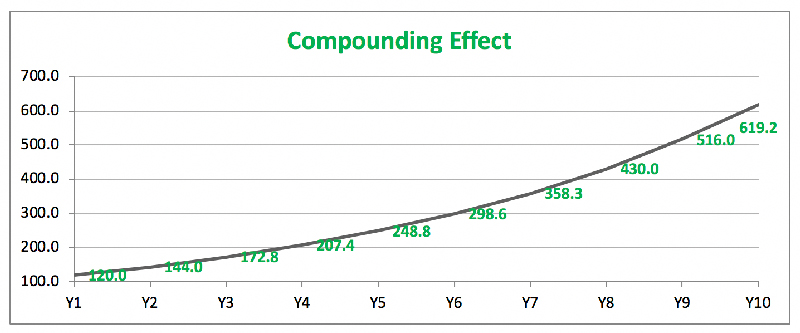
Let us take this analysis a little further, have a look at the chart below:

The chart above shows how Rs.100 invested at 20% grows over a 10-year period.

In the next chapter, we will understand the other crucial concept in personal finance – Time value of money.

Key takeaways from this chapter

• Simple interest is the interest that gets paid only on the outstanding principal
• Compound interest is paid on both interest and the principal outstanding
• Interest and return are like two sides of the same coin
• Absolute return is a measure of the growth in return when your investment is for less than a year
• Compounded annual growth rate (CAGR) is the measure of your return when your investment duration is more than a year
• Compounding works best when you give your investments enough time to grow