12.1 – Trading the equation
At this stage, we have discussed pretty much all the background information we need to know about Pair trading. We now have to patch things together and understand how all these concepts make sense while taking up a pair trade.
Let’s start with the basic equation again. I understand we have gone through this equation earlier in this module, but I want you to relook at this equation from a trader’s perspective. I want you to think about ways in which you can trade this equation. I want you to see opportunities here. This is where everything starts to culminate.
y = M*x + c
What is this equation essentially trying to tell you? Well, frankly, it depends on how your perspective of this equation. You can look at it from two different perspectives –
- As a statistician
- As a trader
Since we are dealing with two stocks here, the statistician would look at this as an equation where the stock price of a dependent stock ‘y’ is being explained with respect to an independent stock price ‘x’. This process of ‘price explanation’ generates two other variables i.e the slope (or beta) ‘M’ and the intercept ‘c’.
So in an ideal world, the stock price of y should be exactly equal to the Beta times X plus the intercept.
But we know that this is not true, there is always a variation in this equation which leads to the difference between the actual stock price of Y and the predicted stock price of Y. This difference is also termed as the ‘residual’ or the error term.
In fact, we can extend the above equation to include the residuals and with that, the equation would look like this –
y = M*x + c + ε
Where, ε represents the error or the residual of the equation. Of course, by now we are even familiar with the stationarity of the residuals which adds more sanctity to the above equation.
Fair enough, now for the interesting bit – how would a trader look at this equation? Let me repost the equation again –
y = M*x + c + ε
Let us break this equation into smaller pieces –
y = M*x , this essentially means, the price of the dependent stock ‘y’ is equal to the independent stock price ‘x’, multiplied by the slope M. Well, the slope is essentially the beta and it tells us how many stocks of x would equal the price of y.
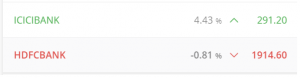
For example, here is the linear regression output of HDFC Bank (y) vs ICICI Bank (x) –
And here is the snapshot of the prices of ICICI and HDFC –
Now, this means, the price of HDFC Bank is roughly equal to the price of ICICI times the Beta. So, 1914 = 291 *7.61.
Don’t jump in to do the math, I know that does not add up ☺
But for a moment, assume if this equation were to be true, then, in other words, this essentially means 7.61 shares of ICICI equals 1 share of HDFC. This is an important conclusion.
This also means, if I were to go long on one share of HDFC and short on 7.61 shares of ICIC, then I’m essentially long and short at the same time, hence I’ve hedged away a large amount of directional risk. Don’t forget the basic premise here, we are considering these two stocks because they are co-integrated in the first place.
So here is the equation again –
y = M*x + c + ε
If this equation were to be true, then by going long and short on y and x, we are hedging away the directional risk associated with this pair.
This leaves us with the 2nd part of the equation i.e c + ε
As you know, C is the intercept. Now, at this point, I want you to recollect the ‘Error Ratio’ which we discussed in chapter 10.
Error Ratio = Standard Error of Intercept / Standard Error.
As you may recollect, we discussed the lower the error ratio, the better it is. Mathematically, this also implies that we are looking at pairs which have a low intercept.
Again this is a very crucial point for you to note, we are selecting the pairs, such that the standard error of the intercept is low.
Remember, in this equation y = M*x + c + ε we are trying to establish a trade (or hedge) every element. We are hedging y with Mx. We are trying to minimize c or the intercept because we are not trading or hedging it. Therefore, the lower it is, the better for us.
This leaves us with just the residual or the ε.
Remember, the residual is a time series. We have even validated the stationarity of this series. Now, because the residual is a stationary time series, the properties of normal distribution can be quite beautifully applied. This means, I only need to track the residuals and trigger a trade when it hits the upper or lower standard deviation!
Generally speaking, a trade is initiated when –
- Long on the pair (buy y, sell x) when the residuals hit -2 standard deviation (-2SD)
- Short on the pair (sell y, buy x) when the residuals hit +2 standard deviation (+2SD)
Like in the first method, the idea here is to initiate a trade at the 2nd standard deviation and hold the trade till the residual reverts to mean. The SL can be kept at 3SD for both the trades. More on this in the next chapter.
I know this is a short chapter, but I will conclude it here, as I don’t want to clutter your mind with other information.
It is important for you to understand this equation from a trader’s perspective and figure out what exactly you are trading. Remember, we are only trading the residuals here. We are hedging away the stock price of y with x. The intercept is kept low, and the residual is traded.
Why is the residual tradable? Because its stationary and therefore, its behavior is kind of predictable. In the next chapter, I’ll try and take up a live trade and deal with the practical aspects of pair trading.
Key takeaways from this chapter
- The pair trading equation is actually the main equation which we trade
- Every element of the equation is looked into
- We hedge the stock price of y with the stock price of x. The beta of x tells us the number stocks required to hedge 1 stock of y
- By looking into the error ratio, we are ensuring the intercept is kept low. Please remember we are not hedging the intercept, hence this needs to be kept low
- The residual is what we trade as it is stationary and follows the normal distribution quite well
- A long trade is initiated when residuals hit -2SD. Likewise, a short trade is initiated when the residuals hit +2SD
- Long on a pair requires us to go long on Y and short on X
- Short on a pair requires us to go short on Y and long on X
- When we initiate a pair trade, we expect the residual to hit the mean, so we hold until then
- The SL can be kept at 3SD for both long and short trades
Hello sir
It was quite a short chapter but very crucial i guess. Well i have a question. We can trade residual because it being a stationary time series but can we treat this data as normal distribution? I have plotted the graph of residual and it was forming skewed ND.
Thanks
Varsity student
Yes, this is a crucial chapter, hence kept it short and to the point.
As long as its stationary and has a p-value of less than 0.1 don’t bother about plotting the graphs. Just consider it stationary and look for trades.
Before reading varsity zerodha I was confuse about share market.But after reading this 10 chapters , I got lot of knowledge about stock market.I am very thankful to Nithin Kamat sir,who written varsity in so easy language.
Nithin will be happy to note this, Mahendra 🙂
Keep learning.
When i started reading the contents of Varsity in 2k16 i thought it was Nithin writing all these. But in few days i got to know it was you Karthik Rangappa 🙂 I guess many people get confused initially.
Thanks
It does not really matter, Mayank. Everything we do is as company, as a team. So credit belongs to all 🙂
You are too humble, sir. I am impressed.
Thanks
Keep learning, Mayank!
Good luck.
I took the values of residual of HDFCBANK-HDFC and in next column z-score or what you say density curve. These two stocks are highly co-integrated with p value(SIC) .0146 and 0.0054 (AIC). For shorting when Z-score>=0.975 and for long z score =<0.025.
It showed total of 4 trading opportunities during last one year and all were successful. One thing i noticed the profit gets maximised when z-score approaches 0.5 from both the sides. One more thing i noticed if one stock made gains other ended in loss.
The average net profit was 80 points. Still i haven't figure out about the stop loss. We are eagerly waiting for the next chapter.
Thanks
Varsity student
Yes, this is always true – your profits will roll only from one of the contracts, not both. However, I’ve seen instances where both the contracts make money.
True..i checked for IBULHSGFIN-HDFC. Both the contracts made money 🙂
I like this trading. We are grateful to you.
Thanks
Varsity student
Good luck, stay profitable 🙂
Brother can you please share the excel file with the above mentioned data integrated on it .
Will do that shortly, Tarun. Thanks.
I conducted ADF test on residuals of regression analysis b/w 2 stocks for case 1) stock 1 as ‘X’ and S2 as ‘Y’ case2) S1 as ‘Y’ and S2 as ‘X’. Residual of case one was non-stationary (p=0.1386) while that of case 2 was stationary (p=0.0088).
Here is the link for snapshot of the result:
http://prntscr.com/jevuqj
http://prntscr.com/jevv2u
We need your comments, sir. If this analysis is valid then we should first test for stationarity of the series before comparing error ratio, shouldn’t we?
Thanks
Varsity student
You need to select the pair based on the error ratio, Kumar. Do this first and then run the stationarity test.
Thank you!
@Kumar Mayank
which software that was? for counting probability (p-value).
i use amibroker with python to check cointegration…
can u test mail me, i want to know something more about coint…my mail is anmpatel at gmail dot com.
thanks.
Hello Akash
I use EViews to check the stationarity of a time series. Sorry, but i didn’t get you, Akash.Can you let me know what you’re asking for?
hii
Mr. Kumar
i am new at treading and have sum basic knowledge of ADF test. so can u help me out how to run ADF test in EVIEWS application please help me out of this..
Thanks in advance
It is easy to run ADF test in R package, through “urca” library. Watch this vedio
https://m.youtube.com/watch?v=mkHtP0nONJY.
@kumar mayank and Kartikji
P-value/probability/cointegration
All are same things? You use Eviews to check probability* value right?
The same thing i check in amibroker with help of python server.
I just want to check whether all r same thing with different name or not…
If same thing then its ok, otherwise i have to make some improvement with my existing system, thanks in advance.
Ya and also want to know that Eviews is free? If not how much is fees.
I’m not too familiar with either amibroker or Eviews. But yes, they are all essentially same.
Hello Akash
Two securities are co-integrated when the residuals which we get after regression analysis are stationary. The stationarity of the residuals is checked by many tests one of them is Augmented Dicky-Fuller test. The o/p of ADF test is in terms of probability. The threshold value (p-value) is 0.05 or 5%. The lower the probability value the more securities will be co-integrated.
Here is the link for EViews software: http://www.eviews.com/home.html
Thanks.
Hey Mayank, thanks for sharing the link. I’ll take a look at it as well 🙂
Welcome, sir!