6.1 – Background
Imagine a situation where you would be required to simultaneously establish a long and short position on Nifty Futures, expiring in the same series. How would you do this and more importantly why would you do this?
We will address both these questions in this chapter. To begin with let us understand how this can be done and later move ahead to understand why one would want to do this (if you are curious, arbitrage is the obvious answer).
Options as you may have realized by now, are highly versatile derivative instruments; you can use these instruments to create any kind of payoff structure including that of the futures (both long and short futures payoff).
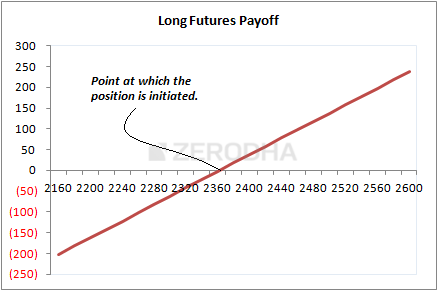
In this chapter we will understand how we can artificially replicate a long futures pay off using options. However before we proceed, you may want to just review the long Future’s ‘linear’ payoff here
Alternatively, here is a quick overview –
As you can see, the long futures position has been initiated at 2360, and at that point you neither make money nor lose money, hence the point at which you initiate the position becomes the breakeven point. You make a profit as the futures move higher than the breakeven point and you make a loss the lower the futures move below the breakeven point. The amount of profit you make for a 10 point up move is exactly the same as the amount of loss you’d make for a 10 point down move. Because of this linearity in payoff, the future is also called a linear instrument.
The idea with a Synthetic Long is to build a similar long Future’s payoff using options.
6.2 – Strategy Notes
Executing a Synthetic Long is fairly simple; all that one has to do is –
- Buy the ATM Call Option
- Sell the ATM Put Option
When you do this, you need to make sure –
- The options belong to the same underlying
- Belongs to the same expiry
Let us take an example to understand this better. Assume Nifty is at 7389, which would make 7400 the ATM strike. Synthetic Long would require us to go long on 7400 CE, the premium for this is Rs.107 and we would short the 7400 PE at 80.
The net cash outflow would be the difference between the two premiums i.e 107 – 80 = 27.
Let us consider a few market expiry scenarios –
Scenario 1 – Market expires at 7200 (below ATM)
At 7200, the 7400 CE would expire worthless, hence we would lose the premium paid i.e Rs.107/-. However the 7400 PE would have an intrinsic value, which can be calculated as follows –
Intrinsic value of Put Option = Max [Strike-Spot, 0]
= Max [7400 – 7200, 0]
=Max [200, 0]
= 200.
Clearly, since we are short on this option, we would lose money from the premium we have received. The loss would be –
80 – 200 = -120
Total payoff from the long Call and short Put position would be –
= -107 – 120
= -227
Scenario 2 – Market expires at 7400 (At ATM)
If the market expires exactly at 7400, both the options would expire worthless and hence –
- We lose the premium paid for the 7400 CE option i.e 107
- We get the retain the premium for the 7400 PE option i.e 80
- Net payoff from both the positions would be -27e 80 – 107
Do note, 27 also happens to be the net cash outflow of the strategy, which is also the difference between the two premiums
Scenario 3 – Market expires at 7427 (ATM + Difference between the two premiums)
7427 is an interesting level, this is the breakeven point for the strategy, where we neither make money nor lose money.
- 7400 CE – the option is ITM and has an intrinsic value of 27. However we have paid 107 as premium hence we experience a total loss of 80
- 7400 PE – the option would expire OTM, hence we get to retain the entire premium of 80.
- On one hand we make 80 and the other we lose 80. Hence we neither make nor lose any money, making 7427 the breakeven point for this strategy.
Scenario 4 – Market expires at 7600 (above ATM)
At 7600, the 7400 CE would have an intrinsic value of 200, we would make –
Intrinsic value – Premium
= 200 – 107
= 93
The 7400 PE would expire worthless; hence we get to retain the entire premium of Rs.80.
Total payoff from the strategy would be –
= 93 + 80
= 173
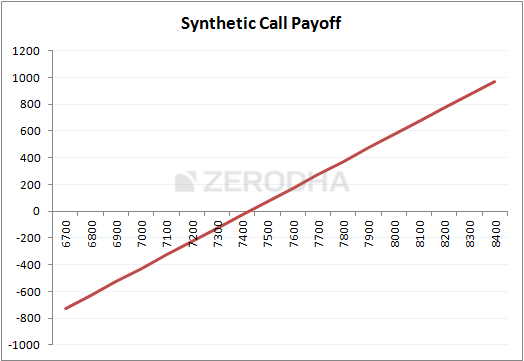
With the above 4 scenarios, we can conclude that the strategy makes money while the market moves higher and loses money while the market goes lower, similar to futures. However this still does not necessarily mean that the payoff is similar to that of futures. To establish that the synthetic long payoff behaves similar to futures, we need evaluate the payoff of the strategy with reference to the breakeven point; let’s say 200 point above and below the breakeven point. If the payoff is identical, then clearly there is linearity in the payoff, similar to futures.
So let’s figure this out.
We know the breakeven point for this is –
ATM + difference between the premiums
= 7400 + 27
= 7427
The payoff around this point should be symmetric. We will consider 7427 + 200 = 7627 and 7427-200 = 7227 for this.
At 7627 –
- The 7400 CE would have an intrinsic value of 227, hence we get to make 227 – 107 = 120
- The 7400 PE would expire worthless, hence we get to keep the entire premium of 80
- In all we experience a payoff of 120 + 80 = 200
At 7227 –
- The 7400 CE would not have any intrinsic value, hence we lose the entire premium paid i.e 107
- The 7400 PE would have an intrinsic value of 7400 – 7227 = 173, since we have received 80 as premium the net loss would be 80 – 173 = -93.
- In all we experience a payoff of -93-107 = -200
Clearly, there is payoff symmetry around the breakeven, and for this reason, the Synthetic Long mimics the payoff of the long futures instrument.
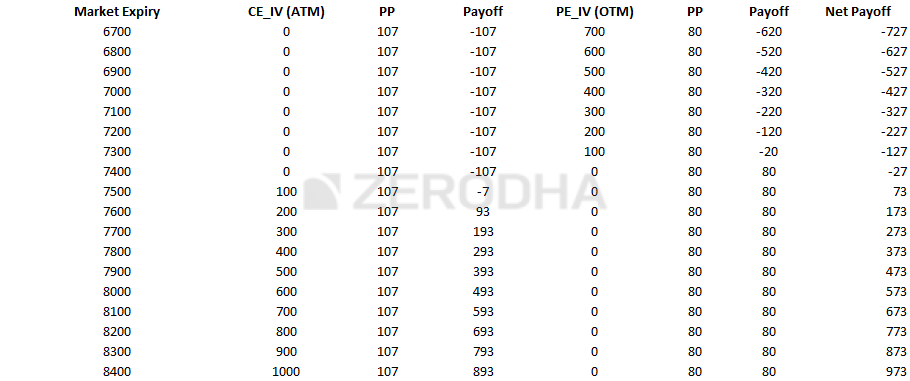
Further, here is the payoff at various expiry levels –
And when you plot the Net Payoff, we get the payoff structure which is similar to the long call futures.
Having figured out how to set up a Synthetic long, we need to figure out the typical circumstances under which setting up a synthetic long is required.
6.3 – The Fish market Arbitrage
I’ll assume that you have a basic understanding on Arbitrage. In easy words, arbitrage is an opportunity to buy goods/asset in a cheaper market and sell the same in expensive markets and pocket the difference in prices. If executed well, arbitrage trades are almost risk free. Let me attempt to give you a simple example of an arbitrage opportunity.
Assume you live by a coastal city with abundant supply of fresh sea fish, hence the rate at which fish is sold in your city is very low, let’s say Rs.100 per Kg. The neighboring city which is 125 kms away has a huge demand for the same fresh sea fish. However, in this neighboring city the same fish is sold at Rs.150 per Kg.
Given this if you can manage to buy the fish from your city at Rs.100 and manage to sell the same in the neighboring city at Rs.150, then in process you clearly get to pocket the price differential i.e Rs.50. Maybe you will have to account for transportation and other logistics, and instead of Rs.50, you get to keep Rs.30/- per Kg. This is still a beautiful deal and this is a typical arbitrage in the fish market!
It looks perfect, think about it – if you can do this everyday i.e buy fish from your city at Rs.100 and sell in the neighboring city at Rs.150, adjust Rs.20 towards expenses then Rs.30 per KG is guaranteed risk free profit.
This is indeed risk free, provides nothing changes. But if things change, so will your profitability, let me list few things that could change –
- No Fish (opportunity risk) – Assume one day you go to the market to buy fish at Rs.100, and you realize there is no fish in the market. Then you have no opportunity to make Rs.30/-.
- No Buyers (liquidity risk) – You buy the fish at Rs.100 and go to the neighboring town to sell the same at Rs.150, but you realize that there are no buyers. You are left holding a bag full of dead fish, literally worthless!
- Bad bargaining (execution risk) – The entire arbitrage opportunity hinges upon the fact that you can ‘always’ bargain to buy at Rs.100 and sell at Rs.150. What if on a bad day you happen to buy at 110 and sell at 140? You still have to pay 20 for transport, this means instead of the regular 30 Rupees profit you get to make only 10 Rupees, and if this continues, then the arbitrage opportunity would become less attractive and you may not want to do this at all.
- Transport becomes expensive (cost of transaction) – This is another crucial factor for the profitability of the arbitrage trade. Imagine if the cost of transportation increases from Rs.20 to Rs.30? Clearly the arbitrage opportunity starts looking less attractive as the cost of execution goes higher and higher. Cost of transaction is a critical factor that makes or breaks an arbitrage opportunity
- Competition kicks in (who can drop lower?) – Given that the world is inherently competitive you are likely to attract some competition who would also like to make that risk free Rs.30. Now imagine this –
- So far you are the only one doing this trade i.e buy fish at Rs.100 and sell at Rs.150
- Your friend notices you are making a risk free profit, and he now wants to copy you. You can’t really prevent his as this is a free market.
- Both of you buy at Rs.100, transport it at Rs.20, and attempt to sell it in the neighboring town
- A potential buyer walks in, sees there is a new seller, selling the same quality of fish. Who between the two of you is likely to sell the fish to the buyer?
- Clearly given the fish is of the same quality the buyer will buy it from the one selling the fish at a cheaper rate. Assume you want to acquire the client, and therefore drop the price to Rs.145/-
- Next day your friend also drops the price, and offers to sell fish at Rs.140 per KG, and therefore igniting a price war. In the whole process the price keeps dropping and the arbitrage opportunity just evaporates.
- How low can the price drop? Obviously it can drop to Rs.120 (cost of buying fish plus transport). Beyond 120, it does not makes sense to run the business
- Eventually in a perfectly competitive world, competition kicks in and arbitrage opportunity just ceases to exist. In this case, the cost of fish in neighboring town would drop to Rs.120 or a price point in that vicinity.
I hope the above discussion gave you a quick overview on arbitrage. In fact we can define any arbitrage opportunity in terms of a simple mathematical expression, for example with respect to the fish example, here is the mathematical equation –
[Cost of selling fish in town B – Cost of buying fish in town A] = 20
If there is an imbalance in the above equation, then we essentially have an arbitrage opportunity. In all types of markets – fish market, agri market, currency market, and stock market such arbitrage opportunities exist and they are all governed by simple arithmetic equations.
6.4 – The Options arbitrage
Arbitrage opportunities exist in almost every market, one needs to be a keen observer of the market to spot it and profit from it. Typically stock market based arbitrage opportunities allow you to lock in a certain profit (small but guaranteed) and carry this profit irrespective of which direction the market moves. For this reason arbitrage trades are quite a favorite with risk intolerant traders.
I would like to discuss a simple arbitrage case here, the roots of which lie in the concept of ‘Put Call Parity’. I will skip discussing the Put Call Parity theory but would instead jump to illustrate one of its applications.
However I’d suggest you watch this beautiful video from Khan Academy to understand the Put Call Parity –
So based on Put Call Parity, here is an arbitrage equation –
Long Synthetic long + Short Futures = 0
You can elaborate this to –
Long ATM Call + Short ATM Put + Short Futures = 0
The equation states that the P&L upon expiry by virtue of holding a long synthetic long and short future should be zero. Why should this position result in a zero P&L, well the answer to this is attributable to the Put Call Parity.
However, if the P&L is a non zero value, then we have an arbitrage opportunity.
Here is an example that will help you understand this well.
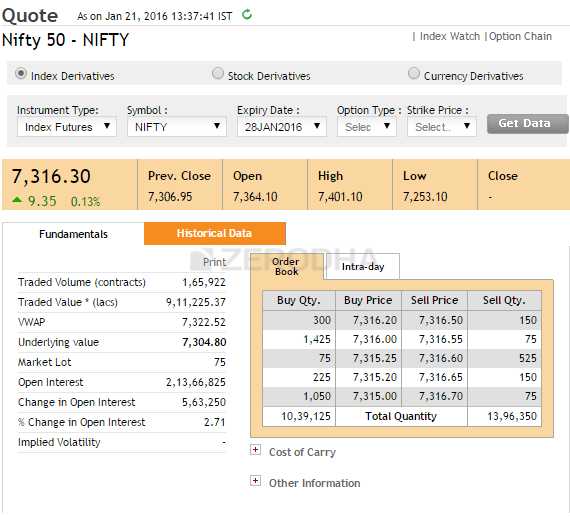
On 21st Jan, Nifty spot was at 7304, and the Nifty Futures was trading at 7316.
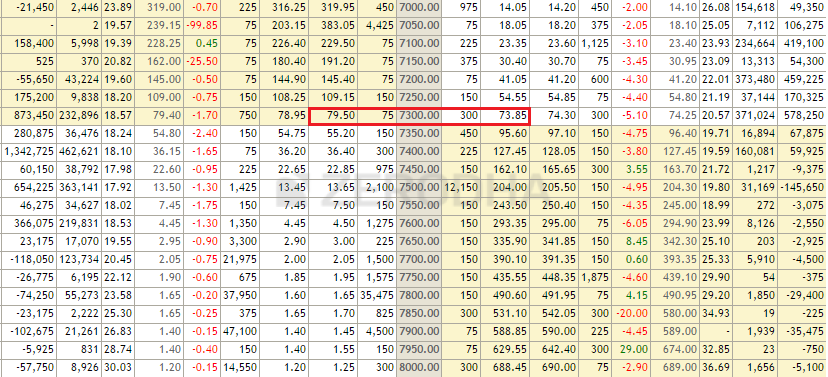
The 7300 CE and PE (ATM options) were trading at 79.5 and 73.85 respectively. Do note, all the contracts belong to the January 2016 series.
Going by the arbitrage equation stated above, if one were to execute the trade, the positions would be –
- Long 7300 CE @ 79.5
- Short 7300 PE @ 73.85
- Short Nifty futures @ 7316
Do note, the first two positions together form a long synthetic long. Now as per the arbitrage equation, upon expiry the positions should result in a zero P&L. Let’s evaluate if this holds true.
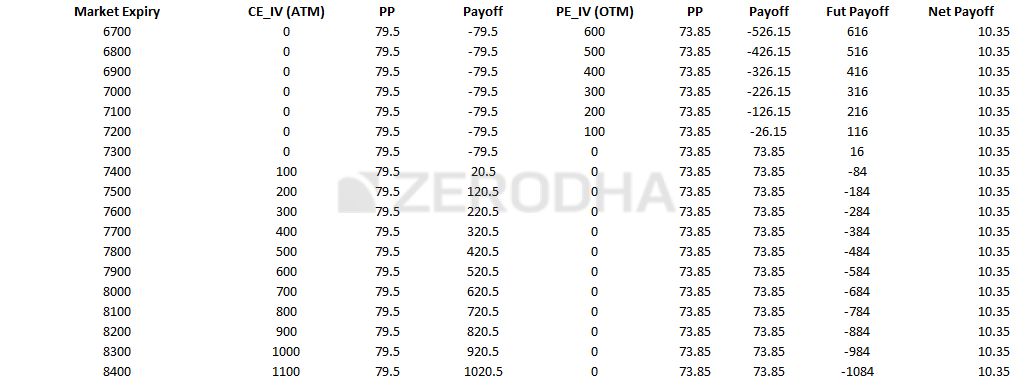
Scenario 1 – Expiry at 7200
- The 7300 CE would expire worthless, hence we lose the premium paid i.e 79.5
- The 7300 PE would have an intrinsic value of 100, but since we are short at 73.85, the net payoff would be 73.85 – 100 = -26.15
- We are short on futures at 7316, which would result in a profit of 116 points (7316 – 7200)
- Net payoff would be -79.5 – 26.15 + 116 = +10.35
Clearly, instead of a 0 payoff, we are experiencing a positive non zero P&L.
Scenario 2 – Expiry at 7300
- The 7300 CE would expire worthless, hence we lose the premium paid i.e 79.5
- The 7300 PE would expire worthless, hence we get to retain 73.85
- We are short on futures at 7316, which would result in a profit of 16 points (7316 – 7300)
- Net payoff would be -79.5 +73.85+16 = +10.35
Scenario 3 – Expiry at 7400
- The 7300 CE would have an intrinsic value of 100, and therefore the payoff would be 100 – 79.5 = 20.5
- The 7300 PE would expire worthless, hence we get to retain 73.85
- We are short on futures at 7316, which would result in loss of 84 points (7316 – 7400)
- Net payoff would be 20.5 + 73.85 – 84 = +10.35
You could test this across any expiry value (in other words the markets can move in any direction) but you are likely to pocket 10.35 points, upon expiry. I’d like to stress this again; this arbitrage lets you make 10.35, upon expiry.
Here is the payoff structure at different expiry values –
Interesting isn’t it? But what’s the catch you may ask?
Transaction charges!
One has to account for the cost of execution of this trade and figure out if it still makes sense to take up the trade. Consider this –
- Brokerage – if you are trading with a traditional broker, then you will be charged on a percentage basis which will eat away your profits. So on one hand you make 10 points, but you may end up paying 8 – 10 points as brokerage. However if you were to do this trade with a discount broker like Zerodha, your breakeven on this trade would be around 4-5 points. This should give you more reason to open your account with Zerodha ☺
- STT – Do remember the P&L is realised upon expiry; hence you would have to carry forward your positions to expiry. If you are long on an ITM option (which you will be) then upon expiry you will have to pay a hefty STT, which will further eat away your profits. Please do read this to know more.
- Other applicable taxes – Besides you also have to account for service tax, stamp duty etc
So considering these costs, the efforts to carry an arbitrage trade for 10 points may not make sense. But it certainly would, if the payoff was something better, maybe like 15 or 20 points. With 15 or 20 points you can even maneuver the STT trap by squaring off the positions just before expiry – although it will shave off a few points.
Key takeaways from this chapter
- You can use options to replicate futures payoff
- A synthetic long replicates the long futures payoff
- Simultaneously buying ATM call and selling ATM Put creates a synthetic long
- The breakeven point for the synthetic long is the ATM strike + net premium paid
- An arbitrage opportunity is created when Synthetic long + short futures yields a positive non zero P&L upon expiry
- Execute the arbitrage trade only if the P&L upon expiry makes sense after accounting for expenses.
Download Synthetic Long & Arbitrage Excel Sheet


why it is called synthetic long when on one hand there is long CE & on other hand shorting PE?
Perhaps to highlight the fact that these two positions are mimicking a short and long position.
Here all the contracts belong to the same expiry
But what will happen if I make a synthetic long using the weekly options expiring on 11 November and short the November future that expires on 25th November will the strategy work ??
Ah, I\’ve not backtested that. But it may not work as the expires differ and contracts may not work they way you\’d expect them to behave.
Is this is a total safe stretegy, if we are not considering charges like exchange, govt. and broker charges, if there is a risk what is that like market up down or others, option greeks and implied volatility.
There is nothing like a total safety strategy. Everything has risk associated with it.
is there any pre built screener where arbitrage opportunities can be found
Ah no, most of these screeners would be individuals and institutions. They\’d not like to share it 🙂
Q1- is there a way to find options arbitrage opportunities as there are many stocks and its very rare that there\’s an arbitrage opportunity in a near month contract and same happens with indexes and further we go on contracts they become illiquid.
Q2- An options arbitrage if implemented, though they are risk less strategies but what if an option goes Depp ITM or OTM and no buyers or sellers are there, what will happen in this case
Q1 – You will have to scan markets with some sort of screener. But most opportunities lie within the top 100 stocks.
Q2 – Thats the liquidity risk, which is valid with this strategy.
Hi Karthik,
I really like the way you explain the concepts and strategies on options. Thanks a lot for educating us who are new to derivative market.
I have one observation regarding iron condor strategy. The reward to risk ratio is <1 always as buy positions which are 2 strikes away would take up most of the premium received. The calculations in the chapter like RRR are lucrative but when I try for NIFTY options it is not.
Thanks, Vamsi. The P&L depends not just on strikes, but also on the premiums prevailing in the market at the time of setting up the trade.
Hi Karthik, What if the market moves opposite to our veiw? Is there any hedge possible for synthetic future strategy? Please let me know
You can always set up a hedge with normal futures.
Example
Current Nifty spot = 17806
Price of 17800 call option = 263.4
Price of 17800 put option = 145.05
(Synthetic) futures = 17800 + 263.4 – 145.05 = 17918.35.
On the same situation 17700 can be synthetic future also. So to calculate the value of synthetic future of 17700 we need to add the difference of premium of call and put to 17700 or 17800 ie ATM.
ON a simple word how to calculate 17700 synthetic future based on the above formula.
To go long (synth futures), you need to buy a call and sell a put. So the premium you receive for the selling the put minus the premium you pay for the call should give you an indicative value of the synthetic call.
How to calculate a value of synthetic future other than ATM.
Means the difference between call and put premium suppose to add with that strike or add mandatory ATM strike price.
Sorry, I\’m unable to understand your query fully. Can you elaborate please?
Can we create synthetic future in all liquid strick price other than ATM STRICK.
Can we hedge monthly synthetic future (not ATM) with cash market(ie buy/sell equivalent preperation cash stock of index) to replicate cash and carry arbitrage.
Sure, as long as there is liquidity and there is no execution risk, price slippages etc.
In sensibull i put this order and payout give positive results, but my concern about margins because the order which i want to execute is not possible at same time. Then the margine require more for this strategy. Can i buy CE and Sell pe atarket price and short future on limit price as a forever order for margin benefit?
Yes, if you use spreads, the margin requirement reduces.
Hello, just want to know that let if i buy ATM call and sell ATM put at morning session where the difference between the premium is suppose 30 point. and short a future in afternoon when the future price and spot price difference is more than 50 point to make profit of 20 point in expiry. so still the strategy work?
YOu can actually upload these positions on Sensibull and see how it plays out.
Hi Karthik,
I am looking to create a synthetic long position in Nifty with hedge.
What will be the margin requirement for the following option strategies in extreme cases, for instance if Nifty hits a lower circuit?
(a) synthetic long future in Nifty (Buy CE + Sell PE)
(b) synthetic long future in Nifty (Buy CE + Sell PE) with PE buying for hedge.
Secondly, is margin requirement fulfilled from equity collateral funds available in the above case or
additional funds need to be added in the account?
Ah, the margin required keeps varying. You can now use the margin calculator on Kite itself to figure this. Yes, margin can be fullfilled from collateral as long as the collateral is in the approved list of collateral.
Okay karthik, Found out. Thanks for your suggessions.
Sure, happy learning!
Am using sensibull only, but since the option geeks are dynamic the projection keeps on changing during trading hours, hence it would be helpful If you can give an example.
Thats right, all greeks are dynamic in nature and they keep changing. YOu need to figure the greeks that works for your trade setup at the time of initiating the trade itself.
Sorry am novice in this. I found this arbitrage box spread strategy but the profit is less than the transaction cost, so I have applied the same concept in current week plus next week synthetic future, The only thing am not able to identify is that which one is cheaper and which one is expensive. If you can give an example it will be really helpful.
Any sort of arbitrage opportunity has lesser profits, Yoga. The more number of legs means higher expense, no other way around 🙂
Hi Karthik
If i wanted to trade suppose expiries of current week and next week synthetic futures of same strike, how to identify which one is expensive.
You can always use an options calculator to figure what is the fair value of the option. I\’d suggest you use Sensibull for this.
Can this page be updated? There was a big change in STT.
Checking on this.
hi, i wanted to execute synthetic and underlying equity basket on the expiry day as an hedge.. any good software to do that ?
You can easily do that on Kite itself, right?
Thanks for the information!!
Sure, happy trading and learning 🙂
But sir, an earlier comment on August 31st, 2021 by W choudhary: he said that he suffered losses. You said the reason is because he held the positions till his expiry. Is it due to the margins required in the last few days?
Farmaan, in most cases full potential of arbitrage trades is realise upon expiry, but you can choose to close it before if you feel you\’ve raked in enough profit before expiry.
Suppose now the nifty currently is at 19500, nifty fut sep is at 19600. To make use of this opportunity(19600-19500=100), shall I
Buy 1 19500 SEP CE,
Sell 1 19500 SEP PE,
Sell 1 NIFTY SEP FUT?
The spot and futures price will converge as the time to expiry nears. But should I square off just before the expiry or should I keep it till expiry and allow the exchanges to square off? Will there be any losses then?
But do pay attention to the costs involved. In most such cases, holding till expiry is when you will reap the complete benefit of the strategy.
Thanks for prompt reply.
Physical settlement is only for stock options. Nifty Index options are still cash settled. Right?
Yup, Parvesh. Thats right.
Dear Sir, if we go long via synthetic future with deep ITM strike (say 14000 strike for CE and PE) and go short via synthetic future with deep OTM strike ((say 22000 strike for CE and PE)) for same expiry, will there be any risk if we hold the trade till expiry?
So all futures and ITM options will be settled physically, except if the positions offset each other. As far as the directional risk is concerned, it is minimized as long as the overall position is directionally neutral.
So far,, so good, thank you for taking the time to share your knowledge and explain in so much detail. Appreciated!
Wondering… how would a Reverse Arbitrage (if that\’s what it\’s called) trade be initiated? Herein, the Futures price is less than the spot price by, say, 10 points.
Thanks, Bharath. The reverse is also called an arbitrage 🙂
In such a case, you\’d buy futures and sell the spot.
Sir one doubt…nifty spot price 7304 suppose nifty future price 7409
What a strike price I can choose??
Nifty spot 7300 Atm
Or
Nifty future 7400 Atm
Maybe 7400.
Sir, can it be used for weekly expiry ?
And is it used on same expiry of future and options .
Yes, you can experiment with weekly expiries.
Sir , is this short arbitrage strategy for declined market or can it be applied for bullish maket?
Execution risk is there if it is not liquid. Index futures are quite liquid for execution.
Yeah, but I just wanted to highlight the risk, just in case you are thinking of stocks 🙂
Technically there is no risk right. Even if the spread is giving me 8 to 10% annually excluding the tax then it’s worth doing as it doesn’t carry any risk.
You have the execution risk, Utkarsh.
Can we do arbitrage in 2 different expiry future contracts.? For eg buy nifty current month futures contract, and sell next month futures contract of nifty.
Is this doable. If yes then it’s a good source of passive income with zero risk and better then FD returns
Technically yes, you can, as long as the spread between the two contracts is good enough for a decent profit. However, you cant really compare this to a FD return as the risk profiles don\’t really match.
Very well explained Karthik! Tks. Sounds like a good idea to profit from put-call parity disruptions that show up regularly in the market. One of my strategies would be shorting the synthetic weekly future and going long on the far month futures, when there is significant and substantial call premium as compared to the corresponding Put premium. Doing the opposite when weekly Call premiums are significantly lower than the Put premiums. Just wondering if there is a threshold difference between call and put premiums above or below when it makes more sense to execute this strategy? Tks once again!
Raman, the thereshold can be on volatility (as it anyway impacts premiums) instead of the premium itself.
Hi Mr. KR, please throw some light on the recent structure of stt on this kind of trade for equity segments
Short future, buy CE and sell PE.
what happens if CE or PE becomes ITM. what happen if we do not square off.
what happens if we do not square off futures
please reply. thank you so much
YOu now need to look at it from the perspective of physical settlement. Do check this chapter – https://zerodha.com/varsity/chapter/quick-note-on-physical-settlement-2/
Sir i have question, would this strategy work\’s on weekly expiry options.
If yes, then what i take as (future short) for this strategy in real time.
Please pinned a video or screenshorts for more clarity.
Yup, you can but I guess the opportunities for weekly will be harder to spot (and execute). For short, you still use the monthly futures.
Sir
First of all kudos to you for your brilliant teaching. And to Varsity for keeping this FREE. I don\’t think there is any material out there on the internet that is anywhere near to this.
Now coming back to arbitrage, my doubt is that since this is such a simple and risk free technique, wont there be powerful software out there being used by big institutions which would snap up these opportunities in seconds? If that\’s the case, is it prudent for small retail investors like me to spend their time in searching for these opportunities
Sachin, yes, Algos take up such opportunities. If you know programing, maybe you could give it a try as well 🙂
Hi Sir,
Why only ATM call buy & Put sell is considered as synthetic long. The result will be same for ITM & OTM strike prices right?
Regards,
Jeeson
The payoffs are a little different for OTMs (I think). I need to double-check this as well.
In a lecture series that is about learning basic strategies, this kind of bogus strategies should not be taught. There is no structure, no definition and no explanation for this strategy like the other ones and it is just a complete time waste. This is not a strategy, just a gimmick because this can only be pulled off by people with in depth knowledge of market and people with great command on technical analysis. This is not a strategy to teach but to discover when you are already a established trader.
Sure, Jimmy. Just to point, we also have other content available here to help you get the overall context and understand markets and this particular topic better.
How much capital is required for above arbitrage oppurtunity ?
and their ROI after accounting brokerage and other exp.
It depends on the contract you are trading. You can use this – https://zerodha.com/margin-calculator/SPAN/
You are just awesome @Karthik Rangappa . This entire series is best on internet when it comes to understanding options series . People are literally charging huge amount just to explain these points .
Kudos to entire zerodha team .
Thanks for the kind words, Rupesh. Happy learning!
Hi Mr. kartik, once again, below is the interesting question from maheswaran of 2019. please do clarify. thanks lot.
————-
Maheswaran R says:
May 14, 2019 at 7:18 am
I need bit clarity and let’s talk with an example
Ref. data below as per your excel
Stock: INDIANB
Spot : 227
Long Call (ATM): 220
Short PUT (ATM): 220
Long Call Debit for Long Call: 56
Debit for Short Put: 5
Net Premium: -51
Short Futures: 227
Spread: (-44)
here as per my understanding i need to execute the trade as below
1. Buy CE @ 56
2. Sell PE @ 5
3. Sell INDIANB Future @ 227
In this case if i execute the trade i will gaining profit of Rs 44 on expiry or Loss?
Reply
Karthik Rangappa says:
May 14, 2019 at 11:59 am
On the option leg, you are long and you are short on the futures leg. Technically you are supposed to make the spread. The spread is 227 – 220 = 7. Not sure how you arrived at -44. I’d suggest you use the excel sheet to see the overall payoff. Good luck!
Reply
Maheswaran R says:
May 14, 2019 at 10:30 pm
Thanks Karthik for you prompt reply,
-44 is Spread output by your excel formula only (i didn’t arrived my own)
Spread = (Short future – Strike Price) + Net Premium
Spread = (227-220)-51
Spread = -44
I confused again whether anything to be changed in excel calculation
Karthik Rangappa says:
May 15, 2019 at 6:02 am
Let me check this and get back to you again. Thanks.
The explanations are in the comments itself 🙂
Hi Karthik, did you clarify the below. thanks.. i would also like to know the doubt about query from Maheswaran. thanks.
—————-
Maheswaran R says:
May 14, 2019 at 10:30 pm
Thanks Karthik for you prompt reply,
-44 is Spread output by your excel formula only (i didn’t arrived my own)
Spread = (Short future – Strike Price) + Net Premium
Spread = (227-220)-51
Spread = -44
I confused again whether anything to be changed in excel calculation
Karthik Rangappa says:
May 15, 2019 at 6:02 am
Let me check this and get back to you again. Thanks.
Oh no, lost track and context of this 🙁
Kartik, what if I buy a delta 90 option of 12 month expiry and sell delta 10 option same expiry, that means I have a future…..and what if I keep doing it year after year (roll over) , then the return can mimic nifty at less capital requirement….is this a sound strategy?
YOur net delta will still be 80 (net long) and will have a directional bias. Besides you also need to factor in the Theta for it.
Hi Karthik, I was wondering if someone can use synthetic positions to exploit abnormal spreads between spot and futures prices?
This was inspired by a spread of ~₹150 in Bajaj Auto cash and futures levels today.
Theoretically one could build a synthetic short position (+1 ATM PE and -1 ATM CE) and then buy the futures to capture this spread, right?
Would love to have your opinion about this.
Thanks!
Of course, you can do this. Make sure there are no corporate actions around and factor in all charges.
Sir , can we buy OTM call or sell ITM PUT OR Sell future ?. For example , nifty is at 16250 and I want to buy 16350 OTM call and sell 16350 ITM PUT AND short future ITM put has sufficient liquidity more 1 lakh . I think it is more forfeitable and in excel of yours it is also showing profit.
Perhaps, it depends on the premiums.
Also looking at investment it requires approx 1 lakh for nifty future, approx 1 lakh for selling PE and approx, 25000 for buying CE. Total 2.25 lakhs max profit will be 1250. Brokerage is 120 for buying and selling and STT. Seams strategy works however beneficial to pay taxes and brokerage.
Cool, like I said back test once to see how the strategy responds across different market cycles before deploying capital.
I have done some calculation. I think Buying and selling CE and PE is helping to manage risk of nifty future. Can we say that if we sell nifty future at multiple of 25 will again result in 25 points. Please suggest what do you think.
I\’m not sure if I fully understand your query. But what you can do is backtest the data and see if the strategy has behaved the way it should, that way you will know what to expect.
Karthik, Help me, my understanding is correct or not
1.We can go long/short in options like futures by using the options (i.e synthetic long or synthetic long )
I\’ve analyzed the same in the excel sheet that you\’ve shared, please find the below data
Particular Value
Underlying Nifty
Spot Price 17670.45
Long Call (ATM) 17700
Short PUT (ATM) 17700
Long Call Debit
for Long Call 132
Debit for
Short Put 134
Net Premium 2
Short Futures 17737.95
And my spread is \”39.95\”, this suggest that I can execute this strategy and have to hold on till expiry, then my pay off would be \”39.95\” points ?
3.Can I execute the same in weekly, monthly and far month contracts in Index and also same in stocks for the high liquid stocks ?
And also, the options are weekly, monthly and futures are monthly, if I execute this strategy for weekly with the monthly futures, will
it work ?
4.is the market direct matters ? it would be the same effect if I do with the put option for short as like below
Long Put option(ATM)
short call option(ATM)
Buy futures
1) Yes, provided both CE and PE belong to the same expiry
2) Yes, but ensure both the legs belong to the same expiry
3) Hmm, no. It may not, although I\’ve never tried this
4) Yes, its the same.
I don\’t know why but I just remembered my 10th class while reading this strategy 😅
Maybe you would have learnt something similar in 10th 🙂
what kind of permissions
Exchange permissions, Shivansh.
Umm sir delta of ATM call is 0.5 and that of futures is 1 so instead of a synthetic arbitrage if I\’m bullish on the index won\’t I buy 2 ATM calls and for bearish I\’d go for 2 ATM puts what\’s the difference and pros or cons of these two 1. Going for a arbitrage 2. Buying two ATM options?
Yes, that\’s possible too Chetan. YOu can use Synthetic to get long and short in the market simultaneously and lock in a spread (if at all there is one).
I had a word with people at streak regarding this arbitrage topic they currently don\’t have it.
so, is there any other way I can trade arbitrage or create an Algo for it or how do you trade these arbitrage opportunities
You will have to create your own algo and get the necessary permission for the same from exchanges.
can arbitrage algo opportunities be set from STREAK
Depends on the input parameters for your algo. I think its best you take this up with Streak.
So that means options do carry a high liquidity risk ..?
Yes, of course.
Sir is the zerodha 20 market depth or level 3 data available for option contracts too ? It would really be efficient if available to estimate cost of transaction 🙃🙂
Noted, but there is hardly any liquidity 🙂
Sir, keeping all this strategies in one side but why are we shorting ITM calls (bear call ladder) when the the earlier modules it\’s said that avoid shorting high gamma options and ITM had the max gamma 🙃
Chetan, we are not shorting naked options here, its hedged right?
When & how should we exit from the arbitrage trading? ( in basket order we can square off all the position at a single time)… Let\’s say I took an arbitrage position In ABC Share on 3rd Feb 2022.. Shall we have to wait upto the expiry day? r can i exit all the position on 4tb feb itself?
You can exit the position whenever you think the arbitrage position no longer offers the arbitrage. No need to wait till expiry.
Hi Karthik
It’s interesting and very tangible that all the concepts of strategies have been out across taking intrinsic value as base for calculation but we already know how time value impacts the premiums. Knowing that, shouldn’t we Att done point cater and carry out breakdown of the same including the time value. I know you’ll say vega will act as per time left to determine the actual price but shouldn’t there be a metric to at least determine the same or maybe an easier way to calculate B&S formula knowing the parameters.
PS: I’ve a strong hunch you’ll redirect me to option formula calculator either way.
Ansul, B&S formula is just about entering a few input parameters and you get the breakdown. It is fairly straightforward 🙂 If you just want time value, then you just have to deduct the intrinsic value from the premium and the excess is time value. To calculate the intrinsic value, you don\’t really need B&S. Ask yourself, what is the value of this option if it were to expire right now. If the value is 0, then there is no intrinsic value, all the premium is attributable to the time value. Guess I\’ve explained this in the previous module in the Theta chapter.
Sir, What if we sell future contract of next month than selling of current month?
Saurabh, you can do that. Costs may increase.
Hello Sir, firstly I would like to thank you for explaining such a complex topic like options in such a lucid manner. My question is under what market conditions is the synthetic long strategy implemented?
Thanks for the kind words, Abhishek. I\’m glad you liked the content on Varsity. You can deploy this based on your capital and margin availability. It is more of a choice based on capital availability than market condition.
Hi..can you tell the sequence of placing this strategy and also the sequence for exit.
buy first then sell or how to do it. thanks.
Place the buying part first so that the margins for the sell leg is lower.
hello sir,
sir can arbitrage a position b/w nse and bse
graphite india trading at 602 (bse )
723(nse )
can we arbitrage this ?
Buy in BSE, sell in NSE. But the question is how will you sell in NSE?
Will I get margin benefit if I buy 1 lot of Nifty current month futures using Zerodha and sell one lot of the Nifty futures next month using Upstox?
No Sir, you wont.
Can I short stocks in far month future market and immediately but in cash market, if I don\’t have stocks in delivery?
Yes, you can. For the short futures (whichever month), you need to ensure you have stock by the delivery date.
WHAT IF OPTIONS PREMIUMS PRICE CHANGES ??
Since it\’s a spread, the spread should remain intact.
Yes sir I implemented this on August expiry and hold this spread to expiry day.
Sure, good luck. I hope the profits roll 🙂
I implemented this strategy with approx 30 points spread but on expiry day instead of profit I suffered a loss can you plz tell me how can I plan my exit in this strategy?
Did you hold this to expiry?
In arbitrage only entry is important and also very difficult to identify in indexes by naked eyes. Stocks always have arbitrage but poor execution and liquidity risk. Always look at bid-ask price instead of premium. And u cane create synthetic long and synthetic short at the same time instead of trading future. The margin would come down. It is like iron condor in a way. But p&l is fixed wherever the market goes.
Hi Karthik,
In all the scenarios, why haven\’t you considered the lot size of futures while calculating the future\’s pay off ? In the excel when market expired at 6700, isn\’t the future\’s payoff is 75*(7316-6700), where 75 is the lot size ?
Thank You
Lot sizes keep varying, Sreejith. Also the payoff is the price difference, your Profit (or loss) is always multiplied by the lot size, so they are two different things technically 🙂
Is it possible to spot this arbitrage arbitrage manually from your experience
2) what if we get negative insted of 0
For an experienced eye, yes, possible.
What if I am making a arbitrage with selling jul banknifty future and selling 35300 put and buying 35300 call (weekly option) and opstra is showing profit of 2430 when would I get this 2430 rupees whether I have to square my postion on Thursday at 3:15 or let it expire as it is on Thursday?
Yes Sahil, you need to square off the position by expiry.
Sir how to spot an arbitrage opportunity? I mean how to find out which stocks are presenting it or at what time is it arising in an index?
Thanks to the algo, spotting an arbitrage opportunity is becoming increasingly hard, Prashant. You can try things like pair trade for arbitrage, these are relatively easier to identify and set up.
Hii sir
Sir, presently ITC jun futures is trading around 205 and august futures 207, buying June and selling august is an example of arbitrage trading?
As I analyze, it does not show any loss or breakeven.
Hmm, you can. But there is no guarantee that these prices will converge by June expiry.
Dear Sir,
Should one implement a long combo (buy OTM call, sell out Put) instead of synthetic long future (buying ATM call, sell atm put). The cost reduces however there is a gap between strike prices.
It seems cheaper to implement if one does not plan to hold till expiry?
What do you suggest?
You can do that, but the payoff may differ, Hasan. Please put this in Sensibull and check the payoff.
yes. i bought CE and then sold futures.
Please do check with the support desk for this.
i am having problem with Zerodha, margin calculator and actuals are very different. Today i was going for this synthetic strategy but i was not allowed even though margin it was looking for was available
– i bought SBIN 420 CE at 16.8
– 1 sold SBIN futures at 416
Margin used for this under funds show 60000, while zerodha margin calculator says it should be 31000
now, i was planning to sell SBIN 420 CE at 22, while the margin requirement showed in the sell dialog was 23000 and i had margin of 60000 in my account even then i was not able to place the order
I hope you have bought the call before selling the futures.
Dear Sir,
Can you do a synthetic long using different strike prices?
For example
I purchase 15300 PE and sell 15350 CE for 275, 278
This essentially makes increases my breakeven to a 15353 from 15331. This would be a good thing correct??
I have seen people buying 15300 CE and selling 15000 PE. What is the purpose of such a thing?
If you want a synthetic long or short, then the strikes should be same. Only then will the pay off match that of a futures. Else, the payoff will be very different and will have its own risk-reward profile.
sir
insted of synthetic long in nifty.
is it better to go long in nifty?
Yes, synthetic is just an alternate solution.
Sir should I close the position ( all 3 legs) on click (simultaneously) or should i square off one by one
I\’d suggest you close one after the other.
Sir my above query is for expiry day
And also same happened to me today in bank nifty and premium is dropped by 100 points.
Sure, the same holds for expiry as well.
I implemented this strategy and pay off for put in excel showed 242 price when nifty is at 14708 but in live market the put premium is around 252 when nifty future is at 14708.resultant 10 point loss…..
My query is how to deal with this above situation.
The excel sheet suggests the pay off at expiry, and not during the series. Btw, there is a utility in Sensibull which kind of gives you the estimate of P&L if you were to close the position before expiry.
i got it, the sequence should be Option CE buy, Futures sell and Option PE sell
Good luck 🙂
Today i was planning to try this and was looking for margin requirement in Zerodha calculator. Zerodha margin calculator showed me that i will need 55000 for buying Nifty 14900 May CE, selling Nifty 14900PE and selling Nifty May Futures. I had 58000 in my account but still i am unable to proceed.
I bought Nifty 14900 May CE first and once the order was executed i planned to sell 14900 PE, but it is not allowing me to sell 14900 PE, showing me insufficient margin.
Did you also have the futures order pending?
Dear kartik thank you for sharing this knowledge. I want to know as in 2021 is there is any changes. What happen if i hold the positions till expiry to capture maximum profits. And can we use arbitrage(on a good opportunity for sure) to get a return of over 10%( by new margin rules).
All questions are related to arbitrage kindly please answer
There are no changes as such, Shivendra. These are conceptual notes, won\’t change in time. Yes, you can hold to expiry (in fact that\’s preferred if possible), although I\’m not sure about the returns bit 🙂
When i analyze this trade in zerodha basket, it usually shows more than 2% profit without any loss.
But i have one doubt, as you said that profit is realized on expiry so can we buy and sell ATM of weekly expiry and short nifty futures which are in months, will this work ??
Yeah, works for weekly as well, but ensure the spreads are profitable.
Hello Sir,
Reading some of these nasty comments. Please ignore them if you can.
The fact that you have put 6 years of your into writing a FREE financial literacy book for anyone and everyone is nothing next to phenomenal.
At most you gain zerodha a few more customers who having read your modules and enter the market but I see no self gain for you in this.
The stuff you are teaching is generally taught in some university level classes where you have to pay a lot of money.
Thank you for everything sir, I have learnt a lot from these modules and really hoping for You and your family\’s further success.
Thanks so much for these kind words, it made my day 🙂
Comments like these are what encourages us to put up such comments on a regular basis. Hope you continue to enjoy reading on Varsity.
Sorry, I have not used any kind words and only I expressed my unhappiness for the very severe bad comments made by V Bharathi and I was pained that so many beneficiaries who took knowledge from you for earning good less risky money have not come to support their knowledge imparter.
Thats ok Sir, don\’t worry about it, but many thanks for your support, I feel humbled.
I am very much pained by reading the unwarranted criticism of V Bharathy on Shri Karthik Rangappa vide her severe criticism on a petty issue on which Shri Rangappa shown finally what position taken by V Bharthy was wrong,. The unwarranted criticisms are there above in the remarks by so many people.
I am pained much more for none of the so many beneficiaries, of knowledge imparted by Shri Rangappa, have come in support of a revered imparter of knowledge. Though many a readers expressed in glowing terms their veneration for Rangappa none came in support of him for the severe ill comments made by V Bharathy against Rangappa and his teaching ability.
People who are taking freely the knowledge, must have some sense of responsibility also when they are getting benefited
Thanks for the kind words.
One of the great things about markets is that it teaches you to stay grounded and take every opinion with the right spirit. After all, different opinions are what makes the market 🙂
Mr Karthik
After executing arbitrage trade, what will be exit parameters. Do we need to wait until expiry or whenever profit is there we can exit from that trade. Plz, clarify my doubt.
YOu can exit whenever you think is a good opportunity to exit. No need to wait to expiry.
Does zerodha allow us to cash n carry this trade? I didn\’t see anything except Intraday or overnight buy while trying Long call, Short put & Short Future
NRML in F&O = CNC or cash n carry. Is that what you are referring to?
Why should we ATM strike price? Can\’t we use other strike prices?
You can, but that changes the dynamics of the payoff.
Not sure, need to check with the team.
hello sir,
sir if we are implementing arbitrage on weekly expiry , can we short monthly expiry future ?
It is better to stick to the same expiry that you are implementing with.
HI There,
I have been observing Put Call Parity for quite some days,
I do See it daily when the market makes a good move
I have 2 Questions?
Todays example:
CE 180
Strike 14900
PE 166
Future 14945
There is 31 point how i can encash It.
Is it possible to exit the trade before expiry?
How much will be the brokerage in zerodha?
Reply
Karthik Rangappa says:
February 5, 2021 at 12:26 pm
1) You can set up a trade as described in the chapter
2) Yes
3) 20 per executed trade
What is the exit Statergy in an arbitrage.
You close out the position, that\’s it.
CAN WE MAKE SYNTATHIC PUT WITH FUTURE LIKE CALL
Yeah, you buy a PE and sell a CE, it forms a synthetic put.
HI There,
I have been observing Put Call Parity for quite some days,
I do See it daily when the market makes a good move
I have 2 Questions?
Todays example:
CE 180
Strike 14900
PE 166
Future 14945
There is 31 point how i can encash It.
Is it possible to exit the trade before expiry?
How much will be the brokerage in zerodha?
1) You can set up a trade as described in the chapter
2) Yes
3) 20 per executed trade
sir can we do arbitrage trading in two future contract by buying this month contract and selling next month contract..is it work and can we make profit
Yes, you can, as long as there is an arbitrage opportunity.
\”Regarding this – such lame attempts to conceal an obvious mistake looks shameless, ——> I still don’t know where the mistake is.\”
If you still do not know where your mistake is, I am afraid zerodha has to look for a better trainer, who knows that an in the money put will always be pricier than an out of the money call. This is very basic knowledge. And you are not accepting your mistake even after people like I and S. K. Ahuja have pointed it out to you.
\’that an in the money put will always be pricier than an out of the money call\’ –
Market snapshot at –
Date : 3rd Dec 2010
Time : 13.53:35sec
Nifty 13151.95
Nifty DEC 13150CE – 272.2
Nifty DEC 13200PE – 236.25
What do you have to say about this?
Sir, with all due respect I would like to challenge you that the price mentioned by you is impossible, even after discounting \”function of many things – the rate at which the market is moving, time, demand, supply, interest rate, and volatility,\” –as mentioned by you. I am also a stock market professional and a trainer for the past 2 decades and a Chartered financial analyst. Please don\’t try to mislead new entrants and novices, just because you want to maintain your stance, which is absolutely wrong. Even our mythological Gods have made mistakes and to err is human. Just accept your mistake.
I just read the chapter, I\’ve mentioned the premium is 107 and not 127 as you\’ve mentioned. Secondly, SK Ahuja says, that the premium \’practically\’ will be 69, well how is this possible? End of the day 7400CE is an OTM, and whatever value it trades at – 69, 107, or even 127 is purely a function of time to expiry and the market situation at that point. Who knows, maybe there was a monetary policy and the market was looking up? Or maybe there was a state election outcome and the market was looking for a favourable outcome? The point is that there are multiple factors which can drive the price up, which I\’m sure you understand well.
Lastly, I gain nothing by misleading people, that has never been my intention.
It\’s true that some people never change for the better.
S.K.Ahuja says:
February 10, 2016 at 3:16 pm
your assumption that at 7389 nifty future and at the value of 7400PE @ Rs.80, the 7400CE can not be 127 Rs. It will be practically 69 Rs. You are calculating profit/loss at various levels of nifty expiry. In scenario one you are calculating 227 as loss. whereas in case of future the loss would be 189. In scenario 2 you are calculating 27 as loss. whereas in case of future the profit should be of Rs. 11. In scenario 3 you are calculating 0 as profit/loss. whereas in case of future the profit would be 38 . In scenario 4 you are calculating 173 as profit whereas in case of future the profit would be 211.
So in case of synthetic future strategy the P/L is always the same wherever the nifty expires. I would like to take note of the same and revert back if I am mistaken. Thanks.
Reply
Karthik Rangappa says:
February 10, 2016 at 3:32 pm
Why do you think the CE would not be 127 and why 69 specifically? Do remember that the payoff structure of synthetic long is similar to futurs @ it’s breakeven point. I would suggest you download the excel and work around with the numbers to get more clarity.
Reply
S.K.AHUJA says:
March 13, 2016 at 9:17 am
Very poor Mr. KARTHIK RANGAPPA, Shame on the Zerodha Varsity. Can you show me any trading screen any time in the history of stock market or in future, when NIFTY FUTURES trading AT 7389, the rate of the 7400CE to be 127 and 7400PE to be 69. YOU FORGOT THE FORMULA THAT PUT PREMIUM OF ANY STRIKE + NIFTY FUTURES MUST BE EQUAL TO THE STRIKE PRICE +CALL PREMIUM. Wherever any mismatch is there the arbitration opportunity arises and immediately encashed by some trader.
Karthik Rangappa says:
March 14, 2016 at 7:15 am
I’d suggest you download the excel once and look into the values once before concluding things. Thanks.
S. K. Ahuja is absolutely right. When someone points out a mistake, it should be accepted gracefully by the trainer and apologized for the mistake. That will increase the credibility of zerodha varsity in the eyes of the public. Giving an ambiguous answer like \”go and download on excel and work around with numbers before concluding things\” and such lame attempts to conceal an obvious mistake looks shameless, to say the least. Sorry
Sir, with all due respect, the premium is a function of many things – the rate at which the market is moving, time, demand, supply, interest rate, and volatility. So when someone says how can the premium be 127, well, that\’s the price market is quoting. When I asked the gentleman to download the excel and work with the numbers, it is only to make sure the understanding gets better.
Regarding this – such lame attempts to conceal an obvious mistake looks shameless, ——> I still don\’t know where the mistake is.
Hello Karthik,
Can synthetic futures be used as an replacement for long futures.
Is there any savings per lot with this?
Regards
Aniruddha
Yes, but there is no real reason to do that.
Is there any option to limit the risk for synthetic long future?
You can hedge this again with a CE or PE.
is this strategy can be used only if we are opting to hold it till expiry . couldn\’t it be done for intraday?
Its best if you hold this to expiry.
What will be the margin required in Zerodha for a synthetic futures. Will it be lesser than (naked call buy+naked put sell).
If you have a naked CE and PE sell, then that is a synthetic long right? The margins won\’t reduce for this position as there is still a directional risk.
Hey Karthik,
Do you think with the current regulations this strategy to be fruitful? We need to carry options till expiry and we have this \”physical settlement\” thing. I\’m just curious about the ROI. Also if the option is OTM (one of them) I came to know that Zerodha is asking for a small amount to be kept in the account balance, is it true?
Thanks in advance!
You can always exit the trade just before the expiry and not hold to expiry. Yes, the margins increase closer to expiry due to physical settlement.
Sir
It will be very helpful if a lecture on \’how to analyse option chain\’ will be added.
Analysis like recognising support and resistance through option chain, information on long unwinding and short covering etc whatever a trader can extract information through option chain.
Thanks in advance
Are you referring to this? https://zerodha.com/varsity/chapter/moneyness-of-an-option-contract/
Suppose Reliance spot is 2140 and future is trading at 2120
Then I Buy 1 lot of future, Buy 2160 Put and Sell 2140 Call
If there is a shoot up or fall down,
Scenario 1 Reliance shoot up to 2400, my put option will worth less and my call option will become deep in the money. Bid and Ask price difference is huge in deep in the money contract. So I forced to buy back call option at higher premium than actual premium.
Scenario 2 Reliance fall down to 1940, my call option will worthless and my put option will become deep in the money contract. Bid and Ask price difference is huge in deep in the money contract. So I forced to squire off put option at lower premium than actual premium.
In option simulator and theoretical aspect it is fine but in practical it is not working
How to avoid loss in that two scenarios
Thanks in advance
The assumption is that you will hold to expiry. Before expiry, there are bound to be differences.
Karthik, could you please suggest some commercially available and good softwares which you are aware of, which do the identification of this arbitrage opportunity ?
Also could you please give a rough idea as to how many point would get eaten up in the transaction charges (as per latest rulings existing in July 2020) if we use Zerodha? On to this charge, then i would have to calculate the interest costs of the margins for two legs (futures and shorting the Put).
I\’m not sure about the softwares. These are usually bundled as a package – identification and execution. Someone like Symphony Fintec may have this, but I\’m not sure about the effectiveness. Charges really depends on many factors – how many orders etc.
Manoj: Sir, Whats wrong if I opt far OTM synthetic call with future ? Say Current Yes Bank Future is 1157 & 1200 strike CE AND PE IS 7.2 AND 54.5 RESPECTIVELY. here Long Synthetic long + Short Futures = 54.5-7.2-43=4.3. . Is it not offering any arbitrage opportunity? You talked with only ATM in this regard.Please Explain Sir…..
Karthik: The trick is to make sure you are completely hedged out of the deltas when you initiate the position. With ATMs the call delta negate the put deltas. But with OTM it will not.
I was referring to the above two comments^
Vishal, I will get back on this.
Vishal, looks like you are right and I was wrong with my reply to Manoj. Yes, you can set this up with any strike, it should not matter.
Hi Karthik
Hope you\’re well. You had mentioned in one of the comments that the downside of initiating this arbitrage trade on OTM options is that you won\’t be delta neutral. But my question is why does that matter? Once you initiate this synthetic call + future arbitrage strategy and hold to expiry, your payoff is going to remain the same irrespective of the movement of the index? So being delta neutral doesn\’t really matter here? Or am I missing something?
Can you share the context in which I had stated that Vishal?
Great strategy. Thanks for putting it up in a lucid manner.
My query – would it make a better case in a market where the Futures are trading at a discount to Nifty cash, if we reverse the parameters ? I mean if we go long on Futures, short on the call (ATM) and Long on the Put (ATM).
I would request you to please upload an Excel Sheet for this calculation.
Also, may i request you to put the 50 gradations in the Nifty prices such as 10250, 10300, 10350, and so on in your excel sheets.
(Although even without these gradations, i remain grateful to you for offering ready-made excel sheets anyway.)
Yes, you can set this us when nifty is trading at a discount, but do make sure the discount is wide enough. You go long Fut and short the synthetic. Everything else remains the same 🙂
Okay , do let me know if you come to a conclusion.
Sure, will do. Intuition says it wont work 🙂
You said that this could be done even in weekly expiry.
But how could we do options in a weekly expiry when futures are traded in monthly expiry. As prerequisite of this trade is all contract should be of same expiry.
Ah, sorry that never occurred to me. This could be an issue. Need to spend sometime to think through this.
Hi Karthik,
You said in some comments above that it could be done in weekly expiry , but as far as i know futures are traded in monthly expiry so how could we short future of a monthly expiry and buying/selling weekly options as expiry was different.
Also could you enlighten me how synthetic long arbitrage is different from synthetic short arbitrage , further which one is to be followed ?
Thank – you !!!
The difference between synthetic long and short is just the directional play. I\’m not sure about the other query, can you please share some context?
Hi Karthik,
Can this strategy be used if we wish to close our positions, say a week before expiry of contracts?
Regards
Yup, you can.
If the price of the Put option is greater then the price of the call option when I\’m assembling the shynthetic long, I don\’t have a arbitrage situation? I just have the ability to purchase the call for free?
Thank you
Hmm, Call for free, yes, but the behaviour of the overall position is not that of a Call option.
Sir can you tell me how did you code Zerodha.Did you do it on your own or hired someon else.I want to do for my college project
Viraj, sorry, I don\’t seem to get your question. Can you please add more context?
So its better to take the trade when the fut is trading higher then the index yes like show in nifty screenshot?
Hmmm, not really but slightly more intuitive.
No reply if you want example you can check today\’s fut and index prices
How to trade with the arbitrage strategy
For this, you need to buy futures and sell the synthetic futures and hold to expiry. But practically this can be tricky to implement since the strike has to be around the price at which you\’ve gone long. Any variance can lead to losses.
Lower the trading value of index
Eg 20000 is index and fut is at 19980
Yes is this correct when we see fut trading under the index?
Under the index meaning?
Sir I was doing on bank nifty
On Friday BANKNIfty index is trading at 20970.10 and fut is at 20890 (80). Fut is trading lower than index
You said in any set of spread we should buy the low price and sell the higher price (arbitrage with two future)
Strike price is 20900 ce at 521.60 and pe at 543.50
I paper traded buying the ce and sell the pe (synthetic long) I got profit on 1 day and later on wards my profits turn in losses
Now my question is how to trade with this
Did you short the Fut and go long CE and short PE?
How to do arbitrage when fut is trading below the underlying asset (put call parity)
I mean we should do synthetic long or synthetic short?
You can sell stock and buy futures, Manoj.
Hello Karthik,
Is it possible to execute the synthetic future strategy to go long or short future at a desired strike price??
E.g. if I buy call and sell put on a strike of 9000 when nifty is 9900, wouldn\’t it be acting like I have went long on a future worth 9000??
Abhijeet, long CE and short PE at 9000 create a long futures position at 9000, not 9900.
can u elaborate on overall P&L.
Look at-in 3 parts –
1) How much did you make on your short futures position?
2) How much did you make on your short put position?
3) How much did you make on your long call position?
Net P&L is a sum of all the 3 above.
Today took a arbitrage trade on nifty it was a mock trade.nifty future short @10042.75.strike price 10000 nifty ce buy 280.35 pe short -256.8.of 25jun 2020 expiry.squared off 10 mins before closing bell .future buy @9973 cover short sell of ce at 242.75 and pe buy at288.20.incurred loss in the synthetic long strategy.what gone wrong in this trade?
This is expected…you make a loss on options position which is offset by the short Fut position. You need to look at the overall position P&L.
hello .very much excited after learning synthetic long strategy.my query is that should the strategy position to be held till expiry to get small guaranteed returns.under what conditions this strategy would make loss.
Yes, its best help to maturity. Loss occurs when the market goes down from the point you\’ve entered the trade.
Hi Karthik,
Again correct me if I am wrong,
1. I have gone through last few chapters and it took time to understand the logic of selling two OTM in Call Ratio Back spread, ultimately i read one of your comment, to adjust the delta the strategy is suggested to go long on two OTMs.
2. In this above chapter the strategy becomes delta neutral once we Short Future (Delta for ATM CE 0.5+ and Delta for ATM PE 0.5+ since we have shorted, total becomes 1 and adding futures will have a delta of -1= Hence total position Delta- 0)
Yes, thats right. Fut Delta = 1, add it to options to make the overall position delta 0.
sir this option stategy works in weekly option also….
Yes, across expiries.
Hello Sir , Hope ua doing well.
I want to know whats the current status of STT on exercising the rights.
I went through the link u gave.
Something has changed after September 19.
So does that effects what we have studied in this chapter.
Thank U Sir.
No more STT, did I share this link with you earlier?
https://zerodha.com/marketintel/bulletin/230019/no-more-stt-trap-on-exercised-options-from-today
Thank you sir for great lesson. Excellently explained with excel sheet. One questions, do we have Synthetic Short Arbitrage strategy?
Taking same strike prices and example, can we have a opposite strategy?
Short 7300 CE @ 79.5
Long 7300 PE @ 73.85
Long Nifty futures @ 7316
Sir, may be I\’m talking nonsense no expert like you. Please share your view.
Hi Karthik,
a basic question on options selling.. like margin requirement change in case of futures depending upon M2M, does the same happen with options (in case of shorting) ? If not then what is the rationale because for Option writers the risk/possibility of loosing huge sum of money is as good as a future short-seller
Yes, in case the position goes against, then the margin also increases.
HI KARTIK,
IT BECOMES DIFFICULT TO FIND AN ARBITRAGE CONDITION AND WE GET TIRED AND LOSE OUR CONCENTRATION. SO ANY SHORT CUT TO FIND THE SAME.
I AM LOOKING AT THE 2 PARAMETERS
1. WHEN THE PE PRICE IS GREATER THAN CE WHICH CONTRIBUTES TO THE SPREAD
2. PRICE OF FUTURE SHOULD BE MORE THAN STRIKE OF CE & PE (TO SELL FUTURE)
BUT BOTH THIS PARAMETER DO NOT MATCH AT THE SAME TIME.
SO CAN WE BUY 1ST PARAMETER WHEN THE CONDITION IS SATISFIED AND SELL FUTURE WHEN THE CONDITION 2 IS SATISFIED I.E. PRICE OF FUTURE IS MORE THAN STRIKE OF CALL & PUT(ATM)???
Unfortunately no shortcuts here. But you will have to find a programmatic approach to this, Denis. Doing it manually is not really possible I guess.
Hi Sir ,
In the NSE cross currency EURUSD is allowed ? as it there in the site , However in Zerodha has not been added this script .
Cross currency is allowed in India ? .
Thanks
Manas
Yes, but we don\’t have that yet on Zerodha.
Hi Karthik sir ,
My question related to synthetic long arbitrage .
Point the above attached excel sheet does not calculate the IV and in order to the correct Payoff one should put the correct IV if i am not wrong .
For an example
I have long 1 slightly out of money call Option with a IV of 50 = with the price of 250
and short a ATM money put option with a IV of 40 with the price of 270 . (Both for same expiry and same strike price )
and short one future contract .
Now as per the excel sheet
it not consider the iV and says on the expiry date the profit will be calculated based on the intrinsic value .
As per my finding ,i feel it will make loss if the IV will not remains same on the expiry date . Kindly clarify .
Thank you .
Manas, the synthetic arb is mainly to extract value from the mispricing. It is best you look at deltas and avoid IV here. Of course, you also need to ensure you are not buying a high IV premium and selling low IV. This is the only check you need to do with synthetic position.
Please can you explain why one would go with this option strategy when a futures long would give the same end result… and that too without any premium ?
Thanks.
In futures, your view is only in the direction of the market. However, with options your view can extend beyond the direction of the market, it can be on the speed at which the market is moving, time, and volatility.
Thank you for the prompt response,Sir.
I have one more question. I have used the excel sheet for synthetic long arbitrage trade and I have used closing prices of previous day. I have done my home work with Nifty and few stocks too. Now I want to enter into this strategy with those prices, but practically it is not possible because the prices change every millisecond and the net payoff too. It is practically not possible
Sir, how to trade these strategies in live market. Is there any method such that my trade will be profitable?
Hmm, Arjun there are two things that you can do –
1) Make sure your excel ticks live. To do this you need to know a bit of excel macros or programming
2) You can keep the excel ready and plug in the latest prices on the fly during the market hours.
Can you elaborate about bull box spread and bear box spread and create a excel worksheet for these strategies
These are extensions of synthetic position. Will probably write about it.
I hope you were not sarcastic with my wish of making 1.5% per month. Not all of us are gifted or competent to make 4-5% every day. That apart, you can paste any resource in your knowledge who can help in automating the trade because the premiums jump so quickly that the expected assured profit may be surpassed or may fall far below and even end in a loss. ATM BNF option can easily move 10 points in less than a minute. Wish at least basket order feature was available on kite. By the way the margin blocked is also much higher than the margin requirement shown on the margin calculator.
1.5% per month is an amazing return, which translates to 18% per year. If you can sustain this return for a few years, you are talking about serious money 🙂
Unfortunately, I do not know anyone who can help you with coding.
Very quick response indeed. I never expected that you will up so passionately that too during market hours. I executed one such bnf opportunity today and want to see it happen really. I think if I can get someone help me in writing a code for this and automating it, there will be no tension even if the monthly return is very low. Actually I was interested in this and had been searching on moneycontrol for quite sometime (cash-futures combo). But the problem was that the asset was never available at the prices it showed. Wish you write a story on automating and the costs involved in this. 1.5% per month without risk is also an excellent option in my perspective though many people aim to make more than 5% per day!
Unfortunately, I cant help you with this, Anugnani. Btw, 1.5% a month is incredible 🙂
I have downloaded the calculator and found that the same fixed arbitrage opportunity exists for any strike price (Not just ATM). The only condition is that the difference between the futures and spot should be greater than the debit required to take positions in options. I changed the strike prices however I like below the spot price (ATM Strike Price). Though the premium will not be same for the different strike prices, the point is that the pay off is fixed for whatever strike price we choose. If we change the strike prices to a value greater than the spot price (again assuming premiums are same which is not true in reality), then the pay off will be loss but fixed. I also did not understand if the short put is debit as mentioned by you. Is it not credit? I hope you will see this post and clarify though I am doubtful if you will read comments on something this old.
I need to evaluate this myself, Anuganani. From what I can gather, it does seem ok to me. By the way, you are right, all short positions is a credit, not a debit.
Hi Karthik,
I am trying to execute the Synthetic Long & Arbitrage strategy for the currently ongoing Nifty AUG Options & Futures.
I downloaded your excel sheet available at https://zerodha.com/varsity/chapter/synthetic-long-arbitrage/
Underlying Nifty
Spot Price (NIFTY 50) 11029
Long Call (ATM) (NIFTY AUG 11000 CE) 11050
Short PUT (ATM) (NIFTY AUG 11000 PE) 11050
Long Call Debit for Long Call 144.6
Debit for Short Put 129.55
Net Premium -15.05
Short Futures (NIFTY AUG FUT) 11012
As per the output the Net Payoff is coming to -53.05 but this strategy is supposed to yield a positive profit
irrespective of the market movement direction.
1. Why is the Net Returns negative? Am I missing something here?
2. How to execute this strategy to get profitable returns?
Thanks,
Rajkumar
1) The net +ve returns are based on the premiums available at the given moment. So +ve returns are not always a guarantee.
2) You have to time the premium for this.
Hi, sir I wanted to ask that are there any restrictions on the quantity of arbitrage like this, assuming there are unlimited opportunities (I know which is not possible in reality)? But still I wanted to know.
No, not really, Abhishek.
Hi Karthik
Under the key takeaway section you have shared Payoff Computation Excel sheet for Arbitrage opportunity using a “Synthetic Long + Short Futures”.
Request you to please upload the Payoff Computation Excel sheet for “Synthetic Short + Long Futures”.
I have done it, but will be great if you can also share the same, so that I can validate my calculations.
Thanks.
Nikhil
Ah, let me check that, Nikhil. Thanks.
Ok sir.
Can you please tell some stocks which are very liquid in options
Nifty index contract is the most liquid, Kavita. Apart from that, SBIN, TCS, RIL, Tata Motors etc have decent liquidity.
Sir, is stt completely removed now ??
No, but it became a bit simpler. Check this thread – https://tradingqna.com/t/no-more-stt-trap-on-exercised-in-the-money-options/18977
Sir is there any way by which we can get atleast 2 or 3 points arbitrage everyday ?? Like taking multiple positions in options like buying/selling calls/puts or maybe mixing futures with them if needed.
Ah, no one can guarantee you that, Kavita.
Hi Karthik
Request you to please upload the Payoff Computation Excel sheet for \”Synthetic Short + Long Futures\”.
I have done it, but will be great if you can also share the same, so that I can validate my calculations.
Thanks.
Nikhil
It is available in the chapter, look for it just after the key takeaways from the chapter.
Hi Karthik
In cases of weekly option expiry date, rather than the last thursday expiry, Will the Cost of Carry for Futures contract impact my Arbitrage profit? (Nifty or Bank Nifty)
In your example scenario and/or calculation excel, I assume in the example scenario, Options & Futures both have same expiry date.
But I was thinking, if I try this somewhere in the middle of the month, by squaring all positions, what will happen? Will I actually be able to book the profit as per computations? Or do we need to factor in any other parameter? (Cost of carry)
No, the actual profits may not match the excel, as the assumption is that you\’d hold to expiry. However, this should not restrict you from closing the position earlier. You can close it earlier if you think the opportunity is right.
HI Karthick,
What is the spread value in negative as per you excel, can i still go and execute the trade?
Yeah, you will have to pay attention to the long and short side of the trade.
I need bit clarity and let\’s talk with an example
Ref. data below as per your excel
Stock: INDIANB
Spot : 227
Long Call (ATM): 220
Short PUT (ATM): 220
Long Call Debit for Long Call: 56
Debit for Short Put: 5
Net Premium: -51
Short Futures: 227
Spread: (-44)
here as per my understanding i need to execute the trade as below
1. Buy CE @ 56
2. Sell PE @ 5
3. Sell INDIANB Future @ 227
In this case if i execute the trade i will gaining profit of Rs 44 on expiry or Loss?
On the option leg, you are long and you are short on the futures leg. Technically you are supposed to make the spread. The spread is 227 – 220 = 7. Not sure how you arrived at -44. I\’d suggest you use the excel sheet to see the overall payoff. Good luck!
Thanks Karthik for you prompt reply,
-44 is Spread output by your excel formula only (i didn\’t arrived my own)
Spread = (Short future – Strike Price) + Net Premium
Spread = (227-220)-51
Spread = -44
I confused again whether anything to be changed in excel calculation
Let me check this and get back to you again. Thanks.
A) Sir, is Arbitrage still working?
B) If incase i have a capital of Rs 10 lacs, can i get the Arbitrage benefits by earning 2-3% every month assuming (a) i select a particular stock on the start of the month the future of which trading approx 3% higher than spot price, (b) buying in cash and selling in future with same quantity, (c) Squaring both the positions on expiry i.e. last Thursday of the month.
C) Does convergence always happens at the expiry i.e. spot=future
D) What, if in the middle of the month stock rises to 20%, do i need to have an extra margin or the margin which was provided by Zerodha at the time of selling future will hold good till the expiry.
Hi Karthik, In futures you have demonstrated calendar spreads. Is it possible to perform such kind of strategies in options as well? for example, Assuming that IV s of May ATM options continue to increase up to the declaration of election results and assuming that IVs of APR ATM options will be more range bound between 13-15 up to expiry and knowing that the theta of Apr series is much higher than that of May series, is it possible to buy and ATM option of May series and sell an ATM option of Apr series.Its a perfect delta neutral strategy playing only on theta and vega. if such a strategy is meaningful, then how would the P&L diagram of the strategy look like and how would the strategy behave in the case of puts and in the case of calls?
Neehar, that\’s possible but gets a little complicated especially since options are not really a linear instrument. In my opinion calendar spreads (where only time matters) is best done with futures.
Understood.Thanks for your reply.
Cheers! Happy learning.
Hello Karthik,
how is margin calculated for the artibtrage trade using Long Synthetic long + Short Futures. The margin caculated togehter on all 3 trades or seperate margin is needed for each trade.
Simply does margin reduce as there is lesser risk in such a trade. I am using zerodha Kite.
Regards
Parag Joshi
The risk is set off and you get some margin benefit. Check this – https://zerodha.com/margin-calculator/SPAN/
Dear Sir,
Can this strategy be used on intraday basis?
Yup, you can. However, I\’d prefer to run this on an overnight basis.
Thank you Sir, for the clarification.
One followup question, kindly explain the reason for overnight trade?
My understanding, please correct me if wrong: In case of intraday, we can use BO&CO to trade, which means, we need less capital than overnight calls. Hence, returns will make sense.
Overnight because we give sufficient time for the trade to evolve and mature.
Got It! Thanks a lot sir.
Welcome!
Hi Karthik, can we use any strike of Call & Put (ATM, ITM or Deep ITM etc.) as long as strike is same for both call & put? Since after all, spot price moves out of the equation on expiry.
Sorry Himanshu, I need a little more clarity on your query. Can you please elaborate the query, thanks?
Hi Karthik. Since you wrote in above lesson to choose ATM strikes for put call parity arbitrage, I want to ask if we can choose any other strike like OTM, deep OTM or deep ITM for the put call parity arbitrage?
That may be a little tricky, Himanshu. Best to stick to ATM strike.
Ok Karthik. But as per your knowledge, do you think that at least in theory, its is logical to take Call & Put of any strike for PCP?
I\’ve always worked with ATM options, Himanshu.
Hi,. Karthi,. Have you heard about weirdor or jeep options strategy. Do you think it is a good strategy??
Ah, no. Maybe I will have to do some research on this. Thanks for letting me know.
Hi, karthi,
I just don\’t understand why the nifty puts at strike 3000, 4000 and 5000 are traded now.
If the buyer may hope for a fall,. But the seller is getting only around 1 rupees as premium which will be obviously very less than the normal interest rate for their margin. Why the sellers want to take this risk and sell it. Am I missing something?
Well, different opinions (especially on risk) is what really makes the market 🙂
sir what is the prolem if we take slightly OTM strike rather than ATM. Anyone\’s help would be appreciated.
There is no problem, but the deltas would vary a bit, so you;d need to adjust a bit which comes at a cost.
sir before expiry means day before expiry or you mean to say before end of the expiry??
It means, at any point before 3:30 PM on expiry day.
Sir , if future is in discount then short synthetic call and long future.. is it work???
Yes, as long as you have a valid arbitrage opportunity.
Sir i found 4 point spread in natural gas current and next month. Next month is coslty than current one. If i buy current month and sell next month, can i get all 4 point differnce at the day of expiry???
I doubt it, Gaurav. The 4 point spread could just be attributable to the cost of carry.
hii karthik,
can you tell me the approx margin requirement for the Synthetic Long & Arbitrage trade that you have demonstrated above?
You can always use this – https://zerodha.com/margin-calculator/SPAN/
I mean is it a good idea to keep around 1 lakh rupees blocked as a margin for such a small profit.
Depends on the time period within which you are expected to earn this profit 🙂
Hi Karthick,
How to back test an option strategy? How we can get price data for historically expired options?
I am looking to back test IRON Condor Strategy.
Backtesting options is a little tricky, Sadha. You will have to download the data from the bhav copy here – https://www.nseindia.com/products/content/equities/equities/eq_security.htm
Hi Karthick,
Thanks for your answers on option back testing.
I checked the nse bhav copy and that is of little help in what I need to do.
I like to back test and understand how the how the 3 strikes away OTM options loss its value when it reaches near expiry, in the bhav copy we can get only the BANK Nifty data but not the OTM option price data, Do you have any idea of how to identify the option price? For Example , Now I need to get the Price of CE 26800 of May 31st Expiry when it was trading on May 24 EOD, Like that, any help? Also you have mentioned Option Back Testing is little tricky, If you could provide a chapter or advice in OPtion back testing it would be great help and learning.
Thanks
Sadha
As time to expiry decreases, the probability of OTM option to remain as OTM increases, hence the rapid decrease in premium. By the way, I think you can search for contract/strike wise OHLC, check this – https://www.nseindia.com/products/content/derivatives/equities/historical_fo.htm
This NSE site dose not provide geniue tick by tick data for all strike prices. I request to zerodha, please provide tick by tick option pricing historical data to backtest this strategy before entering into real market.
You can access 1-minute charts on Kite.
Karthik,. Do you have any chapters for back testing? Expecially back testing option strategies.
No, unfortunately, nothing for now.
Hi Karthik, I tried to implement synthetic long arbitrage on nifty as of today using the template shared and net pay off was -0.05. Does that mean there is no arbitrage exists as of now in the market to implement this strategy or is there any error in my feeding the data into the excel?
Input Data
Synthetic Call with Future
Particular Value
Underlying Nifty
Spot Price 10767.65
Long Call (ATM) 10750
Short PUT (ATM) 10750
Long Call Debit for Long Call 106.05
Debit for Short Put 118
Net Premium 11.95
Short Futures 10738
Net payoff was -0.05 for strike from 10000 – 11700
Yes, Sumit. There seems to be no arb here.
Thanks Karthik!!
Welcome, Sumit. Good luck!
Sir, how\’s a discount broker different than other brokers ?
By definition, a discount broker offers deep discount on execution services whereas a full-service broker offers research and higher brokerage. As you may know, Zerodha was the first broker in the country to introduce discount broking. Since then we have moved away from just a deep discount platform to a more advanced tech platform. We have many other services including Varsity which is given out to clients.
Dish TV cash market share buy purchase = 74.75 of 7000 shares
FUT Jun contract sell 75.35
If I closed both positions on expiry of june….then what will be my profit loss?
So you will make 60 paisa per share here.
Dear Sir,
(1) Is there any strategy for trading futures with options? (except buy 1 fut & buy 2 PE ,etc)
(2) What are the 4 legs of box strategy?
Thanks
1) You can combine futures in many ways, really depends on what you are looking at
2) Buy Call, sell put of one strike and sell call and buy put of the next strike is a 4 leg box.
Can you provide any online portal or weblink or book which provides various future strategy with Options?
I need to dig into this, Prakul.
Sir, why would someone like to have a futures payoff instead of buying simply a call option ; at least in the latter case the loss will be limited to the premium ?
True, but option P&L is dependent on many other variables like market direction, volatility, time, speed, etc. In contrast, futures payoff is directly related to the directional movement in the market.
Can you clarify between arbitrage, hedgin and jobing?
Arbitrage involves buying and selling the same asset simultaneously across two different markets, with an intention to make a risk free or relatively low-risk profit.
Hedging is when you want to protect your Portfolio or position\’s P&L against adverse market movement. You don\’t expect to make a profit or loss when you hedge, more on this here – https://zerodha.com/varsity/chapter/hedging-futures/
Jobbing is when you buy and sell large quantities of shares for a quick profit, this is done on an intraday basis.
You buy call and either sell fut or sell equity ,is there any possibility to price difference and grab it ,is it arbitraging or not?………..And what is a future scope of arbitrage opportunity if algo software comes in picture and technology improve
It is a sort of an arbitrage if you Buy spot and sell Fut. I think the abr opportunities (especially the ones which involves fast information flow) is kind of diminishing simply because systems are getting faster and faster shrinking the opportunity universe.
Hi Karthik,
When will I be able to earn profit as per showing in excel. let\’s say I calculated current spread and it is 20 rs. and I opened a position. So when will I earn this? Do I need to keep this position open till expiry to earn Rs. 20 profit ? And what would be profit/loss on expiry day? Is it difference of spread on expiry day while closing position or 20 Rs. flat on expiry ?
Ideally, these positions have to be open until expiry to take full benefit of the spread.
Thanks Karthik. Really appreciate.
Cheers!
I am a great fan of Karthik Rangappa and Varsity. Tried to create a google excel sheet which will get automatically update every 1 hour to find these kinds of opportunity. If interested people can refer to https://docs.google.com/spreadsheets/d/15jfqSqHcdAFAY_Ca1bXL5MVtHZ42Z1fxICadzLJSaFw/edit for more information.
Sir about Box Spreads. Have you ever been able to successfully execute it? Also, can you give me some pointers regarding the execution of Box strategy and other such Execution risk involved arbitrage strategies?
Yes, I\’ve done that couple of times. Very cumbersome since it involves 4 legs. A lot of execution risk as well.
Sir is it possible to create an arbitrage opportunity by entering into Call, Put and Futures at different points of time? For example, the option prices are always high in beginning of contract so short the put option then, and as time passes, buy call option and futures at a lower price? Would that be possible? I know that it is not possible to predict option movements, but what do you think of this sir?
Thanks in advance.
Yes, in fact, there is something called as a box strategy, involving 4 option legs which mimic 2 futures trades. Sort of an arbitrage, do check it out.
First of all, thanks for the reply sir. From what I understand, it is possible to create an Arbitrage opportunity and that the box trading system is a limited and risk free profit strategy. May I ask, what are some others strategies like this one, or which book deals with them?
Yes, the risk in box is execution risk. Assuming you execute the trade at the right prices, you can capture the risk-free profit. I\’d suggest you take a look at Option pricing and Volatility by Sheldon Natenburg
Sir that was a fascinating book and thanks for the recommendation. I have two questions 1.Have ever executed the box strategy and what can you say about that? 2. If we manage to convert it into an automated trading system, it would be like you said, a money machine, or am I missing something?
Well, automation needs exchange approvals 🙂
Sir thank you so much for pointing me toward option volatility and pricing, it was a treasure. I have developed a trading system based on Box strategy. However, I have not done this before and am having problems with backtesting the same. What do you suggest I do now? Thanks in advance.
Backtesting is essential, otherwise, it\’s like driving a brand new car, without knowing where the gearbox or breaks are. So do backtest or at least get an insight into its behavior. In the worst case, take it live, with small quantities and scale it over time.
An ITM option will always expire at a price lesser than the intrinsic value. So arbitrage won\’t work.
It will be settled at IV, but accounting for STT and charges, it will be lesser than IV.
Dear Nitin sir,
is it a good strategy to long future of nifty and sell corresponding call and vice versa as strategy equivalent to stock backed call or will it be naked risky to do so.
Regards and thanks,
shafik s
Naked options are always risky. If you are not willing to expose yourself to so much risk, then yes, hedging is a good practice.
Thank you very much for reply.
Cheers!
Dear Karthik,
Is there any way I can buy and/or sell more than one CE or PE at the same time using Kite Web or Kite Android? e.g. buy one ATM Call, sell one ATM put and sell one future in a single order or do I have to do it one after the other?
Thanks and regards,
Samir
I\’m afraid you will have to do it sequentially.
You can use 3-Leg order on Zerodha Nest Trader Software.
Hmm, I need to check up.
can you help to make exel sheet for USDINR OPTION
We have put out the excel sheets already.
Today I stimulated arbitrage in nifty and as per excel sheet it is showing 19.4 as pay off then what will be the total amount of profit after costs considering m a zerodha client brokerage
And how much margin required?
Check this – https://zerodha.com/brokerage-calculator
Please check this – https://zerodha.com/brokerage-calculator
Hello Sir
These are the last lines in the above chapters.
\”So considering these costs, the efforts to carry an arbitrage trade for 10 points may not make sense. But it certainly would, if the payoff was something better, maybe like 15 or 20 points. With 15 or 20 points you can even maneuver the STT trap by squaring off the positions just before expiry – although it will shave off a few points\”
For options we can exit by buying back the sold share or selling the already bought share just before few minutes of the expiry to get off the STT trap but however how can we exit from the futures contract? As it will end on the expiry day itself. So what I understood by your words \”although it will shave off a few points\” is because of the futures contract we cannot alter/change/modify/exit. Is my understanding in both the points right? Please clarify.
Thank You
You can exit all derivatives positions before expiry if you wish too. However, it certainly makes sense to exit the ITM options before expiry for reasons stated here – http://zerodha.com/z-connect/queries/stock-and-fo-queries/stt-options-nse-bse-mcx-sx
But do note, futures position is not affected by STT. So you can continue to hold them to expiry.
Dear Zerodha,
Please explain iron butterfly and condor with example. I am not able to find anything on varisty, however its has been mentioned in orientation that we will explain.
Regards
Nitesh Kumar
Will try and add those chapters soon. Thanks.
Does this strategy only work upon expiry….what if we decide to square off before expiry?
You can choose to sq off earlier and book your profit or loss.
Hi Sir,
1) If by using option strategies my net payoff is 0 or -ve, would then also STT charges be applicable?
2) Are the STT charges same in case of futures ?
Yes, STT is applicable. Check this – https://zerodha.com/charges
Dear Sir, If I sell next series future and buy this series future. can I keep premium difference at expiry. What are drawbacks in this strategy.
You can keep the premium provided there is a case for it. Drawback is execution risk.
Hi Karthik, a small doubt,
will the pay off be the same if we do the reverse of this strategy like (synthetic short + long futures)
where as synthetic short= short CE &long PE. IS THIS POSSIBLE??. correct me if i am wrong.
Thanks&Regards
Yes, absolutely. The payoff will be there as long as there is an arbitrage opportunity. Synthetic long = Long CE + Short PE. Synthetic Short = Long PE+ Short CE
Hello, thanks for explaining these strategies in such a simple way. Just have a query on arbitrage – Since BankNifty has a weekly options contract so going by today\’s date i.e. 11th Aug 2016, BankNifty 11th Aug will be expired today. Suppose as per your strategy I buy a lot of CE at strike price of 18600 (ATM) and sell a lot of PE at the same strike price and also short BankNifty futures at current price. Now future is going to expire on 25th Aug so if i execute the above trades, options will be expired today but if i square off my future trade also is it going to give me the same result? Hope my question is clear to you 🙂
Manoj, if you are executing this with an intention of capturing an arbitrage, then its important to close all the positions on the designated date – which in this case happens to be the Bank Nifty\’s weekly expiry. So you got to square off the futures position on this date as well.
Got it… thanks a ton
welcome!
Sir, Whats wrong if I opt far OTM synthetic call with future ? Say Current Yes Bank Future is 1157 & 1200 strike CE AND PE IS 7.2 AND 54.5 RESPECTIVELY. here Long Synthetic long + Short Futures = 54.5-7.2-43=4.3. . Is it not offering any arbitrage opportunity? You talked with only ATM in this regard.Please Explain Sir…..
The trick is to make sure you are completely hedged out of the deltas when you initiate the position. With ATMs the call delta negate the put deltas. But with OTM it will not.
After 2 trading sessions future is 1152 compared with 1157. 1200 CE – 5.00 compared with 7.2 and PE – 38 compared with 54.5. Sir whats the logic behind it then?
Logic as in? For the premiums to vary?
Mr. Karthik, I have read almost all your modules and no doubt you are doing excellent by explaining in & outs of stock market in details. I really appreciate your efforts. But I have one doubt. In arbitrage set up, Scenario 1: Nifty expired 7200. Means nifty spot 7200. You considered we short Nifty futures at 7316 when Nifty spot was 7304, means there is 12 points difference in Futures price. When you considered nifty closed at 7200 then you subtracted Nifty spot price i.e. 7316-7200=116??. But when spot is at 7200 futures must be at 10 to 12 points more. Considering Nifty futures 10 points more, the final equation for P/L will become like this -79.5 – 26.15 + (116-10) = 0.35. Which looks worthless. Please guide if I am thinking wrong. Thanks.
Thanks Swapnil.
Upon expiry, the spot price and futures price will always converge, hence the arbitrage works 🙂
Super.
Hi kartik,
If I sell nifty future at 7500 on Monday and on Tuesday market opens at 7400 and on opening I close my position. Then can I get benefit of rs.100. I.e 100*75=7500 per lot???????
Yup, you can!
This means I we are trading in future we cannot get benefit of gap up/ gap down????
Gap up or down is a directional aspect, you will get benefit of this. In futures you will experience it via MTM and in options the Delta will do the trick for you.
Hi kartik,
Since I learn in futures module, in future MTM position closes daily and broker buys next day.
So in future can we get benefits of gap up or gap down , since we get such benefits in option world.
No MTM in options!
Hi kartik
Very very thanks for clearing my doubts on option writing.
I have send friend request to you on Facebook. I am glad if you accept.
I\’m not so active on FB, but you can certainly look me up on Twitter, handle is @ZVarsity . Thanks.
sir,whats this kite is different from zerodha trade which we r currently using in our mobiles if its different&advanced how can we use in mobiles pls clarify mydoubt
I would suggest you use Kite Android App (which will be released shortly) to experience the difference 🙂
Hi kartik
Is kite app contains bo&co order type with trailing stoploss. If yes it makes mobile trading mush easy and efficient.
Not as of now, but eventually this will happen.
Is there any automated software that can let me know the arbitrage opportunity live. Because EOD prices may or may not be relevant on the following day. If available what will be the approximate cost. Or any info about who sells such software. Using Excel and nseindia will not be of much use because the prices are too delayed.
Lakshmi – not sure who provides this. If you are familiar with coding you can build this yourself very easily using Kite Connect APIs – https://kite.trade/docs/connect/v1/
sir can we select an ITM strike for an arbitrage trade ……???
Its best done with ATM, but you could give it a shot with ITM strikes.
Please guide. Taking real market example.
4 Feb close
IDBI Spot rate is 55.90
Feb future 5.2% discount 52.9
March future 8.9% discount 50.85
what If I buy March fut @ 50.85 and immediately sell Feb Future @ 52.90
so untill expiry day of feb I am safe.. No profit or loss can happen..as covered both short and long side..
But what will happen on expiry day ?
As feb expiry has to happen with the spot rate which is way higher than feb future ?
What strategy Can I use to shift on expiry day and pocket the difference between these two futures..?
Pls guide. Need to understand what\’s happening here ..
On the day of expiry in Feb, the spot and Feb futures will converge to a single point, this does not guarantee the convergence of March futures, so this is a bit tricky. I\’d suggest you wait for sometime, I will be discussing Calendar spreads and the technique to do this in sometime.
Hi kartik
Appropriately, almost for all nifty options the premium was roughly rs.35000. So in a trend please suggest me whether it is wiseful to write a deep itm option and collecting big premium in single trade or
Selling atm option for every 100 fall then exiting position and writing next ATM option and then exiting and so on doing when the trade lasts
Or whether premium declines more fast in otm or deep otm
Please give me most profitable way of trading option
See unfortunately there is no 1 strategy that suits all, everyone has different risk reward perspective and hence what works for me will never work for you or vice versa. Trading requires a lot of experimentation, I\’d suggest you keep this experimentation with small amounts of money that you can afford to lose.
Sir, What is the advantage of only synthetic long? by this we are taking loss and profit both unlimited. Just long call is having unlimited profit and limited loss. I think it is advisable to use with short future to get advantage of arbitrage as you’ve explained?
Secondly, to maximise the profit the difference between strike price and future price shall be more and difference in the premium of the CE AND PE shall be minimum. (future price-strike price -(ce premium- pe premium) = 7316-7300 – (79.5-73.85) = 16 – 5.65 = 10.35)
So it means when the future price is at the middle of two strike price them the return may be maximum. pl. correct.
Thanks
On its own the Synthetic Long is just like futures. But you can use this to identify and structure an arbitrage trade (as explained in the chapter). The calculation you\’ve shown is somewhat similar…leads to the identification of max P&L.
Hi kartik
Since margin required for option selling is same as that of futures and not on premium. So, selecting which strike price yields maximum profit for option seller, whether it is deep otm, otm, ATM, itm or deep itm ??????
The further you move away from ATM, the higher is your safety and lower is the profits. It is upto you to identify a sweet spot and write that option. I\’d suggest you use the Normal Distribution technique to identify the strikes.
The margin for selling options differs from strike yo strike. It reduces as go out from deep ITM to ATM and OTM and Far OTM.
Sir, isnt calender spread a sort of arbitrage then.. we spot the mispricing of 2 different expiry dates.. sell current month expiry and buy far month..?
Yes, CS is a time based arbitrage, in fact the most popular arbitrage technique.
Few minor corrections in the uploaded excel sheet.
In the tab \”Strategy\”
Cell C7 mentioning as \”Short PUT (OTM)\” i think it need to be \”Short PUT (ATM)\”
Cell G15 mentioning as \”PE_IV (OTM)\” i think it need to be \”PE_IV (ATM)\”
Cell C37 mentioned as \”LS – IV (ITM)\” it has to be \”CE_IV (ATM)\” with proper definition on cell D37
Cell C39 mentioned as \”HS_IV\” it has to be \”PE_IV (ATM)\” with proper definition on cell D39
In tab \”Synthetic Call with Futures\”
Cell C11 mentioning as \”Long Futures\” it has to be \”Short Futures\”
Cell G15 mentioning as \”PE_IV (OTM)\” i think it need to be \”PE_IV (ATM)\”
Cell C37 mentioned as \”LS – IV (ITM)\” it has to be \”CE_IV (ATM)\” with proper definition on cell D37
Cell C39 mentioned as \”HS_IV\” it has to be \”PE_IV (ATM)\” with proper definition on cell D39
All fixed, thanks for pointing these out 🙂
Hi kartik
Very very thank to you for clearing my doubts about option selling.
Clearly it make sense to buy option when premium is less and to write option when premium is high
True that!
Hi Kartik ,
The question is how does one execute the parity trade simultaneously across CE PE n futures . I mean fluctuations happen in milliseconds
There are few opportunities that exist for few over few seconds. I guess its best if you can run a program to keep track of this.
when option strategy module will be available in pdf format like other modules are available?
how many more chapters are left?
Rohan, the module is work in progress. I suppose another 8 chapters to go. Once this is done we will have the PDFs ready.
Sir, can you please send the link to download the PDF format for options?
Scroll to the bottom of this page to find the PDF download link – https://zerodha.com/varsity/module/option-strategies/
what is fun for a gain of 10 to 20 rupees by investing margin of 2 lot ie 1 for future sale and 1 for put sell.appx about 90000 to 1 lacs.
Well, a lot of professional traders like to take up trades where there is complete visibility on the downside risk even though the reward is limited.
Hi kartik
If nifty call option has premium rs.1 then how much money required to short one lot
Margins for writing options is usually same as that of the margins required for futures. The premium value is not really considered.
with 0% risk can we earn profit in option?
No risk, no return ! However you can minimize risk by using strategies such as Synthetic Long
Sir
it look very nice stratergy . but can you explain when is the right condition to enter the trade… what are the parameter i need to consider before entering this trade???
Mahesh, you spot it ..you execute it!. There is nothing like an ideal condition for this strategy.
thank you sir 🙂
Welcome!
your assumption that at 7389 nifty future and at the value of 7400PE @ Rs.80, the 7400CE can not be 127 Rs. It will be practically 69 Rs. You are calculating profit/loss at various levels of nifty expiry. In scenario one you are calculating 227 as loss. whereas in case of future the loss would be 189. In scenario 2 you are calculating 27 as loss. whereas in case of future the profit should be of Rs. 11. In scenario 3 you are calculating 0 as profit/loss. whereas in case of future the profit would be 38 . In scenario 4 you are calculating 173 as profit whereas in case of future the profit would be 211.
So in case of synthetic future strategy the P/L is always the same wherever the nifty expires. I would like to take note of the same and revert back if I am mistaken. Thanks.
Why do you think the CE would not be 127 and why 69 specifically? Do remember that the payoff structure of synthetic long is similar to futurs @ it\’s breakeven point. I would suggest you download the excel and work around with the numbers to get more clarity.
Very poor Mr. KARTHIK RANGAPPA, Shame on the Zerodha Varsity. Can you show me any trading screen any time in the history of stock market or in future, when NIFTY FUTURES trading AT 7389, the rate of the 7400CE to be 127 and 7400PE to be 69. YOU FORGOT THE FORMULA THAT PUT PREMIUM OF ANY STRIKE + NIFTY FUTURES MUST BE EQUAL TO THE STRIKE PRICE +CALL PREMIUM. Wherever any mismatch is there the arbitration opportunity arises and immediately encashed by some trader.
I\’d suggest you download the excel once and look into the values once before concluding things. Thanks.