7.1 – Expected returns

The next two chapter will be very insightful, especially for people who have never been familiar with portfolio techniques. We will venture into the realms of expected return framework and portfolio optimization. Portfolio optimization in particular (which we will discuss in the next chapter) is like a magic wand, it helps you decide how much to invest in a particular stock (within a portfolio) so that you achieve the best possible results in terms of risk and return. These are topics which the high priests of finance prefer to keep for themselves, but today we will discuss them here and truly work towards democratizing quality financial knowledge.

But please note, to best understand the discussion here, you need to have a sense of all the things we have discussed over the previous couple of chapters. If you have not read them yet, please, I’d urge you to read them first. This is good quality information and you would be a better market participant if you simply spent few hours reading them. The excel sheet used here is a continuation of the one used in the previous chapters.

So assuming you are all set, let us get started.

It is time we put the portfolio variance to good use. To begin with let us take a good look at the portfolio variance number calculated in the previous chapters –

What does this number tell you?

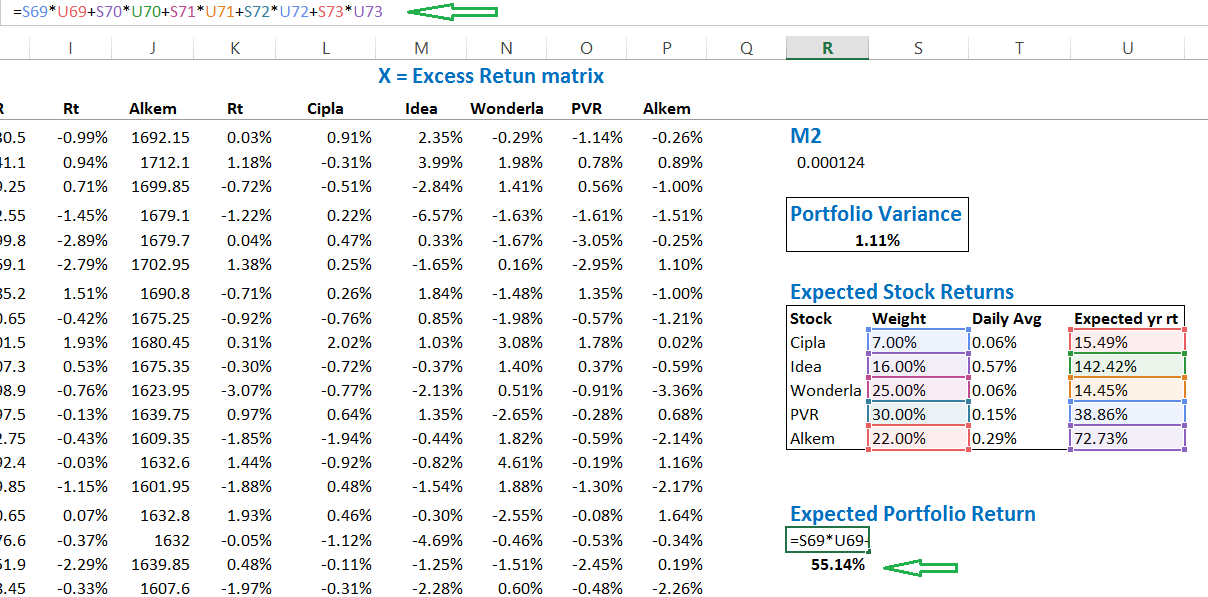
The number gives you a sense of the degree of the risk associated with the portfolio. Remember, we worked on the daily data, hence the Portfolio Variance of 1.11% represents risk on a daily basis.

Risk or variance or volatility is like a coin with two faces. Any price movement below our entry price is called risk while at the same time, the same price movement above our entry price is called return. We will soon use the variance data to establish the expected range within which the portfolio is likely to move over the year. If you’ve read the Options module you will probably know where we are headed.

However, before doing that, we need to figure out the expected return of the portfolio. The expected return of the portfolio is simply, the grand sum of the average return of each stock, multiplied by its weight and further multiplied by 252 (number of trading days). In simple terms, we are scaling the daily returns to its annual return, and then scaling it according to the investment we have made.

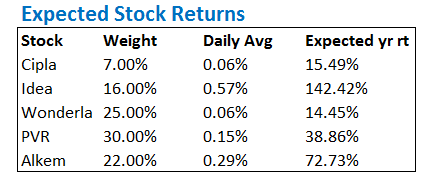
Let us calculate the expected return for the portfolio that we have, I’m sure you will understand this better. To begin with, I’ve lined up the data as follows –

The first 3 columns are fairly easy to understand I suppose. The last column is simply the multiplication of the daily average return by 252 – this is a step to annualize the return of the stock.

For example (Cipla) – 0.06% * 252 = 15.49%.

What does this mean? For a moment assume, I have invested all the money in just Cipla and not other stocks, then the weight of Cipla would be 100% and I can expect a return fo 15.49%. However, since I’ve invested only 7% of my capital in Cipla, the expected return from Cipla would be –

Weight * Expected Return

= 7% * 15.49%

=1.08%

We can generalize this at the portfolio level to get the expected return of the portfolio –

Where,

Wt = Weight of each stock

Rt = Expected annual return of the stock

I’ve applied the same formula for the 5 stock portfolio that we’ve got, and here is what we have –

At this stage, we have arrived at two extremely important portfolio parameters. They are the expected portfolio return which is 55.14% and the portfolio variance which is 1.11%.

In fact, we can scale the portfolio variance to represent the annual variance, to do this we simply have to multiply the daily variance by Square root of 252.

Annual variance =

= 1.11% * Sqrt (252)

= 17.64%.

We will keep both these important numbers aside.

It is now time to recall our discussion on normal distribution from the options module.

I’d suggest you quickly read through the ‘Dalton board experiment’ and understand normal distribution and how one can use this to develop an opinion on future outcome. Understanding normal distribution and its characteristics is quite crucial at this point. I’d encourage you to read through it before proceeding.

Portfolio returns are normally distributed, I’ll skip plotting the distribution here, but maybe you can do this as an exercise. Anyway, if you do plot the distribution of a portfolio, you are likely to get a normally distributed portfolio. If the portfolio is normally distributed, then we can estimate the likely return of this portfolio over the next 1 year with certain degree of confidence.

To estimate the return with certain degree of confidence we simply have to add and subtract the portfolio variance from the expected annualized return. By doing so we will know how much the portfolio will generate or lose for the given year.

In other words, based on normal distribution, we can predict (although I hate using the word predict in markets) the range within which the portfolio is likely to fluctuate. The accuracy of this predication varies across three levels.

• Level 1 – one standard deviation away, 68% confidence
• Level 2 – Two standard deviation away, 95% confidence
• Level 3 – Three standard deviation away,99% confidence

Remember, variance is measured in terms of standard deviation. So it is important to note that the annualized portfolio variance of 17.64% is also the 1 standard deviation.

So, 17.64% represents 1 standard deviation. Therefore, two standard deviation is 17.64% * 2 = 35.28% and 3 standard deviation would be 17.64% * 3 = 52.92%.

If you are reading this for the first time, then yes, I’d agree it would not be making any sense. Hence it is important to understand normal distribution and its characteristics. I’ve explained the same in the options chapter (link provided earlier).

7.2 – Estimating the portfolio range

Given the annualized variance (17.64%) and expected annual return (55.14%), we can now go ahead and estimate the likely range within which the portfolio returns are likely to vary over the next year. Remember when we are talking about a range, we are taking about a lower and upper bound number.

To calculate the upper bound number, we simply had to add the annualized portfolio variance to the expected annual return i.e 17.64% + 55.15% = 72.79%. To calculate the lower bound range we simply have to deduct the annualized portfolio variance from the expected annual return i.e 55.15% – 17.64% = 37.51%.

So, if you were to ask me – how are the returns likely to be if I decide to hold the 5 stock portfolio over the next year, then my answer would be that the returns are likely to fluctuate between +37.51% and +72.79%.

Three quick question may crop up at this stage –

1. The range suggests that the portfolio does not lose money at all, how is this even possible? In fact, the worst case scenario is still a whopping +37.51%, which in reality is fantastic.
   1. True, I agree it sounds weird. But the fact is, the range calculation is statistics based. Remember we are in a bull market (April – May 2017, as I write this), and the stocks that we have selected have trended well. So quite obviously, the numbers we have got here is positively biased. To get a true sense of the range, we should have taken at least last 1 year or more data points. However, this is beside the point here – remember our end objective is to learn the craft and not debate over stock selection.
2. Alright, I may have convinced you on the range calculation, but what is the guarantee that the portfolio returns would vary between 37.15% and 72.79%?
   1. As I mentioned earlier, since we are dealing with level 1 (1 standard deviation), the confidence is just about 68%.
3. What if I want a higher degree of confidence?
   1. Well, in this case you will have to shift gears to higher standard deviations.

Let us do that now.

To calculate the range with 95% confidence, we have to shift gears and move to the 2^nd standard deviation. Which means we have to multiply the 1 standard deviation number by 2. We have done this math before, so we know the 2^nd SD is 35.28%.

Given this, the range of the portfolio’s return over the next 1 year, with 95% confidence would be –

Lower bound = 55.15% – 35.28% = 19.87%

Upper bound = 55.15% + 35.28% = 90.43%

We can further increase the confidence level to 99% and check the return’s range for 3 standard deviation, recall at 3 SD, the variance is 52.92% –

Lower bound = 55.15% – 52.92%% = 2.23%

Upper bound = 55.15% + 52.92% = 108.07%

As you may notice, the higher the confidence level, the larger the range. I’ll end this chapter here with a set of tasks for you –

1. Plot the frequency distribution for this 5 stock portfolio – observe the distribution, check if you see a bell curve
2. We are dealing with the range for a year, what if you were to estimate the range for 3 months, or maybe 3 weeks? How would you do it?

It will be great if you can attempt these tasks, please do leave your thoughts in the comment box below.

You can download the excel sheet used in this chapter.

---

Key takeaways from this chapter

1. The returns of the portfolio is dependent on the weights of the individual stocks in the portfolio
2. The calculate the effect of an individual stock on the overall portfolio’s return, one has to multiply the average return of the stock by its weight
3. The overall expected return of the portfolio is grand sum of the individual stock’s returns (which is scaled by its weight)
4. The daily variance can be converted to annualized variance by multiplying it by square root of 252
5. The variance of the portfolio which we calculate is by default the 1^st standard deviation value
6. To get the 2^nd and 3^rd SD, we simply have to multiply it by 2 and 3
7. The expected return of the portfolio can be calculated as a range
8. To get the range, we simply have to add and subtract the variance from the portfolio’s expected return
9. Each standard deviation comes with a certain confidence level. For higher confidence level, one has to look at moving higher standard deviation