Maths made the modern world
For most of our history, the future seemed inscrutable. People believed that mysterious forces controlled their lives — fate, destiny, demons, spirits, whatever. One could placate them, but understanding them was impossible. Life was inherently chaotic. Anything could happen, to any one, at any time. All bets on the future were blind bets.
This isn’t true of the modern world. As Peter Bernstein explains in Against the Gods, we’ve mastered risk. We still can’t predict the future, but we can anticipate it. We can manipulate and fine-tune the challenges it brings; we can break risk into pieces, trading away what we don’t like and doubling down on what we do. That is, after all, what capital markets are for. Our mastery of risk lets us make bigger bets on the future, and survive them.
This is a mathematical achievement. Before we got here, we had to condense abstract ideas like chance and luck into mathematical form. We had to reduce the world into numbers, and learn how to work with them. Only then could we even think of risk in any meaningful way.
This is the story of 500 years in that journey. At its start, Europe had just come across a powerful number system from India. Over the centuries, it learnt to work with the system, and then added two original contributions of its own — probability and statistics.
With these new tools, people learnt to change the future. Of course, they don’t help us foresee future events. Using them, however, we can change how these events pay off. In a sense, this lets us control the effects of the future. Our system of dividing pay-offs, which was born in this 500-year period, is modern finance.
The boy that loved Indian numbers
Europe used the ‘Roman’ numbering system until mid-way through the last millennium. The system repurposed the Latin alphabet to symbolise numbers. 1 was written as ‘I’, 5 as ‘V’, 10 as ‘X’, and so on. By medieval times, Europeans had special symbols for numbers all the way up to 2,000. These made decent short-hands for numbers that one used regularly. For mathematics, though, they were clunky and inefficient.
A better system had already been devised here, in India. It centred on the innovation of zero – a number that meant nothing. Ancient Indians used zero, with nine other symbols, in a ‘positional notation’ system: where the position of a digit was key to its value. This is why ‘14’, for instance, is entirely different from ‘41’. The system was endlessly flexible. Just ten digits could make any number one could imagine, and their simplicity let people do complex calculations in their heads.
Try it for yourself: add LXVII to XXXVIII. Now add 67 to 38. See the difference?

Source: Picryl
When India met the Islamicate world, this number system spread outwards. More innovations, like fractions and decimals, were added along its way. The Arabs found new applications for it, in problems of navigation and commerce. The Europeans were far away from this intellectual churn, though. They remained mathematically stunted.
It was in these times that a young Italian boy, Fibonacci, accompanied his father to the beautiful Algerian port town of Bugia (modern day Béjaïa). While there, he was sent to an Arab master for a few days, to learn calculation. The master showed him the Indo-Arabic numbers, and all the ways they could be manipulated. The boy was stunned. As he grew older, he travelled across the Mediterranean for business, and sought mathematical knowledge wherever he went. The more he travelled, the clearer it was: this system was uniquely powerful.
In 1202, he condensed everything he learnt into fifteen chapters — in the Liber Abaci, or the Book of Calculations. The book was a masterpiece. It introduced its pre-mathematical audience to the Indo-Arabic system, showed how it worked, and then displayed the extraordinary ways in which it could be used. It dealt with some abstract problems — one of which famously gave the ‘Fibonacci sequence’. But it was also full of practical maths that would be useful for a merchant — how to calculate profit margins, convert weights and measures, calculate interest and more.
Source: Wikimedia
Liber Abaci was distributed widely through Europe. While it introduced the Indo-Arabic system to Europe, however, it would be centuries before Europe actually accepted the system. It was too heretical; too foreign. Decades passed. Fibonacci’s impact slowly faded.
Nevertheless, Liber Abaci introduced Indian mathematics to a new continent — one that was heading into a golden age. There, it was nurtured by the printing press, the Renaissance, the Scientific Revolution, the Enlightenment, and the explosion of global commerce. Like their predecessors, the Europeans would leave their own imprint on the system, giving it powerful new capabilities. Many of these are foundational to our modern world.
The friar, the gambler and the birth of probability
Three centuries after it was first released, Liber Abaci was largely forgotten. Fibonacci’s methods, however, survived in Italy’s abacco schools, which taught the region’s aspirational middle class. The schools were meant to create future merchants, accountants and clerks — people whose future occupations required extensive calculation. For this, they had developed their own mathematical tradition, using the Indo-Arabic number system. Towards the end of the fifteenth century, an Italian friar and teacher, Luca Pacioli, compiled the best insights of this tradition into another masterpiece: the Summa de Arithmetica.
As a friar, Pacioli moved from town to town for decades, teaching mathematics at universities across Italy. Summa was a compilation of his life’s learnings. Published just half a century after the printing press was invented, it was the first printed book on abacco mathematics. It described, for the first time, many accounting tools we still use today, like double-entry book-keeping, balance sheets or ‘the rule of 72’. Instead of Latin, it was written in vernacular Italian, the language of the common people. All this made Summa a rage amongst Italy’s merchants. Copies of the book flew off the shelves.

Source: Flickr
Summa had an interesting brain-teaser, which can be distilled to this:
A and B play a ball game. They bet on the game — the first player to win six rounds of the game will win the entire prize pot. But the game gets interrupted mid-way, when A has won 5 games and B has won 3. How should they divide the stakes?
Pacioli attempted a solution to his ‘problem of points’: divide the stakes according to the number of rounds they had won: 5/8ths of the prize for A; 3/8ths for B. But this wasn’t a satisfying answer. After all, A was just one round away from getting the entire pot, while B hardly had a shot. Surely, A would consider the division unfair?
Ideally, they’d divide the stakes based on the likelihood of either person winning the whole game. But how would you measure that? In any one round, perhaps, both had an equal shot at winning. But what chance did B have of winning three straight rounds? Could one even put a number to it? This was a question of probability — one that society wasn’t advanced enough to answer. After all, this was before basic symbols like ‘+’, ‘-’ or ‘=’ existed. The word ‘probable’, back then, meant ‘praiseworthy.’
Before finding a solution, one needed a mathematical framework of the future. One soon came from a Milanese doctor, Girolamo Cardano. Cardano desperately needed such a framework — he was addicted to gambling. In his youth, he struggled to find work, and he spent the little money he earned to feed this addiction. These losses and disappointments drove him to seek a theory of chance itself.

Source: Wikipedia
Gamblers of the time had basic intuitions — they knew that if you threw a fair die, for instance, any of its sides could turn up. These intuitions, however, were not mathematical. Complex events made them falter. What would happen if one threw two dice at the same time? What were the chances that, say, a 6 would appear on at least one? Without mathematics, this couldn’t be answered.
Cardano created the mathematics they needed. He considered all possible results of a game as a ‘circuit’. If you knew the total size of the circuit and the number of results you wanted, you could calculate your chances of winning. For example, there were 36 ways of throwing two dice, and a 6 would appear in 11 of those. You thus had a 11/36 (~30.6%) chance of winning. Starting here, he worked his way through the basics of probability and how it could be measured — creating an entire body of knowledge to serve an addiction.
Cardano’s breakthroughs were published almost a century after his death, as Liber de Ludo Alea. This was more a gambling guide than a mathematical treatise. It even had a section on cheating. Still, it laid the foundations for our modern understanding of probability. In fact, Cardano defined the word ‘probability’ itself.
Cardano also attempted Pacioli’s problem of points. The answer, he realised, had to do with the number of rounds the players still had to win, not the number of rounds they’d already won. He devoted an entire chapter of another book of his, Practica Arithematica, to Pacioli’s error. Yet, his own solution — a 6:1 split — was wrong too. The real solution would come later, from the meeting of two extraordinary minds.
Two geniuses and a puzzle
The problem of points had reached the attention of another gambler in faraway France — the nobleman Chevalier de Méré. He, however, considered it unsolvable. In fact, he saw it as proof that mathematics could never explain the real world — something he would often tell his mathematician friends.
In one such discussion, de Méré introduced the problem to the young mathematician, Blaise Pascal. Pascal had a penchant for the unsolvable. He began his life as a child prodigy — his early work so precocious that scholars dismissed it as the work of his mathematician father. As a teenager, he invented the calculator to help his father with tedious calculations. When de Méré mentioned a problem that could never be solved, Pascal resolved to solve it.

Sources: World History Encyclopedia | Picryl
It was an audacious task. Pascal turned for help to another once-in-a-generation intellect, Pierre de Fermat. Fermat, fifteen years Pascal’s senior, was a lawyer that dabbled in mathematics as a hobby. For a hobbyist, however, he was extraordinarily gifted — making pioneering contributions to everything from coordinate geometry to calculus. A mere margin note of his created what would, for three and a half centuries, be the hardest problem in all of mathematics. Fermat was a friend of Pascal’s father, and Pascal reached out to him with de Méré’s problem.
Between July and October 1654, the two exchanged a series of letters, working through the problem of points. They bent and twisted it around, adding complications, looking for solutions that fit every variation. Fermat approached the problem from algebra, Pascal with intuitions he derived from geometry. Slowly, the answers came to them. Fermat came to a workable but cumbersome solution, counting all possible futures (like Cardano’s circuit) and identifying favourable cases. Pascal reduced this into a simple, elegant triangle:
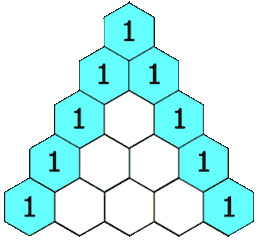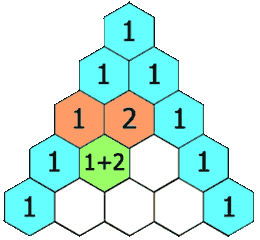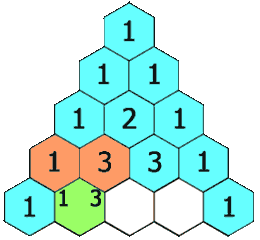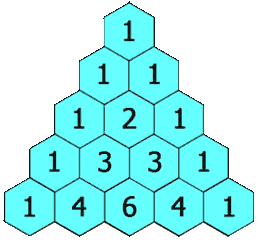
Source: Wikimedia
This was a system of beauty. It let one predict the outcomes of any arrangement of 50-50 events. It could predict the odds of a coin landing on heads six times in a row. Or the odds that, if you had three children, two would be daughters. Or that if you pulled five playing cards from a well-shuffled deck, at least three would be red. A simple, elegant triangle held all the answers you needed.
How would three rounds of Pacioli’s ballgame go? Look to the fourth row of the triangle. 1-3-3-1. There was a 1/8 possibility that a player would win all three rounds, and a 3/8 possibility that a player would win two of the three rounds. B could only win if she won three games in a row — a 1/8 shot. The stakes of their aborted game, therefore, should be divided in the ratio 7:1.
But solving the problem of points wasn’t just a matter of settling a gambling dispute. A satisfying solution would do more — it would help one think through the future in general. The problem required one to accommodate various interacting players, positioned differently, in complex and uncertain circumstances — all in a way that made sense mathematically. A ballgame was a simple laboratory to test such a system, but the system itself could help anyone working with uncertainty.
Fermat and Pascal hadn’t just solved a puzzle. They had created the mathematical backbone for forecasting.
The shopkeeper who counted London
A few years after the two Frenchmen’s leaps in probability, an English shopkeeper, John Graunt, made similar leaps in statistics. Through the day, Graunt sold ‘notions’ — buttons, clasps, and other small knick-knacks that keep one’s clothes together. He was also a self-taught scholar, however. Everyday, he woke up in the wee hours of the morning to study before he opened his shop.

Source: Picryl
One subject of his study was the ‘Bills of Mortality’ — weekly records of births and deaths in London. The City of London had long maintained these records to track deaths during the city’s many plague outbreaks. Once collected, though, the data merely sat there, with little purpose — until Graunt found one. He poured through them in his early morning study sessions, amusing himself with all the odd, unexpected things he saw in the numbers. But he also realised that they could serve a higher end.
This was before governments kept track of their population. This was fine when England was still an agrarian society. Back then, the number of individuals it had hardly mattered. Governments simply needed to look at the land under cultivation for collecting taxes or raising armies, and nothing else would justify the expense. But English society was changing quickly. Wealth was pouring in from its American colonies. Towns and cities were mushrooming around a new commercial class, which made money in new ways. The country needed a better way of administering people.
Graunt realised that the Bills of Mortality could, in his hands, become a guide to London’s people. It would tell him how many people there were in the city, and how they varied by sex, age, religion, health, occupation and more. This information had never existed before. It could change everything — from how traders conducted their business, to how governments looked after their people. He took half a century’s mortality data, reduced it into a few tables, and presented them with his own commentary, as the book Natural and Political Observations made upon the Bills Of Mortality.

Source: Wikimedia
Graunt’s work shaped people’s perceptions of the world they lived in. He was the first person, for instance, to estimate the population of London — as well as how it changed through migration. He made deductions about culture and society — such as, for instance, what murder rates in London and Paris (London’s being far lower) said about English and French societies. He had many insights around disease, how and when it spread, and who it affected the most. His work became enormously influential. Despite being a mere shopkeeper, he was soon inducted into the Royal Society, on the recommendation of King Charles II.
Graunt’s genius, however, wasn’t in compiling data, or even in his conclusions: it was in how he thought about data. He knew that the data he had was both incomplete and imperfect. After maintaining accounts for his shop for years, he saw how numbers in books failed to capture the complexity of the world. By itself, his data would only yield bland conclusions. If used blindly, they would be incorrect as well.
Graunt was cleverer than that. He reasoned his way through information, made guesstimates, and found global inferences in samples of data. He had a series of blinding insights: around sampling, assumptions, statistical models, averages, ‘normalcy’, pollution and distortions in data, and more. With these, he single-handedly created a toolkit that statisticians have used ever since. This turned the collection of data — a cumbersome, largely pointless exercise — into a powerful way of understanding the world.
For modern finance to emerge, however, we needed one final step: combining Graunt’s statistical methods with probability. That would take a long process. But it was put into motion soon, by an astronomer looking for variety.
The starman bets on death
Thirty years after Graunt published his findings, one of England’s premier astronomers, Sir Edmund Halley, used them to create a basic framework for risk management — the first time anyone had attempted such a thing.
Halley had a reputation for genius from an early age. As a young man, he dropped out of Oxford University to go to a remote volcanic island in the Southern Hemisphere. There, he observed the southern skies, preparing star charts that made him a celebrity in astronomy circles before his twentieth birthday. Much of Halley’s work — like Graunt’s — involved poring over large tables of data and looking for patterns. It was through this sort of number-crunching, for instance, that he discovered the orbit of the famous comet named after him.
Halley was also a colourful man, with many curiosities. He was vivacious and energetic. He drank, he smoked, he swore, all of it heavily. He helped Sir Isaac Newton work through the law of gravity, and funded the publication of his masterpiece, Principia Mathematica. He briefly tried to salvage gold from a Spanish shipwreck, and for that, he devised the world’s first deep sea diving suit. He also experimented with opium, writing about how it gave him tremendous clarity.

Source: World History Encyclopedia
Graunt’s demographic work was one such curiosity of Halley’s. He had promised the Royal Society a paper, and was looking for something fun to write about. And so, he tried his hand at the same sort of analysis as Graunt. He’d been sent five years’ worth of raw data on births and deaths from Breslaw (today’s Wrocław), and he began using it to estimate the city’s population. Breslaw was easier to study than London — it was small, quiet, and it didn’t draw too many migrants. That made it relatively easier for him to get to his answer: Breslaw had about 34,000 people.
But then, he tried something different. By looking at the ages at which people seemed to die, he worked out the life expectancy of its residents. With that, he realised, you could make a new kind of bet: if the average Breslawian could expect to live till age 57, you knew the chances that someone aged 30, for instance, would live another year. This information would be invaluable to an insurance company! This would let them price their annuities exactly right. Halley built out neat tables that insurance companies could use to calculate annuities — inventing the actuarial life table that insurers use today.
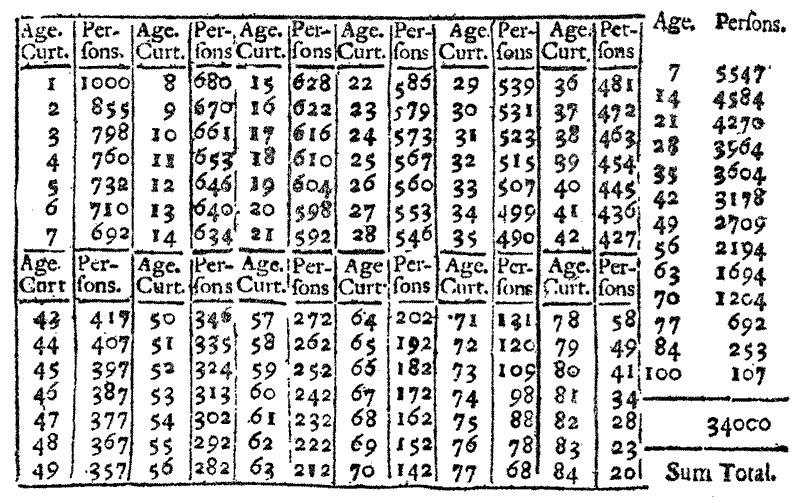
Source: IUSSP
It would take another century for the insurance industry to adapt to Halley’s system. Still, Halley made two major breakthroughs. One, he found a major commercial application for ideas that had, thus far, been side-projects for hobbyists. Two, he combined statistics and probability. If you had enough data and learnt how to interpret it, he realised, you could fine-tune the risk you took while betting on the future. This idea, perhaps, is the beating heart of modern finance.
The dawn of modernity
By now, the Enlightenment was well underway.
European sailors were learning to take audacious risks. They went on grand voyages across the world: to India, to China, to South-East Asia. They’d sail for months through rough seas, sneaking past the fleets of rival merchants and suspicious foreigners, to reach empires which could, if annoyed, swat them away like flies. Much could go wrong. But at the other end were spice, cloth, sugar, tea, and other exotic delights — all of which could make them immensely wealthy.
The last five hundred years had taught them that risk wasn’t to be avoided — it was to be managed. Entrepreneurs were creating techniques to do just that. Merchants pooled their resources to form joint stock companies. The Dutch East India Company, in 1602, became the first company to sell its shares to the public. Within a hundred years, brokers that frequented Edward Lloyd’s coffee shop in London would lay the foundations of insurance underwriting. For the first time, people were learning to spread risk and hedge their bets systematically.

Source: Lloyd’s
These bets paid off. In a few generations, Europe’s merchants practically ruled the world. Their actions did, of course, cause the suffering of millions. But those they dominated, India included, have embraced their innovations in risk-management. The Enlightenment-era risk management vehicles remain at the heart of modern finance. Securities help people break risk into small parcels. Bankers and insurers patch together many parcels of risk to make it predictable. Fundamentally, these are just better bets, based on statistics and probability.
We come across the same ideas wherever else we work with uncertainty: from formulating IPL strategies, to building rockets, to setting up government programs. Across domains, they help us make better decisions. Perhaps all the wonders of the modern world, at their heart, all come from this mass of better decisions.
In that sense, maths made the modern world.
Post-script: Why you should read Against the Gods
These stories aren’t mine. They come from a mere fifty pages of Peter Bernstein’s Against the Gods. They’re his prelude, really, to the real story: about the many innovations of the next three hundred years, which have shaped today’s financial industry.
I have never liked maths, perhaps because it felt like a list of procedures one had to memorise to survive an exam paper. Bernsteins’ book, however, is a history. He reminds you that we didn’t receive maths as some sort of divine textbook, pre-made and ready-to-use — we created it, layer-by-layer. Each soporific textbook chapter, the book reminds you, began as a brilliant flash of insight in someone’s mind. He breathes life into what, to me, was always an abstract, faraway subject.
If you like these stories, Bernstein has more. So far, we’ve seen how people had developed an inkling that they could, with some clever math, peer into the future. With time, though, they would explore this newfound ability in depth. That is the story which drives the rest of his book. We see probability and statistics grow in sophistication, improving people’s ability to interpret data and make better decisions. Generations of economists — from Keynes, to von Neumann, to Kahneman and Tversky — use these ideas to examine the relationships between people and their money. All of this steadily informs the finance industry, creating many of the models we work with — like Portfolio Theory, Prospect Theory, or the Random Walk Hypothesis.
Alongside, though, Bernstein also introduces you to more of the fascinating characters that drove these innovations. Here are just a few: the Bernoullis, a large family of rude, quarrelsome, genius aristocrats; Gauss, a brilliant recluse whose hometown was spared by Napoleon because he considered him “the greatest mathematician of all time”; Galton: a social snob that was clinically obsessed with counting things. There are many more. Bernstein is deeply interested in the people behind the theory, and his descriptions enliven what could easily have been a tedious textbook.
We might come back to some of his stories on this blog, some time. Until then, though: do read the book.


Wow, this was such a fascinating read! It’s amazing how ideas like probability, statistics, and averages evolved over centuries to shape modern finance and even our daily decision-making. It really shows how deeply maths connects with real-world thinking.
I’ve always been curious about how these mathematical concepts work in simple, everyday tools too. For example, I recently came across an average calculator
that helps visualize how averages and data balancing actually works.It really puts theory into practice in a fun way.
Thanks for sharing this .It definitely made me appreciate the human side of mathematics a lot more!
Excellent!
Lucid and in depth.
Long Journey turned into exciting and catching story.
”A satisfying solution would do more — it would help one think through the future in general.”
Is this a mere line or important Management Principle! An example, there are numerous hidden, great.
Thanks Sangram!
That’s not just a management principle, it’s a mathematical principle. It is key to large parts of management studies. 🙂
A brief history of modern finance. A lucid article indeed. Will be waiting for more.
Thanks Dodul! Do subscribe to the blog for more such stuff!
Our astrology, Jyotish Shastra, panchang is all pure mathematics.
It’s certainly true that a lot of early maths was created to compute the movement of celestial objects through the skies. 🙂
Excellent article. Kept me engrossed till the end. Eagerly waiting for more such posts.
Thanks, Ninad! We’ll keep sending new posts your way – do subscribe to the blog!
Wow, the blog is amazing. You have good writting skills. I couldn’t stop until it’s finished.
Zerodha has something extra compared to other brokers and this blog is one more example.
Thanks for writing this, loved it. Waiting for more.
Thanks.
You made our day, Changdeo! Thanks for the kind words. 🙂
Hi bro please write only stories which can reduce the Pain of BSE n NSE,,,
Eagerly waiting to read your stories which can make our Portfolio look gorgeous 🥰
i guess every Trader must want to learn from your side the magic….The Magic to convert the damn Red into GREEN 💚
From:-
A 5 days old New Born Baby at Zerodha
Keep Wishing 🤞👍
Alas, Surinder, we’re just nerds that like obsessing over anything to do with the markets. Subtext is our attempt to give voice to these passions.
If you’re interested in something that can help your trading directly, can we recommend Varsity? It’ll help you equip yourself with the skills and attitude you need as a trader. Do also check out our new Markets podcast – our attempt to decode the news for the trading community!