9.1 – लीनियर रिग्रेसन (Linear Regression) – एक परिचय

पिछले अध्याय में स्ट्रेट लाइन इक्वेशन (Straight Line Equation) को समझाया गया था। हमने बहुत सरल उदाहरण का इस्तेमाल करके ये समझाने की कोशिश की थी कि दो वेरिएबल के बीच के संबंधों कैसे पता किया जा सकता है। उदाहरण इतने सीधे थे कि आप उसे देख कर भी जान सकते थे कि उनके बीच में कैसा संबंध है। अध्याय के अंत में दो वेरिएबल का एक टेबल दिखाया था और ये सवाल उठाया था कि इनमें संबंध कैसे स्थापित करें? यहां पर हम कैसे स्लोप और इंटरसेप्ट यानी E की वैल्यू कैसे निकालें? 

इस अध्याय में हम इसी संबंध को स्थापित करने का तरीका ढूंढेंगे और रिलेटिव वैल्यू ट्रेडिंग तकनीक की तरफ बढ़ेंगे। सबकी सुविधा के लिए मैं उस टेबल को फिर से डाल रहा हूं –

X	Y
10	3
12	6
8	4
9	17
20	36
18	22

 

सीधे तौर पर देखने से इनके बीच में कोई संबंध पता नहीं चलता है।

ऐसी स्थिति में हम लीनियर रिग्रेसन (Linear Regression) तकनीक का इस्तेमाल करते हैं। इस सांख्यिकी तकनीक में इनपुट के तौर पर संख्याओं के दो समूह को डाला जाता है, और आउटपुट के तौर पर हमें बहुत सारी सूचनाएं मिलती हैं जिनमें इंटरसेप्ट और अचर (Constant) संख्या भी होती है जिससे हम स्ट्रेट लाइन इक्वेशन (Straight Line Equation) बना सकते हैं।

लीनियर रिग्रेसन (Linear Regression) निकालने के लिए हम एक्सेल का उपयोग कर सकते हैं। संख्याओं के दो समूह का लीनियर रिग्रेसन (Linear Regression) को एक्सेल पर निकालने का तरीका नीचे बताया जा रहा है।

कदम 1 – प्लग इन इन्स्टॉल  करें – Install the Plugin

एक नया एक्सेल शीट खोलें और उसमें X  और Y की वैल्यू डालें जैसा कि ऊपर के टेबल में दिखाया गया है। जैसे कि मैंने नीचे दिखाया है – 

ये हमारा डेटा है। याद रखें कि Y एक डिपेंडेंट वेरिएबल बन जाता है जिसकी वैल्यू इंडिपेंडेंट वेरिएबल X पर निर्भर करती है। X  और Y दोनों को लीनियर रिग्रेसन के इनपुट के तौर इस्तेमाल किया जाएगा।

एक्सेल शीट में डेटा रिबन (लाल रंग के घेरे से दिखाए गए) पर क्लिक करें, जैसा कि चित्र में दिख रहा है –

डेटा रिबन अब आपको डेटा एनालिसिस का ऑप्शन देगा। इसे नीले रंग से हाईलाइट किया गया है। हो सकता है कि आपमें से कुछ लोगों को ये ऑप्शन ना दिखाई दे। अगर ऐसा है तो घबराने की जरूरत नहीं है, आपको सिर्फ ये करना है – 

फाइल पर क्लिक करें

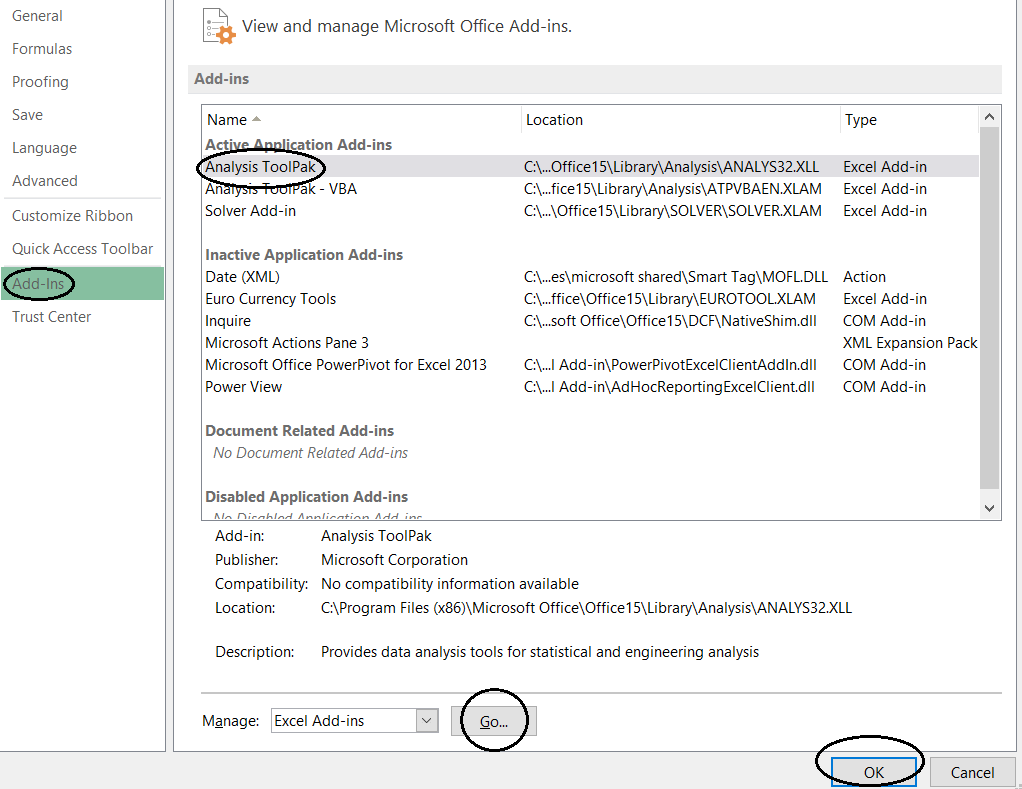
इसके बाद एक नई विन्डो खुलेगी और उसमें बायीं तरफ के पैनल में आपको ये ऑप्शन दिख जाएगा

इस ऑप्शन पर क्लिक करने पर आपको बहुत सारे विकल्प मिलेंगे,। इसमें से आपको बायीं तरफ के पैनल में ऐड इन (Add Ins) पर क्लिक करना है और फिर गो (Go) का बटन दबाना है और फिर अंत में ओके (OK) पर क्लिक करना है।इस तरह से आप डेटा रिबन (Data Ribbon) में डेटा एनालिसिस (data Analysis) को जोड़ पाएंगे।

अब आप एक्सेल शीट बंद करके अपने कम्प्यूटर को दोबारा चालू कर लें। अब आपकी तैयारी पूरी हैं।

कदम 2 – वैल्यू भरिए- Enter the Values

अब आपके एक्सेल शीट में डेटा एनालिसिस का पैक है। अब आपको डेटा एनालिसिस पैक में लीनियर रिग्रेसन फंक्शन का इस्तेमाल करना है। इसके लिए डेटा रिबन पर क्लिक करें, और डेटा एनालिसिस को सेलेक्ट करें। इसकेबाद एक पॉप अप खुलेगा जिसमें आपको बहुत सारे ऑपरेशन की लिस्ट दिखेगी जिनको आप डेटा सेट में इस्तेमाल कर सकते हैं। आपको उसमें से रिग्रेसन को चुनना है।

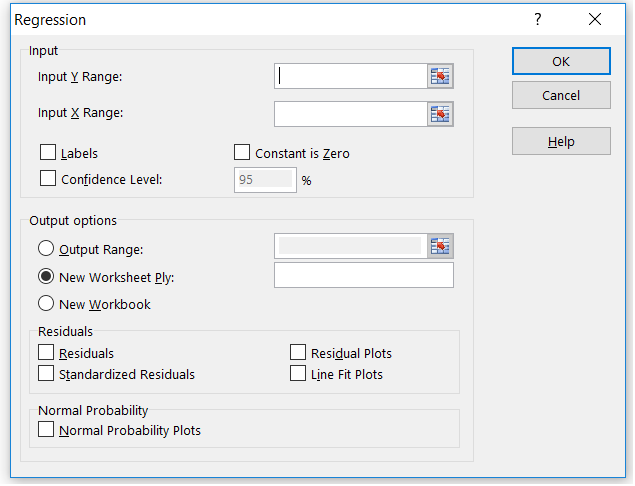
रिग्रेसन को सेलेक्ट कर के ओके (OK) दबाने पर आपको ये पॉप अप (Pop Up) दिखेगा।

जैसा कि आप देख सकते हैं कि यहां पर बहुत सारे फील्ड हैं। आपको पहले सेक्शन पर ध्यान देना है, जो कि इनपुट का सेक्शन है। इसमें दो फील्ड हैं – इनपुट X रेंज और इनपुट Y रेंज। आप समझ ही गए होंगे कि Y डिपेंडेंट वेरिएबल के लिए है और X इंडिपेंडेंट वेरिएबल के लिए।

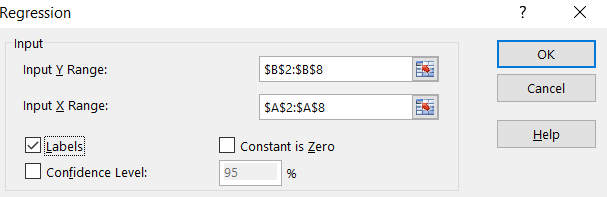
यहीं पर हमें X और Y सीरीज के डेटा को भरना है। इसके लिए इनपुट चैनल पर क्लिक करें और X रेंज और Y रेंज को सेलेक्ट करें।

यहां पर ध्यान दीजिए कि मैंने लेबल बॉक्स को टिक किया है ,ये बताता है कि पहले सेल (Cell) की  वैल्यू यानी A2 और B2 में सीरीज की वैल्यू है यानी X और Y है।

मेरी सलाह है कि आप बाकी इनपुट पर ध्यान ना दें।

आउटपुट की तरफ में आपको इसे ज़रूर चुनें- 

न्यू वर्कशीट (new worksheet) को सेलेक्ट करने से आपका आउटपुट डेटा एक नई वर्कशीट में मिलेगा। मैंने यहां पर रेजिडुअल्स (Residuals) और स्टैन्डर्डाइज्ड रेजिडुअल्स (Standardised Residuals) पर भी टिक किया है। ये क्या हैं इस पर हम बाद में चर्चा करेंगे अभी के लिए बस आप इनको सेलेक्ट कर लें।

अब आप लीनियर रिग्रेसन ऑपरेशन करने के लिए तैयार हैं। सबसे ऊपर दायीं तरफ ओके (OK) बटन पर क्लिक करें।

एक्सेल अब इन इनपुट को लेगा और लीनियर रिग्रेसन ऑपरेशन करेगा। इसका परिणाम उसी वर्कबुक में एक नई शीट में मिल जाएगा।

9.2 – लीनियर रिग्रेसन आउटपुट

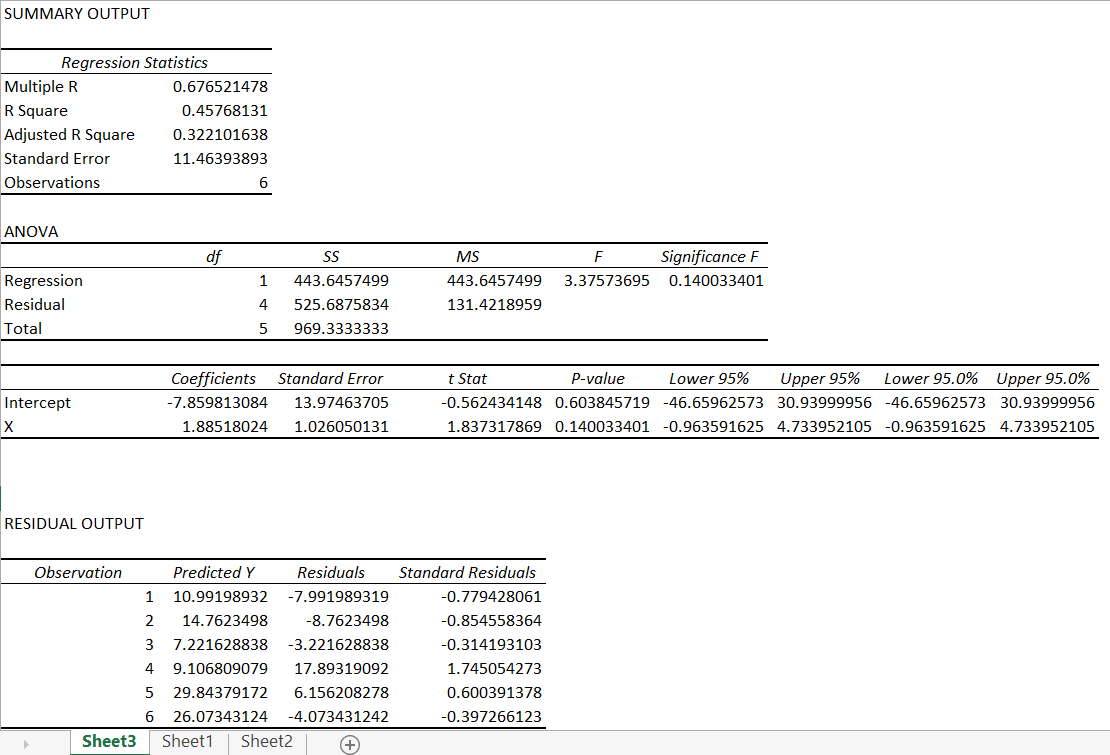
लीनियर रिग्रेसन का आउटपुट ऐसा दिखेगा, इस आउटपुट का सारांश (Summary) एक नई शीट में होगा।

मुझे पता है कि इसे देख कर आप डर सकते हैं। इसमें काफी सूचनएं हैं। हम आगे जाते हुए इसको छोटे छोटे टुकड़ों में समझते रहेंगे।

लेकिन अभी, स्लोप और इंटरसेप्ट को तलाशते हैं। मैंने नीचे के चित्र में इनको हाईलाइट किया है –

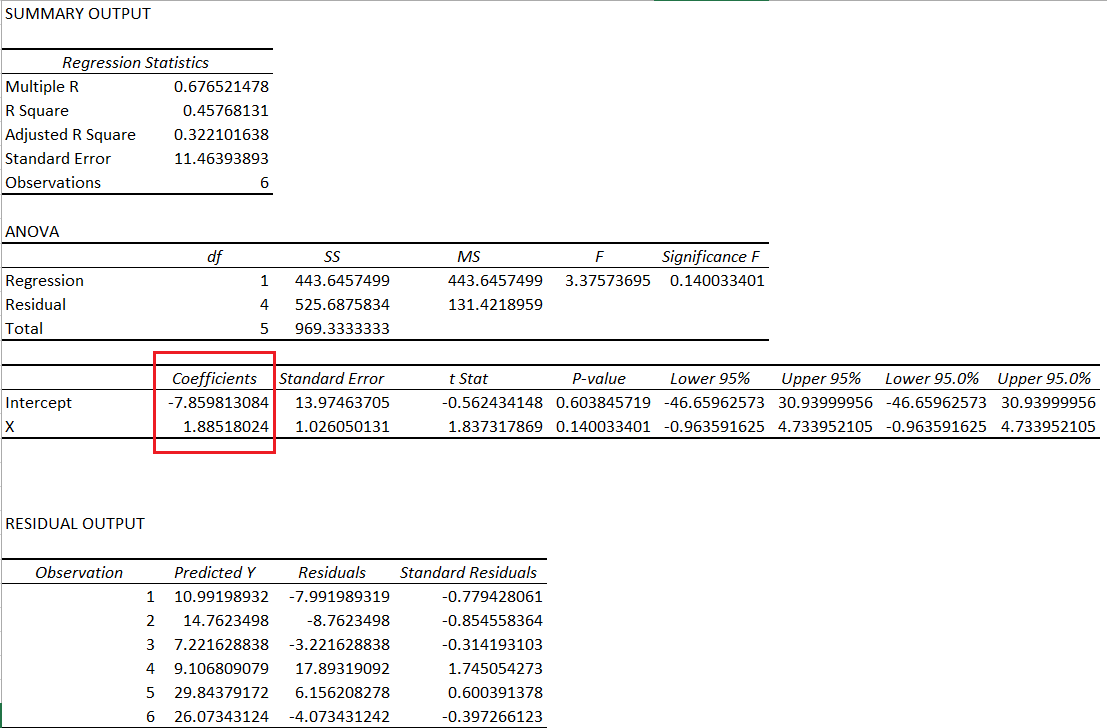
लाल रंग से हाईलाइट किए कोएफिसिएंट (Coefficients)  ही इंटरसेप्ट (अचर) और स्लोप (X) हैं।

यहां पर स्लोप को X से दिखाया गया है और वो भ्रम पैदा कर सकता है लेकिन आप उससे किसी भ्रम में ना पड़ें। अगर यहां पर X की जगह M होता तो वो स्ट्रेट लाइन इक्वेशन के हिसाब से ठीक होता लेकिन हमें X से ही काम चलाना पड़ेगा।

तो,

• समीकरण का स्लोप = 1.885
• इंटरसेप्ट (अचर-Constant) = 7.859813

इसके आधार पर, हमारे डेटा का स्ट्रेट लाइन इक्वेशन होगा –

y = 1.885*x + (-7.859813) या

y = 1.885*x – 7.859813

तो इसका मतलब क्या हुआ?

आपको याद होगा कि पिछले अध्याय में हमने कहा था कि ये समीकरण हमें  X के आधार पर Y की यानी डिपेंडेंट वेरिएबल की वैल्यू पता करने में मदद करता है। एक बार फिर से अपने टेबल पर नजर डालते हैं –

 

X	Y
10	3
12	6
8	4
9	17
20	36
18	22
15	??

 

मैंने यहां पर X की एक नई वैल्यू 15 डाली है, अब स्लोप और इंटरसेप्ट का उपयोग करके हम Y की वैल्यू पता कर सकते हैं। 

 Y = 1.885 * 15 – 7.859813

= 28.275 – 7.859813

= 20.415

तो अब अगर X की वैल्यू 15 है तो फिर Y की वैल्यू 20.415 होगी।

आप के दिमाग में सवाल आ सकता है कि ये कितनी सही वैल्यू है।

तो याद रखिए ये सिर्फ एक अनुमान है इसलिए इसको एकदम सही ना मान लें। उदाहरण के तौर पर मान लीजिए कि X की वैल्यू 18 है, तो स्ट्रेट लाइन इक्वेशन के हिसाब से Y की वैल्यू होगी –

y = 1.885*18 – 7.859813

= 33.93 – 7.859813

= 26.07019

लेकिन में इसकी वास्तविक वैल्यू 22 दी गयी है।

इसका मतलब है कि Y की दो वैल्यू होगी –

1. स्ट्रेट लाइन इक्वेशन के हिसाब से Y की अनुमानित वैल्यू
2. Y की वास्तविक वैल्यू

इन दोनों वैल्यू के बीच के अंतर को रेजिडुअल्स (Residuals) कहते हैं। उदाहरण के लिए जब X की वैल्यू 18 है तो Y की रेजिडुअल्स वैल्यू (Y की वास्तविक वैल्यू और अनुमानित वैल्यू का अंतर) होगी –

26.07019 – 22

= 4.070187

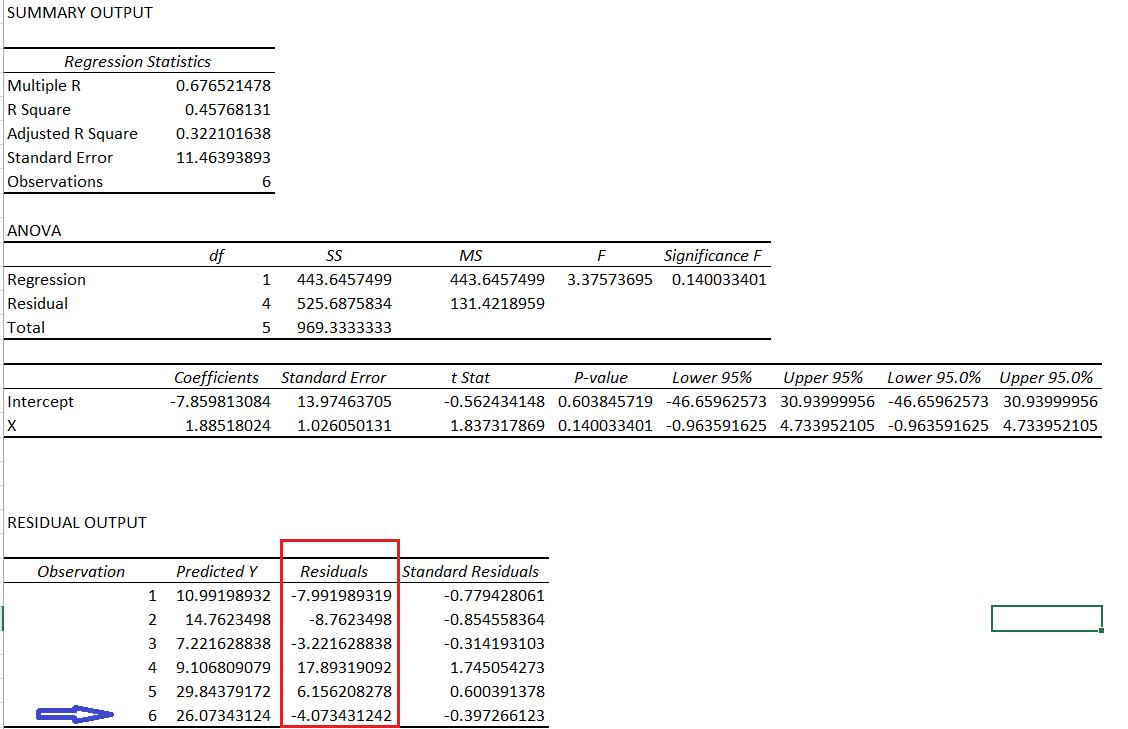
जब आप लीनियर रिग्रेसन निकालते हैं तो उसके आउटपुट में भी आपको रेजिडुअल्स (Residuals) मिलता है। इसको मैंने नीचे हाईलाइट किया है – 

जब X की वैल्यू 18 है तो Y की रेजिडुअल्स वैल्यू क्या होगी उसको भी मैंने हाईलाइट किया है।

आपको बता दूं कि रिलेटिव वैल्यू ट्रेडिंग (RVT) में रेजिडुअल्स की काफी बड़ी भूमिका होती है।

आप एक्सेल शीट को यहां से डाउनलोड कर सकते हैं।here.

इस अध्याय की मुख्य बातें 

• लीनियर रिग्रेसन एक सांख्यिकीय ऑपरेशन है जो स्ट्रेट लाइन इक्वेशन बनाने में मदद करता है।
• लीनियर रिग्रेसन को निकालने के लिए एक्सेल का इस्तेमाल किया जा सकता है। इसके लिए एक्सेल के एक प्लग इन को इन्स्टॉल करना पड़ता है। 
• लीनियर रिग्रेसन से हमें बहुत सारे आउटपुट मिलते हैं जिसमें स्लोप और इंटरसेप्ट भी होते हैं। 
• स्लोप और इंटरसेप्ट का उपयोग करके हम Y की वैल्यू पता कर सकते हैं। 
• Y की वास्तविक वैल्यू और अनुमानित वैल्यू का अंतर को रेजिडुअल्स (Residuals) कहते हैं।
• आउटपुट सारांश (Summary) में भी आपको रेजिडुअल्स (Residuals) की वैल्यू मिलती है।