5.1 – नॉर्मल डिस्ट्रीब्यूशन – एक बार फिर 

आपने ऑप्शन के मॉड्यूल में नॉर्मल डिस्ट्रीब्यूशन के बारे में पढ़ा होगा। अगर आपने नहीं पढ़ा है तो मेरी सलाह यह होगी कि आप पहले जाकर नॉर्मल डिस्ट्रीब्यूशन का अध्याय पढ़ लें। 

यह एक बहुत ही महत्वपूर्ण विषय है और इस अध्याय में आगे बढ़ने के पहले उस अध्याय को पढ़ना आपके लिए अच्छा होगा। नॉर्मल डिस्ट्रीब्यूशन का सिद्धांत पेयर ट्रेडिंग की उन दोनों तकनीक में काम आने वाला है जिन पर हम चर्चा करने वाले है- मार्क विसलर की पेयर ट्रेडिंग तकनीक और दूसरी तकनीक जिस पर हम मॉड्यूल में आगे चर्चा करेंगे। 

मैं एक बार संक्षेप में नॉर्मल डिस्ट्रीब्यूशन के सिद्धांत को दोहरा दे रहा हूं जिससे आपकी याद ताजा हो जाए। 

नॉर्मल डिस्ट्रीब्यूशन का सामान्य सिद्धांत जिसे आपको जानना चाहिए –

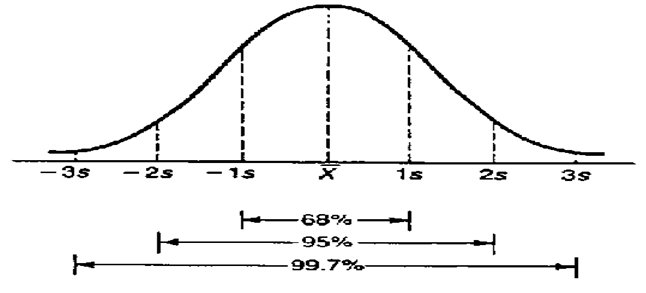
• 1st स्टैंडर्ड डेविएशन के भीतर आप 68% डेटा को देख सकते हैं 
• 2nd स्टैंडर्ड डेविएशन में आप 95% डेटा को देख सकते हैं 
• 3rd स्टैंडर्ड डेविएशन के भीतर आप 99.7% डेटा पर नजर डाल सकते हैं 

इन बिंदुओं को आप नीचे के चित्र के रूप में भी देख सकते हैं 

वैसे आपकी जानकारी के लिए मैं बता दूं कि डेटा और कई तरीके से डिस्ट्रीब्यूट होता है, जैसे यूनिफॉर्म डिस्ट्रीब्यूशन, बायनॉमियल डिस्ट्रीब्यूशन, एक्स्पोनेंशियल डिस्ट्रीब्यूशन आदि। 

5.2 – सांख्यिकीय विस्तार 

पिछले अध्याय में हमने सांख्यिकी से जुड़े हुए तीन मानकों की चर्चा की थी – मीन, मीडियन और मोड। अब हम इन तीनों को पेयर डेटा के लिए कैलकुलेट करेंगे, मतलब डिफरेंशियल, स्प्रेड और रेश्यो के लिए मीन, मीडियन और मोड निकालेंगे। हम यह काम एक्सेल शीट के जरिए करेंगे। 

मैंने पिछले अध्याय में जिस एक्सेल शीट पर काम किया था, मैं उसी पर काम करना जारी रखूंगा। आप चाहें तो इस एक्सेल शीट को अध्याय के अंत में दिए गए लिंक के जरिए डाउनलोड कर सकते हैं। 

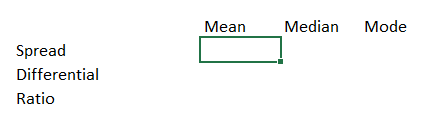
इस शीट को इस तरह से सेट-अप किया गया है

एक्सल फंक्शन ये हैं

1. मीन  – ‘=average()’
2. मीडियन – ‘=median()’
3. मोड – ‘=mode.mult()’

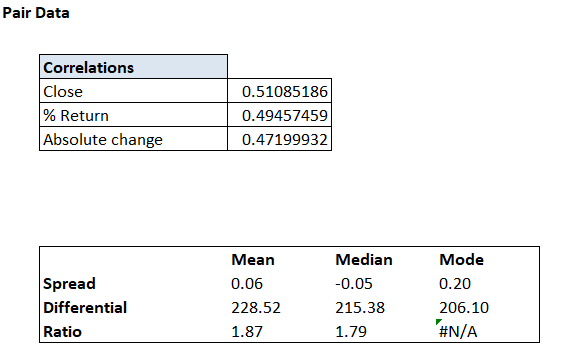
संख्याएं नीचे दी गई हैं –

जैसा कि आप देख सकते हैं कि कोरिलेशन की संख्याएं पिछले अध्याय में ही कैलकुलेट कर ली गई थीं। 

अब हमारा डेटा सेट अप तैयार है, अब हमें यहां पर सिर्फ एक वेरिएबल जोड़ना है जो है – स्टैंडर्ड डेविएशन। आपको स्टैंडर्ड डेविएशन का सिद्धांत पहले समझाया जा चुका है। मेरी सलाह है कि आप इस अध्याय ( read this chapter) को पढ़ लें। यहां मैं उसको संक्षेप में बता देता हूं –

स्टैंडर्ड डेविएशन औसत से होने वाली दूरी या बदलाव यानी डेविएशन को दिखाता है। स्टैंडर्ड डेविएशन की किताबों में दी गई परिभाषा है – “सांख्यिकी में स्टैंडर्ड डेविएशन (SD ग्रीक शब्द सिग्मा σ) एक माप है जो बताता है कि किसी दिए गए डेटा में कितना बदलाव या वेरिएशन या डिस्पर्शन हुआ है।“ 

तो एक तरह से स्टैंडर्ड डेविएशन हमें बताता है कि डेटा में बदलाव कितना हो रहा है यानी उसकी वैरिएबिलिटी कितनी है, जिससे हमें यह पता चलता है कि डेटा कहां तक फैला है। अब मैं इसको अपने पेयर के डेटा के संदर्भ में समझाने की कोशिश करता हूं।

थोड़ी देर पहले हमने डिफरेंशियल का जो डेटा निकाला है वो ये है- 

कुल मिला कर, हमारे पास 496 डिफरेंशियल डेटा प्वाइंट हैं। हमने थोड़ी देर पहले इस अध्याय में इनका औसत निकाला था जो कि 228.52 है। 

अब अगर मैं आपसे पूछूं कि डेटा प्वाइंट में औसत से कितना बदलाव दिख रहा है यानी इसकी वैरिएबिलिटी कितनी है? या अगर एक दूसरे तरीके से पूछें कि मुझे यह क्यों जानना है कि इस डेटा में औसत से कितनी दूरी तक का बदलाव दिख रहा है यानी इसकी वैरिएबिलिटी कितनी है? 

वास्तव में, अगर हमें यह नहीं पता हो कि हमारा डेटा औसत से कितनी दूर तक इधर-उधर जा सकता है, तो हमारे लिए यह उस डेटा के व्यवहार का आकलन करना मुश्किल होगा। उदाहरण के तौर पर जब हमारे पास 498वें नंबर का डेटा प्वाइंट आएगा तो हम यह देख पाएंगे कि यह डेटा मीन के आसपास या किसी एक दायरे में है या नहीं। 

वास्तव में, ये पेयर ट्रेडिंग की सबसे जरूरी चीज है। 

इस बदलाव को मापने का तरीका है स्टैंडर्ड डेविएशन। 

व्यक्तिगत तौर पर मुझे लगता है कि स्टैंडर्ड डेविएशन से इसे आसानी से नापा जा सकता है, लेकिन बहुत सारे ट्रेडर ऐसे हैं जो एक दूसरा तरीका अपनाते हैं जिसे एब्सॉल्यूट डेविएशन (Absolute Deviation )कहा जाता है। स्टैंडर्ड डेविएशन और एब्सॉल्यूट डेविएशन, दोनों हमें डेटा में आ सकने वाले बदलावों को बताते हैं। लेकिन इन दोनों में डेटा को अलग अलग तरीके से देखा जाता है।

मैं आपको स्टैंडर्ड डेविएशन और एब्सॉल्यूट डेविएशन के बीच का अंतर समझाने का तरीका खोज रहा था तब मुझे इन्वेस्टोपीडिया पर एक व्याख्या मिली जो कि मुझे काफी अच्छी लगी, इसलिए मैं उसको ही यहां पर दे रहा हूं – 

किसी भी डेटा समूह में हो सकने वाले बदलाव को नापने के कई तरीके हो सकते हैं, लेकिन दो सबसे लोकप्रिय तरीके हैं- स्टैंडर्ड डेविएशन और औसत यानी एवरेज डेविएशन। ये दोनों काफी मिलते-जुलते हैं लेकिन इनको कैलकुलेट या इनकी गणना करने का तरीका और उनसे निष्कर्ष निकालने का तरीके में कुछ अंतर है। रेंज यानी दायरा निकालना और वोलैटिलिटी निकालना फाइनेंस की दुनिया में काफी महत्वपूर्ण माना जाता है, इसीलिए अकाउंटिंग, इन्वेस्टिंग और इकनॉमिक्स से जुड़े हुए लोगों को इन दोनों को अच्छे से समझना होता है।

स्टैंडर्ड डेविएशन, डेटा में हो सकने वाले बदलाव यानी वैरिएबिल्टी को नापने का सबसे आम तरीका है। स्टॉक मार्केट और दूसरे निवेश में वोलैटिलिटी को नापने के लिए अक्सर इसका इस्तेमाल होता है। स्टैंडर्ड डेविएशन को निकालने या कैलकुलेट करने के लिए सबसे पहले वैरियंस को पता करना होता है। इसके लिए आपको हर डेटा प्वाइंट से मीन को घटाना होता है, फिर उसका वर्ग निकालना होता है, इन को आपस में जोड़ना होता है और फिर इन सब का औसत निकालना होता है। वैसे वैरियंस अपने आप में वैरिएबिलिटी निकालने और रेंज यानी दायरा निकालने का एक अच्छा तरीका होता है। वैरियंस जितना ज्यादा होता है डेटा का स्प्रेड उतना ही ज्यादा होता है। स्टैंडर्ड डेविएशन वास्तव में कुछ और नहीं बस वैरियेंस का वर्गमूल होता है। हर डेटा प्वाइंट और मीन के बीच के अंतर का वर्ग निकालना इसलिए अच्छा होता है क्योंकि इससे मीन के नीचे के डेटा प्वाइंट से आने वाले नेगेटिव डिफरेंस से बचा जा सकता है। लेकिन इसका यह भी मतलब होता है कि वैरियंस की यूनिट वास्तविक डेटा की यूनिट से अलग हो जाती है। इसीलिए वैरियंस का वर्गमूल निकाला जाता है ताकि स्टैंडर्ड डेविएशन वापस वास्तविक यूनिट में आ सके और उसका इस्तेमाल और निष्कर्ष निकालना आसान हो।

बदलाव यानी वैरिएबिल्टी को नापने का दूसरा तरीका है एवरेज डेविएशन जिसे एब्सॉल्यूट डेविएशन (Absolute Deviation) भी कहा जाता है। एवरेज डेविएशन निकालने के लिए वास्तविक डेटा को वैसे ही इस्तेमाल किया जाता है। डेटा और मीन के बीच निगेटिव डिफरेंस की समस्या से बचने के लिए संख्याओं का वर्ग यहां नहीं निकाला जाता। एवरेज डेविएशन निकालने के लिए डेटा के हर प्वाइंट से मीन को घटाते हैं, उसके बाद उन सब को जोड़ते हैं, फिर इसका औसत निकालते हैं। इस तरीके में, मीन एब्सॉल्यूट वैल्यू का इस्तेमाल कम होता है क्योंकि एब्सॉल्यूट वैल्यू लेने पर आगे की गणना या कैलकुलेशन, स्टैंडर्ड डेविएशन के मुकाबले ज्यादा बड़ी और मुश्किल हो जाती है। 

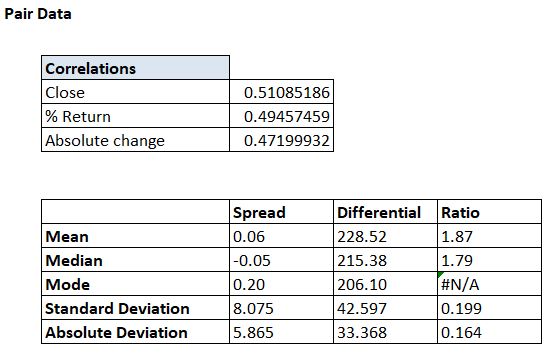
अब हम पेयर डाटा के तीनों अवयवों- मीन, मीडियन और मोड के लिए स्टैंडर्ड डेविएशन और एब्सॉल्यूट डेविएशन ((Absolute Deviation)) निकालेंगे। 

मैंने यहां पर बदलाव किया है- Y-Axis मीन, मीडियन और मोड के लिए और X-Axis को डिफरेंशियल रेश्यो और स्प्रेड के लिए रखा है। इस वजह से ऊपर के चित्र और नीचे के चित्र में थोड़ा सा अंतर होगा।

इन वैरिएबल को निकालने के एक्सेल फंक्शन हैं

स्टैंडर्ड डेविएशन – ‘=Stdev.p()’

एब्सॉल्यूट डेविएशन – ‘=avedev()’

एक बात और – मीन, मीडियन, मोड, स्टैंडर्ड डेविएशन और एब्सॉल्यूट डेविएशन को बेसिक डिस्क्रिप्टिव स्टैटिसटिक्स (Basic Descriptive Statistics) भी कहा जाता है।

5.3 – स्टैंडर्ड डेविएशन टेबल

जैसा कि आपको पता है कि स्टैंडर्ड डेविएशन हमें यह बताता है कि डेटा में कितना वैरिएशन या बदलाव हो रहा है। अब हम थोड़ा आगे बढ़ते हैं और इस वैरिएशन या बदलाव को नापने की कोशिश करते हैं। ऐसा करने से हमें पता चलेगा कि मीन की संख्या से कितना वैरिएशन या बदलाव देखने को मिल रहा है। उदाहरण के तौर पर 498वां डिफरेंशियल डेटा 275 हो सकता है।  वैरिएशन को नाप कर हम यह पता कर सकते हैं कि 275 मीन से ऊपर है या मीन से बहुत ज्यादा नीचे है। 

इस सूचना के आधार पर हम फैसला कर सकते हैं कि हमें पेयर को खरीदना है या हमें पेयर को शॉर्ट करना है। वैसे, इस बारे में आगे फिर चर्चा करेंगे। लेकिन अभी हम वैरिएशन या बदलाव को नापने की कोशिश करते हैं। ऐसा करने के लिए, हमें पहले एक टेबल बनाना होगा जिसे स्टैंडर्ड डेविएशन टेबल कहते हैं। 

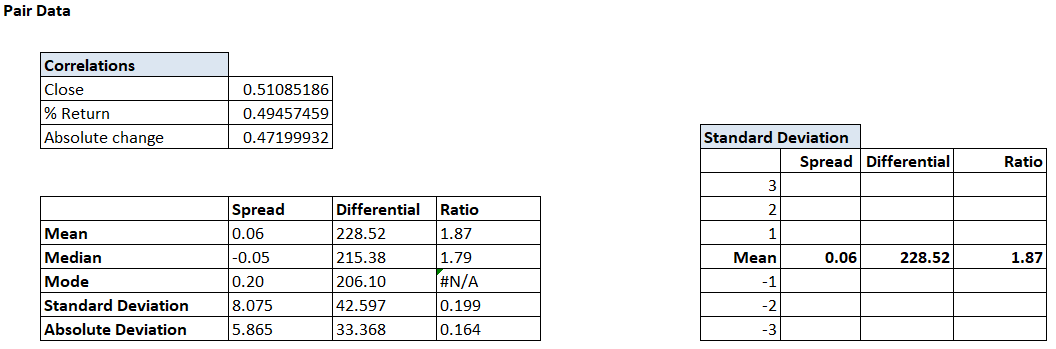
यह टेबल ऐसा दिखाई देता है 

अब हम स्प्रेड डिफरेंशियल और रेश्यो के लिए मीन के ऊपर और मीन के नीचे 1st, 2nd और 3rd स्टैंडर्ड डेविएशन के मूल्य को निकालेंगे। 

सबसे पहले स्प्रेड के डेटा पर फोकस करते हैं। स्प्रेड का मीन 0.06 है। हमें यह भी पता है कि स्टैंडर्ड देविएशन 8.075 है। 

ऐसे में, मीन के ऊपर का 1st स्टैंडर्ड डेविएशन होगा 

0.064 + 8.075 = 8.139

2nd SD –

0.064 + (2*8.075) = 16.123

3rd SD –

0.064 + (3*8.075) = 24.288

ये सब मीन के ऊपर की वैल्यू हैं। इसी तरह से हम मीन के नीचे की वैल्यू भी निकाल सकते हैं।

-1 SD –

0.064 – 8.075 = -8.011

-2 SD –

0.064 – (2*8.075) = -16.086

-3 SD –

0.064 – (3*8.075) = -24.160

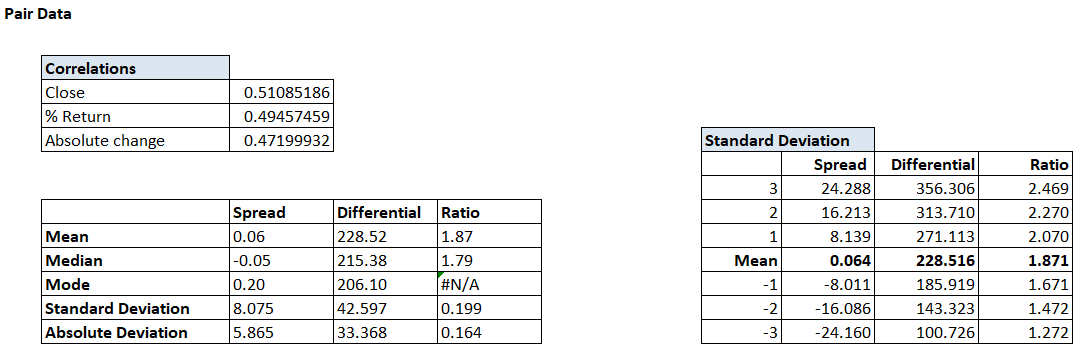
मैंने डिफरेंशियल और रेश्यो के लिए भी ये गणना कर ली है, और यह टेबल अब इस तरह का दिख रहा है –

अगर 498वां डिफरेंशियल डेटा 315 की संख्या दिखाता है तो हम बहुत जल्दी से यह समझ सकते हैं कि यह +2 स्टैंडर्ड डेविएशन के पास है और 95% भरोसे के साथ हम यह कह सकते हैं कि अगला डेटा प्वाइंट 315 से ऊपर होने की संभावना सिर्फ 5% ही है। 

तो फिलहाल हमारे पास वह सारा डेटा है जो हमें पेयर के बारे में निष्कर्ष निकालने के लिए मदद कर सकता है और यह बता सकता है कि वहां पर ट्रेड करने का मौका है या नहीं। अगले अध्याय में हम आगे बढ़ेंगे और यही करेंगे। 

यहां पर इस्तेमाल किए गए एक्सेल शीट को आप यहां से ( here.) डाउनलोड कर सकते हैं 

इस अध्याय की मुख्य बातें 

1. पेयर ट्रेडिंग में नॉर्मल डिस्ट्रीब्यूशन एक बहुत ही महत्वपूर्ण भूमिका अदा करता है 
2. 1st स्टैंडर्ड डेविएशन के अंदर आप 68% डाटा को देख सकते हैं 
3. 2nd स्टैंडर्ड डेविएशन में आप 95% डाटा को देख सकते हैं 
4. 3rd स्टैंडर्ड डेविएशन में आप 99.7% डाटा को देख सकते हैं 
5. स्टैंडर्ड डेविएशन और एब्सॉल्यूट डेविएशन के जरिए आप डेटा के वैरीएबिलिटी यानी बदलाव को नाप सकते हैं 
6. स्टैंडर्ड डेविएशन टेबल से हम मौजूदा डेटा और अनुमानित वैरिएशन की तुलना कर सकते हैं। 
7. स्टैंडर्ड डेविएशन टेबल से हमें यह संकेत मिलता है कि हम पेयर ट्रेड में लॉन्ग करेंगे या शॉर्ट करेंगे