3.1 – वैरियंस
पिछले अध्याय में हमने एक्सपेक्टेड रिटर्न की बात की थी, अब हम पोर्टफोलियो वैरियंस की बात करेंगे। पोर्टफोलियो वैरियंस हमें बताता है कि पोर्टफोलियो के स्तर पर हम कितना रिस्क उठा रहे हैं। मुझे उम्मीद है कि आप स्टैन्डर्ड डेविएशन के बारे में जानते हैं जिससे रिस्क को नापा जाता है। हमने स्टैन्डर्ड डेविएशन पर पहले कई बार अलग-अलग मॉड्यूल में चर्चा की है (मॉड्यूल 5 अध्याय 15 के बाद)। अगर आप स्टैन्डर्ड डेविएशन को नहीं समझते हैं तो मेरी सलाह यह होगी कि पहले इसके बारे में जान लीजिए। किसी एक स्टॉक से जुड़े हुए रिस्क को जानने के लिए स्टैन्डर्ड डेविएशन का इस्तेमाल आसानी से किया जा सकता है, लेकिन किसी पोर्टफोलियो का रिस्क जानना इतना आसान नहीं होता। जब आप बहुत सारे अलग-अलग स्टॉक एक साथ लाकर एक पोर्टफोलियो बनाते हैं तो रिस्क पता करना मुश्किल हो जाता है। इस अध्याय में हम इसी बात पर चर्चा करेंगे कि अपने पोर्टफोलियो के रिस्क का अनुमान कैसे लगाया जाए?
हम आगे बढ़ें, इसके पहले यह जरूरी है कि हम वैरियंस और कोवैरियंस के सिद्धांत को समझ लें। यह दोनों ही सांख्यिकी (statistical measures) से जुड़ी हुई चीजें हैं। पहले वैरियंस को समझते हैं।
किसी स्टॉक के रिटर्न का वैरियंस हमें यह बताता है कि उस स्टॉक के रिटर्न में होने वाले दैनिक औसत बदलाव और उस स्टॉक के रिटर्न में कितना अंतर है। वैरियंस निकालने का फार्मूला काफी सीधा है –
यहां,
σ2 = वैरियंस
X = दैनिक रिटर्न
µ = औसत दैनिक रिटर्न
N = देखे गए आंकड़ों/प्रेक्षणों (Observation) की संख्या
ध्यान दीजिए कि वैरियंस को सिग्मा स्क्वायर (sigma squared) के रूप में निकाला जाता है। ऐसा क्यों किया जाता है, मैं इसके विस्तार में नहीं जाऊंगा क्योंकि इसको समझाना बहुत मुश्किल है। इसलिए बस ये याद रखिए कि इसको सिग्मा स्क्वायर के रूप में निकाला जाता है। वैरियंस को निकालना काफी आसान होता है। इसे समझने के लिए यहां हम एक उदाहरण लेते हैं।
मान लीजिए किसी स्टॉक का पांच 5 दिनों का रिटर्न ऐसा दिखता है –
दिन 1 – + 0.75%
दिन 2 – + 1.25%
दिन 3 – -0.55%
दिन 4 – -0.75%
दिन 5 – +0.8%.
यहां पर औसत रिटर्न +0.3% है। अब हमें औसत रिटर्न पर हर दिन के रिटर्न में होने वाले डिस्पर्शन (Dispersion) को समझना है (मतलब ये देखना है कि हर दिन का रिटर्न औसत रिटर्न से कितनी दूर तक जाता है) और फिर उस डिस्पर्शन को स्क्वेयर करना है यानी उसका वर्ग निकालना है।
| दैनिक रिटर्न | औसत से डिस्पर्शन | डिस्पर्शन का वर्ग |
| + 0.75% | 0.75% – 0.3% = + 0.45% | 0.45%^2 = 0.002025% |
| + 1.25% | +1.25% – 0.3% = + 0.95% | 0.95%^2 = 0.009025% |
| -0.55% | -0.55% – 0.3% = -0.85% | -0.85%^2 = 0.007225% |
| -0.75% | -0.75% – 0.3% = -1.05% | -1.05%^2 = 0.011025% |
| +0.80% | +0.8% – 0.3% = +0.5% | 0.50%^2 = 0.002500% |
अब हमें इस डिस्पर्शन के वर्ग को जोड़ना है जिससे हमें 0.318000% मिलता है। जब हम इसको 5 (N) से विभाजित करेंगे तो हमें वैरियंस मिल जाएगा-
0.0318000% / 5
σ2 = 0.0063600%.
तो यह संख्या हमें बता रही है कि दैनिक रिटर्न औसत एक्सपेक्टेड रिटर्न से कितना दूर तक जा सकता है। तो एक निवेशक के तौर पर जब आप यह जानना चाहते हैं कि आपका निवेश कितना रिस्की है तो आपको वैरियंस को देखना होता है। वैरियंस जितना ज्यादा होगा आपके स्टॉक पर उतना ही ज्यादा रिस्क होगा। अगर वैरियंस कम है तो स्टॉक कम रिस्की माना जाएगा। ऊपर के उदाहरण में मैं वैरियंस को अधिक मानूंगा क्योंकि यहां पर हम सिर्फ 5 दिनों के आंकड़ों पर नजर डाल रहे हैं।
यहां पर आप शायद यह जानना चाहें- वैरियंस और स्टैन्डर्ड डेविएशन एक दूसरे से एक साधारण गणित के फॉर्मूले से जुड़े हुए हैं। देखिए-
वैरियंस का स्क्वेयर रूट = स्टैन्डर्ड डेविएशन
Square Root of Variance = Standard Deviation
आप ऊपर के उदाहरण में इस फॉर्मूले का इस्तेमाल करके स्टॉक का 5 दिनों का स्टैन्डर्ड डेविएशन निकाल सकते हैं।
%
~ 0.8%
यह स्टॉक का स्टैन्डर्ड डेविएशन यानी वोलैटिलिटी है (पिछले 5 दिनें की)। लेकिन हम यहां पर वैरियंस की बात कर रहे हैं और यह जानने की कोशिश कर रहे हैं कि इसका क्या मतलब होता है। हम आगे जाते हुए वैरियंस को कोवैरियंस के साथ जोड़ कर पोर्टफोलियो वैरियंस में इस्तेमाल करेंगे।
3.2 – कोवैरियंस
कोवैरियंस हमें बताता है कि 2 या उससे ज्यादा वेरिएबल साथ में कैसे चलते हैं? ये बताता है कि क्या वो दोनों वेरिएबल साथ साथ चलते हैं (तब यह माना जाएगा कि उनके बीच में पॉजिटिव कोवैरियंस है) या फिर दोनों वेरिएबल अलग-अलग दिशा में चलते हैं (इसका मतलब है कि वह उनके बीच नेगेटिव को कोवैरियंस है)। शेयर बाजार के संदर्भ में देखें तो कोवैरियंस हमें बताता है कि दो या उससे ज्यादा स्टॉक साथ में कैसे चलते हैं? अगर दोनों स्टॉक के बीच में पॉजिटिव कोवैरियंस है तो वह एक दिशा में चलेंगे और अगर नेगेटिव कोवैरियंस है तो वह अलग-अलग दिशा में जाएंगे।
मुझे पता है कि कोवैरियंस काफी हद तक कोरिलेशन जैसा लग रहा होगा, लेकिन ये दोनों काफी अलग हैं। इनके बीच के अंतर पर हम इस अध्याय में आगे चर्चा करेंगे।
मुझे लगता है कि जब हम 2 स्टॉक के कोवैरियंस को निकालेंगे तो फिर आपको कोवैरियंस को समझने में आसानी होगी। 2 स्टॉक का कोवैरीयंस निकालने का फार्मूला यह है-
जहां,
Rt S1 = स्टॉक 1 का दैनिक रिटर्न
Avg Rt S1 = n अवधि में स्टॉक 1 का औसत रिटर्न
Rt S2 = स्टॉक 2 का दैनिक रिटर्न
Avg Rt S2 = n अवधि में स्टॉक 2 का औसत रिटर्न
n – कुल दिनों की संख्या
दूसरे शब्दों में कहें तो, दो स्टॉक्स के बीच का कोवैरियंस को निकालने के लिए दोनों स्टॉक के दैनिक यानी डेली रिटर्न और उनके औसत रिटर्न के अंतर को निकालकर उनके जोड़ को निकालना होता है। यह समझना थोड़ा कठिन है इसलिए आइए इसको एक उदाहरण से समझते हैं।
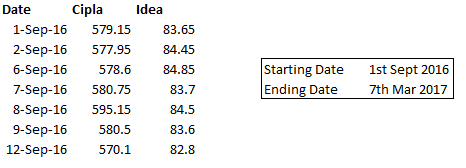
मैंने यहां पर दो स्टॉक चुने हैं – सिप्ला लिमिटेड और आइडिया सेल्यूलर लिमिटेड। इनका कोवैरियंस निकालने के लिए हमें ऊपर दिखाए गए फार्मूले का इस्तेमाल करना होगा साथ ही, इसके लिए हम माइक्रोसॉफ्ट एक्सेल का भी इस्तेमाल करेंगे।
हम आगे बढ़ें इसके पहले, आप अगर अनुमान लगाना चाहें कि सिप्ला और आइडिया के बीच में कोवैरीयंस कितना होगा? याद रखिए कि दोनों बड़ी कंपनियां हैं, करीब-करीब एक ही आकार की हैं, लेकिन दोनों अलग-अलग एक दूसरे से दूर वाले सेक्टर में काम करती हैं। आपको क्या लगता है कि इनका कोवैरियंस क्या होगा? जरा सोचिए।
एक्सेल में इनका कोवैरियंस निकालने के लिए हमें निम्न कदम उठाने होंगे। (ध्यान रहे कि एक्सेल में कोवैरियंस निकालने का सीधा सीधा तरीका भी है, लेकिन मैं थोड़ा लंबा रास्ता चुन रहा हूं जिससे आपको यह बात अच्छे से समझ में आ सके)
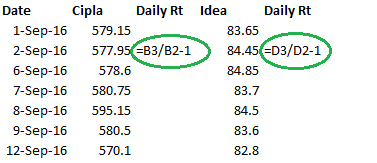
कदम 1 – स्टॉक की डेली यानी दैनिक कीमत को डाउनलोड कीजिए। आप को समझाने के लिए मैंने दोनों स्टॉक के 6 महीने के डेटा को डाउनलोड किया है।
कदम 2 – दोनों स्टॉक का डेली रिटर्न निकालिए। इसके लिए आपको स्टॉक की आज की कीमत को पिछले दिन की कीमत से विभाजित करना होगा और उससे मिली हुई संख्या में से 1 घटाना होगा।
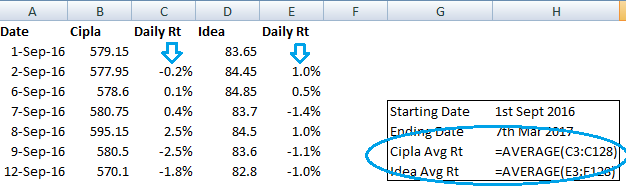
कदम 3 – अब डेली रिटर्न का औसत निकालिए
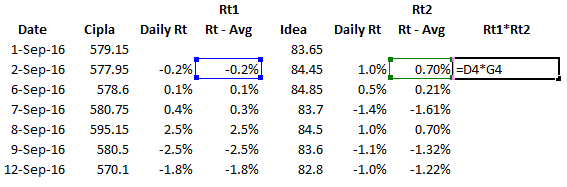
कदम 4 – एक बार औसत निकल आए तो फिर उसमें से दैनिक यानी डेली रिटर्न को घटा दें
कदम 5 – पिछले कदम में निकाले गए दोनों सीरीज को आपस में गुणा कर दें
कदम 6 – पिछले कदम में निकाली गई संख्याओं को जोड़ लें। यह जांच लें कि आपको कितने डेटा प्वाइंट मिल रहे हैं। इसके लिए आप एक्सेल के काउंट फंक्शन का इस्तेमाल कर सकते हैं। मैंने यहां तारीख की गणना की है और इसके लिए काउंट फंक्शन इस्तेमाल किया है। 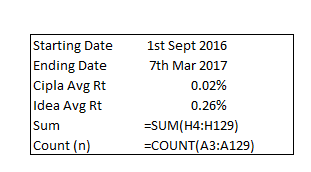
कदम 7 – कोवैरियंस निकालने के लिए यह आखिरी कदम है। अब आपको जोड़ से निकली हुई संख्या को गिनती (काउंट) से निकली संख्या से विभाजित करना है और उसमें से 1 (n-1) घटाना है। यहां पर काउंट यानी गिनती है 127, इसमें से 1 घटाने पर मिलेगा 126। पिछले कदम में जोड़ निकला है 0.006642 इसलिए कोवैरियंस होगा
= 0.006642/126
= 0.00005230
आप इस एक्सेल शीट को यहां से डाउनलोड कर सकते हैं download
जैसा कि आप देख सकते हैं कि कोवैरियंस की संख्या काफी छोटी है, लेकिन हमें उससे कोई अंतर नहीं पड़ता। हमें सिर्फ यह देखना है कि दोनों स्टॉक के बीच में पॉजिटिव कोवैरियंस है या नेगेटिव। यहां पर, इन दोनों स्टॉक के बीच में पॉजिटिव कोवैरियंस है। इसका मतलब है कि इन दोनों स्टॉक के रिटर्न एक ही दिशा में चलेंगे यानी बाजार में किसी खास स्थिति में दोनों स्टॉक की दिशा एक ही होगी। ध्यान रहे कि कोवैरियंस हमें यह नहीं बताता कि दोनों की चाल की ताकत या रफ्तार भी एक जैसी होगी या नहीं। चाल कितनी बड़ी होगी यह कोरिलेशन से पता चलता है। आइडिया और सिप्ला के बीच में कोरिलेशन 0.106 है। इसका मतलब यह है कि इनके बीच में बहुत तगड़ा कोरिलेशन नहीं है।
दोनों स्टॉक के बीच में कोरिलेशन निकालने का गणित का फॉर्मूले ये है
जहां,
Cov (x,y) दोनों स्टॉक के बीच का कोवैरियंस है
σx = स्टॉक x का स्टैन्डर्ड डेविएशन है
σy = स्टॉक y का स्टैन्डर्ड डेविएशन है
याद रहे कि किसी स्टॉक का स्टैन्डर्ड डेविएशन उसके वैरियंस का स्क्वेयर रूट होता है। यहां पर आपको एक अभ्यास देता हूं – हमने एक्सेल फंक्शन का इस्तेमाल करके सिप्ला और आइडिया के बीच में कोरिलेशन निकाला है। क्या आप इसी कोरिलेशन के फॉर्मूले का इस्तेमाल करके देख सकते हैं कि दोनों परिणामों में कोई अंतर तो नहीं है?
जब हम स्टॉक का पोर्टफोलियो बनाते हैं तो पॉजिटिव कोवैरियंस बेहतर होता है या बुरा होता है? पोर्टफोलियो मैनेजर क्या चाहते हैं कि उनके स्टॉक पोर्टफोलियो के स्टॉक के बीच में एक पॉजिटिव कोवैरियंस हो या वह ऐसा नहीं चाहते हैं? सच्चाई यह है कि पोर्टफोलियो मैनेजर हमेशा कोशिश करते हैं कि उनके स्टॉक्स के बीच में नेगेटिव कोवैरियंस हो। इसके पीछे का तर्क बहुत सीधा सा है- वह यह चाहते हैं कि ऐसी स्थिति ना आए कि उनके सारे स्टॉक्स एक ही दिशा में चलने लगें, कुछ स्टॉक अलग दिशा में भी चलने चाहिए। मतलब वह चाहते हैं कि अगर एक स्टॉक गिर रहा है तो कुछ स्टॉक तो ऐसे हों जो कि ना गिर रहे हों। इससे पोर्टफोलियो में संतुलन बना रहता है और रिस्क कम होता है।
अब एक साधारण पोर्टफोलियो की चर्चा करते हैं- इसमें 2 से ज्यादा स्टॉक होंगे, वास्तव में एक अच्छे पोर्टफोलियो में कम से कम 12 से 15 स्टॉक होंगे। अब ऐसे में कोवैरियंस कैसे निकालेंगे? आपको पोर्टफोलियो के हर एक स्टॉक का बाकी सभी दूसरे स्टॉक के साथ कोवैरियंस निकालना होगा। मैं 4 स्टॉक के पोर्टफोलियो का उदाहरण लेकर इसको दिखाता हूं। मान लीजिए पोर्टफोलियो ऐसा है
- ABB
- सिप्ला
- आइडिया
- विप्रो
ऐसी स्थिति में हमें सभी के बीच के कोवैरियंस निकालना होगा
- ABB, सिप्ला
- ABB, आइडिया
- ABB, विप्रो
- सिप्ला, आइडिया
- सिप्ला, विप्रो
- आइडिया, विप्रो
ध्यान दीजिए कि स्टॉक 1 और स्टॉक 2 के बीच में कोवैरियंस वही होगा जो कि स्टॉक 2 और स्टॉक 1 के बीच में है। तो आप देख सकते हैं कि 4 स्टॉक के पोर्टफोलियो में हमें 6 कोवैरियंस निकालने होते हैं। तो सोचिए कि अगर पोर्टफोलियो में 15 से 20 स्टॉक हों तो कितने ज्यादा कोवैरियंस निकालने होंगे? इसीलिए जब हमारे पोर्टफोलियो में 2 से ज्यादा स्टॉक होते हैं तो कोवैरियंस निकालने के लिए एक टेबल का इस्तेमाल किया जाता है जिसे वैरियंस कोवैरियंस मैट्रिक्स कहते हैं। मैं इस पर अगले अध्याय में चर्चा करूंगा।
इस अध्याय की मुख्य बातें
- स्टॉक का वैरियंस उस स्टॉक के औसत एक्सपेक्टेड रिटर्न से डिस्पर्शन मतलब दूरी को दिखाता है
- वैरियंस अधिक होता है तो रिस्क ज्यादा माना जाता है और कम वैरियंस में रिस्क कम
- वैरियंस का स्क्वायर रूट ही स्टैन्डर्ड डेविएशन होता है
- किन्हीं दो स्टॉक के बीच के रिटर्न का कोवैरियंस ये नापता है कि उनके रिटर्न किस तरीके से चलते हैं
- पॉजिटिव कोवैरियंस दिखाता है कि दोनों स्टॉक के रिटर्न एक साथ चलते हैं और नेगेटिव कोवैरियंस दिखाता है कि एक स्टॉक का रिटर्न ऊपर जाता है तो दूसरे का रिटर्न नीचे आता है
- दोनों स्टॉक के बीच का कोरिलेशन इस बदलाव के आकार यानी ताकत को बताता है
- दो स्टॉक के बीच के कोवैरियंस को उनके अपने–अपने स्टैन्डर्ड डेविएशन से विभाजित करके दोनों स्टॉक के बीच का कोरिलेशन निकाला जा सकता है
- जब पोर्टफोलियो में 2 से ज्यादा स्टॉक होते हैं तब वैरियंस कोवैरियंस मैट्रिक्स का इस्तेमाल किया जाता है



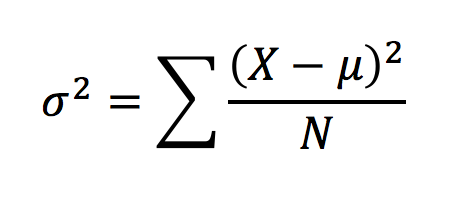
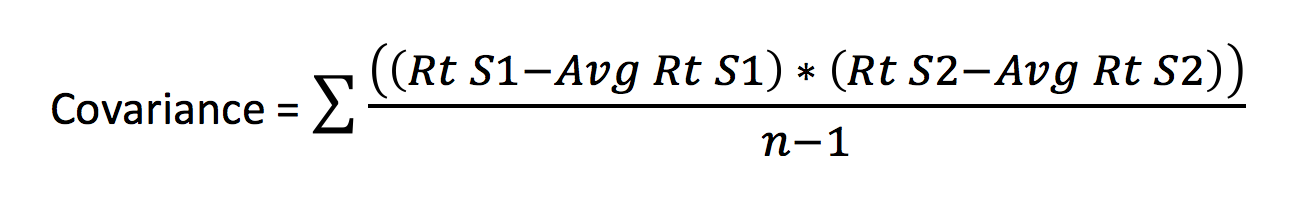



आप इस एक्सेल शीट को यहां से डाउनलोड कर सकते हैं download
Not able to download the file/excel. please assist on the same.
Hi, we are looking into this.
Options market me us kar sakate
जी हाँ
sir.,,, u use two formula for calculating \’Daily Return\’ i.e on Excel \”=LN(B2/B1)\” and \”=B2/B1-1\” Here, results similar but some difference and the Daily Average returned is a big difference between two factor so which is good to use . ?? if the difference occur the variance also differ . Standard Deviation also differ