3.1 – आज का पैसा Vs कल का पैसा

मान लीजिए आपका कोई दोस्त आपको पैसे देना चाहता है और आपके सामने दो विकल्प रखता है, जिसमें से आपको कोई एक चुनना है। 

• विकल्प 1 – वह आपको अभी ₹10,000 देगा 
• विकल्प 2 – वह आपको आज से ठीक 2 साल बाद ₹10,000 देगा 

साथ ही यह भी मान लीजिए कि आपको आज पैसों की कोई जरूरत नहीं है लेकिन ठीक 2 साल बाद आप एक नई कार खरीदना चाहते हैं। 

अब ऐसे में, क्या आप पैसे अभी ले लेंगे जबकि आपको जरूरत नहीं है या 2 साल बाद जब आपको पैसे की जरूरत होगी तब आप पैसे लेंगे। 

मुझे लगता है कि आप में से ज्यादातर लोग दूसरा विकल्प चुनेंगे। क्योंकि आज पैसे की जरूरत नहीं है इसलिए अगर आप पैसे लेंगे तो वह खर्च हो जाएंगे। इसलिए पैसे को बर्बाद होने से बचाने के लिए ज्यादातर लोग 2 साल बाद जब पैसों की जरूरत हो तभी पैसे लेना चाहेंगे।

अब मेरी सोच सही है तो आपके लिए कुछ सवाल रखता हूं – 

1. क्या पैसे की आज की कीमत की तुलना कुछ समय बाद पैसे की कीमत से की जा सकती है, मतलब आज का पैसा बनाम कल का पैसा
2. अगर हम पैसे को दो अलग-अलग समय पर नापना चाहते हैं तो उसको की तुलना करने का सही तरीका क्या होगा 

अपने दोस्त के प्रस्ताव पर सही फैसला करने के लिए आपको पता होना चाहिए कि दो अलग समय पर पैसे की कीमत की तुलना कैसे की जा सकती है। आपको पैसे की आज की कीमत की तुलना पैसे की बाद की कीमत से करना आना चाहिए। 

इस अध्याय में हम इसी को समझेंगे कि कैसे दो अलग-अलग समय पर पैसे की कीमत को नापा जा सकता है।

उम्मीद है कि इस अध्याय के अंत तक आप अपने दोस्त के इस प्रस्ताव पर फैसला लेने में पूरी तरीके से सक्षम हो जाएंगे और साथ ही जिंदगी में अपने निवेश के फैसलों के बारे में भी सही फैसला कर सकेंगे। 

यहां पर हम जिस मुख्य सिद्धांत की बात करने वाले हैं उसे टाइम वैल्यू ऑफ मनी (Time value of money /TVM) कहा जाता है। इस सिद्धांत का उपयोग वित्तीय दुनिया में कई अलग-अलग जगहों पर किया जाता है, जैसे  प्रोजेक्ट फाइनेंस, इंश्योरेंस प्लानिंग, इक्विटी डेरिवेटिव, वैल्यूएशन और पर्सनल फाइनेंस। 

टाइम वैल्यू ऑफ मनी के 2 हिस्से होते हैं। पैसे की मौजूदा वैल्यू यानी प्रेजेंट वैल्यू ऑफ मनी (Present Value of Money) और पैसे की भविष्य में कीमत यानी फ्यूचर वैल्यू ऑफ मनी (Future Value of Money)।

3.2 – प्रेजेंट वैल्यू ऑफ मनी यानी पैसे की आज की कीमत

जब हम कोई एसेट खरीदते हैं तो ये उम्मीद करते हैं कि आने वाले समय में यह हमें अच्छा रिटर्न कमा कर देगा। उदाहरण के लिए अगर हम कोई जमीन खरीदते हैं तो हम उम्मीद करते हैं कि 15 साल में इसकी कीमत एक रकम तक पहुंच जाएगी। लेकिन आज से 15 साल बाद जब मैं इस जमीन को बेचूंगा तो मुझे जो रकम मिलेगी उसकी कीमत आज की रकम की तुलना में काफी अलग होगी।

प्रेजेंट वैल्यू के सिद्धांत से आपको यह समझने में आसानी होती है कि भविष्य में आपको मिलने वाले पैसे की कीमत आज की कीमत में कितनी होगी?

थोड़ा मुश्किल है

आइए इसको एक उदाहरण से समझते हैं 

मान लीजिए कि आपने एक जमीन खरीदी है जिसकी कीमत 15,000,000 रुपए। आप इस जमीन को 15 साल तक अपने पास रखते हैं और 15 साल बाद जमीन को आप 75,000,000 रुपए में बेच देते हैं। देखने में यह काफी अच्छा लगेगा क्योंकि 15 साल में आपके पैसे 5 गुना बढ़ गए हैं। यानी 5 गुना रिटर्न मिला है। 

लेकिन यहां पर आपको अपने आप से एक महत्वपूर्ण सवाल पूछना चाहिए। 15 साल बाद आपको जो 7.5 करोड़ रुपए मिलेंगे उनकी आज की कीमत कितनी होगी? 

अगर 15 साल बाद मिलने वाले 7.5 करोड़ की कीमत आज के 1.5 करोड़ से कम हुई तो? 

इसका जवाब पाने के लिए हमें दो चीजों को समझना होगा

• आज मेरी रिस्क फ्री (risk-free) अपॉर्चुनिटी कॉस्ट (opportunity cost) क्या है? 
• रिस्क फ्री अपॉर्चुनिटी कॉस्ट के आधार पर आपको आज कितनी रकम निवेश करनी चाहिए जो कि 15 साल बाद 7.5 करोड़ हो जाए? 

इस दूसरे सवाल का जवाब ही वास्तव में वो रकम होगी जो 15 साल बाद मिलने वाले 7.5 करोड़ रुपए की कीमत के बराबर होगी। तो आइए इसका जवाब निकालते हैं 

हम 15 साल की समय अवधि की बात कर रहे हैं। 

अपॉर्चुनिटी कॉस्ट का मतलब यह होता है कि अगर इस रकम को हम जमीन खरीदने में ना लगाते तो इससे और क्या कर सकते थे। अपॉर्चुनिटी कॉस्ट निकालने के लिए हमें अर्थव्यवस्था के risk-free रेट को पता करना होगा और उसमें उसके ऊपर रिस्क प्रीमियम जोड़ना होगा। 

तो अपॉर्चुनिटी कॉस्ट का फार्मूला हुआ 

अपॉर्चुनिटी कॉस्ट = रिस्क फ्री रेट + रिस्क प्रीमियम

Opportunity cost = Risk free rate + Risk premium

रिस्क फ्री रेट वो रेट है जिस पर पैसे बिना किसी रिस्क के बढ़ते हैं। वैसे ये कहा जा सकता है कि वास्तव में रिस्क फ्री रेट जैसा कुछ भी नहीं होता, लेकिन अभी के लिए हम मान लेते हैं कि सरकार के 15 साल के बॉन्ड पर मिलने वाला रेट ही रिस्क फ्री रेट है। आमतौर पर यह माना जाता है कि सरकार अपने पेमेंट और रीपेमेंट पर किसी तरीके का डिफॉल्ट नहीं करेगी मतलब ऐसा नहीं होगा कि सरकार पैसे ना चुकाए, इसलिए सरकारी बॉन्ड के रेट को रिस्क फ्री रेट माना जा सकता है। 

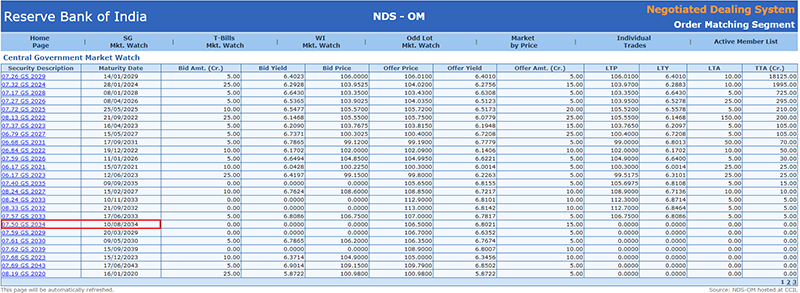
नीचे के चित्र में अभी मिल रहे सरकारी बॉन्ड की सूची दी गई है- 

क्योंकि हम 15 साल की अवधि पर नजर डाल रहे हैं इसलिए मैंने यहां 2034 के बॉन्ड को हाइलाइट किया है। जैसा कि आप देख सकते हैं कि यहां पर इसका रेट 7.5 % का है। हम यहां पर बिड-आस्क यील्ड (Bid Ask yield) पर ध्यान नहीं दे रहे हैं क्योंकि उससे हमारी गणना में मुश्किलें पैदा होंगी। जब हम बॉन्ड पर विस्तार से बात करेंगे तो इस यील्ड के बारे में विस्तार से चर्चा करेंगे। लेकिन अभी आपको यह समझना है कि अगले 15 साल के लिए रिस्क फ्री रेट 7.5 % का है। 

अपॉर्चुनिटी कॉस्ट निकालने के लिए हम इस 7.5 % में 1.5 से 2% तक का रिस्क प्रीमियम और जोड़ देते हैं। वैसे रिस्क प्रीमियम वास्तव में बहुत सारी चीजों पर निर्भर करता है लेकिन अभी हम इसे बहुत सीधा और साधारण रखा है। तो इस तरह से अब हमारी अपॉर्चुनिटी कॉस्ट होगी 

7.5 % + 1.5 %

= 9 %

तो अब हमारे पास अपॉर्चुनिटी कॉस्ट निकल चुकी है इसलिए हम अपने दूसरे सवाल का जवाब निकाल सकते हैं। मतलब हम पता कर सकते हैं कि हमें कितनी रकम को 9 % के रेट पर आज निवेश करना होगा ताकि 15 साल में 7.5 करोड़ रुपए बन जाएं। 

इस रकम को पता करने के लिए हमें कई बार गणना करनी होगी, लेकिन उसको निकालने का एक दूसरा तरीका भी है। हम इसके लिए डिस्काउंटिंग के सिद्धांत का इस्तेमाल कर सकते हैं। जिसमें हम अपने 7.5 करोड़ की रकम को 9% की दर से डिस्काउंट करेंगे। इससे हमें वह रकम पता चल जाएगी जिसको हमें निवेश करना होगा। 

अपॉर्चुनिटी कॉस्ट को जिस रेट पर डिस्काउंट किया जाता है उसे डिस्काउंट रेट कहते हैं। 

जब हम डिस्काउंटिंग करते हैं तो हम पैसे की भविष्य की वैल्यू (इस उदाहरण में 7.5 करोड़) यानी फ्यूचर वैल्यू ऑफ मनी की आज की कीमत पता कर रहे होते हैं यानी पैसे की प्रेजेंट वैल्यू को पता कर रहे होते हैं।

प्रेजेंट वैल्यू निकालने का फार्मूला है 

प्रेजेंट वैल्यू = फ्यूचर वैल्यू / (1+ डिस्काउंट रेट ) ^ (समय)

Present value = Future value / (1+ discount rate ) ^ (time)

हमें पता है कि 

• फ्यूचर वैल्यू = 75,000,000
• डिस्काउंट रेट = 9%
• समय = 15

अब प्रेजेंट वैल्यू के फार्मूले में अगर हम इन संख्याओं को डाल दें तो 

= 75,000,000 / (1+ 9%) ^ (15)

= 20,590,353

इसका मतलब है कि 75,000,000 रुपए की कीमत आज 20,590,353 होगी यानी आज के 20,590,353 अब से 15 साल बाद के 75,000,000 के बराबर हैं।

इसका मतलब यह भी हुआ कि अगर आज कोई मेरी जमीन 20,590,353 रुपए मैं खरीदना चाहे तो यह 15 साल बाद 75,000,000 रुपए के मिलने के बराबर ही है क्योंकि अगर हम 20,590,353 निवेश को अपॉर्चुनिटी कॉस्ट पर निवेश करें और 9% का अपॉर्चुनिटी कॉस्ट रखें तो इससे होने वाली कमाई 75,000,000 रुपए होगी। 

प्रेजेंट वैल्यू ऑफ मनी यानी आज की कीमत का वित्तीय दुनिया में काफी महत्व है। इसी तरह से, पैसे की फ्यूचर वैल्यू यानी फ्यूचर वैल्यू ऑफ मनी का सिद्धांत भी है। अब इसी पर चर्चा करते हैं।

3.3 – फ्यूचर वैल्यू ऑफ मनी 

फ्यूचर वैल्यू ऑफ मनी वास्तव में प्रेजेंट वैल्यू ऑफ मनी का उल्टा है। अगर हम ऊपर वाले जमीन के उदाहरण को फिर से देखें तो हमें फ्यूचर वैल्यू ऑफ मनी भी उसी सवाल का जवाब निकालने में मदद करता है 

• 20,590,353 रुपए की कीमत 15 साल में कितनी होगी? 

इस सवाल का जवाब पाने के लिए हमें अपॉर्चुनिटी कॉस्ट पता करना होगा। हम फ्यूचर वैल्यू ऑफ मनी निकाल रहे हो या प्रेजेंट वैल्यू ऑफ मनी निकाल रहे हों, दोनों में ही अपॉर्चुनिटी कॉस्ट एक ही होती है। 

तो अपॉर्चुनिटी कॉस्ट 9% होगी। 

फ्यूचर वैल्यू ऑफ मनी निकालने के लिए हमें इस रकम को अपॉर्चुनिटी कॉस्ट की दर से कंपाउंड करना होगा।

हमने पिछले अध्याय में कंपाउंडिंग का फार्मूला निकाला था

= P*(1+R)^(n),  यही फ्यूचर वैल्यू का फार्मूला भी है, इसलिए

फ्यूचर वैल्यू= P*(1+R)^(n), 

यहां,

P = रकम

R = अपॉर्चुनिटी कॉस्ट

N = समय अवधि

इस हिसाब से, 

= 20,590,353*(1+9%)^(15) 

इसका जवाब बताने के पहले आप से पूछना चाहता हूं कि आपको क्या लगता है कि जवाब क्या है?

आपको याद होगा कि हमने जब इस 75,000,000 रुपए की प्रेजेंट वैल्यू को 15 साल के लिए 9% से डिस्काउंट कर के निकाला था तो जवाब 20,595,353 आया था, अब हम इसका ठीक उल्टा करने की कोशिश कर रहे हैं यानी 20,590,353 को 9% के रेट से 15 साल के लिए कंपाउंड कर रहे हैं तो इसका जवाब 75,000,000 होना चाहिए। इस गणना का हल – 

= 20,590,353*(1+9%)^(15) 

= 75,000,000

यह रकम की फ्यूचर वैल्यू हुई।

इसका मतलब है कि आपको 15 साल बाद 75,000,000 मिले या फिर आज 20,590,353 मिले दोनों बराबर हैं।

3.4 – प्रस्ताव

इस अध्याय की शुरुआत में हमने एक उदाहरण लिया था जहां पर हमारे दोस्त ने हमें दो विकल्प दिए थे 

आपको कोई एक चुनना है। 

• विकल्प 1 – वह आपको अभी ₹10,000 देगा 
• विकल्प 2 – वह आपको आज से ठीक 2 साल बाद ₹10,000 देगा 

हमें लगता है कि आप दूसरा विकल्प चुनेंगे। लेकिन अब हमें टाइम वैल्यू ऑफ मनी पता चल चुकी है यानी पैसे की प्रेजेंट और फ्यूचर वैल्यू पता है। इसलिए अब हम अपना विकल्प बेहतर तरीके से चुन सकते हैं। 

हमें यह देखना है कि ₹10,000 की आज की वैल्यू की तुलना में ₹10,000 की 2 साल बाद की वैल्यू कहां पर है।

अगर विकल्प 1 चुनते तो हमें यह मौका मिलता है कि हम इस रकम को लेकर इसको इंटरेस्ट कमाने वाले किसी जगह पर निवेश कर दें और इस रकम को बढ़ा सकें। अभी 2 साल के फिक्स्ड डिपॉजिट पर हमें करीब-करीब 7.5% का रिटर्न मिल सकता है। तो, हमें 10,000 की 2 साल बाद की फ्यूचर वैल्यू पता करना होगा जहां पर इसकी अपॉर्चुनिटी रेट 7.5% है (यानी ये 7.5% की रेट से कंपाउंड हो रहा है)।

= 10000*(1+7.5%)^(2) 

= 11,556.25

मतलब हुआ कि अगर हम दूसरा विकल्प चुनते हैं तो हमें वास्तव में 10,000 से कम की कीमत मिल रही होगी। सही बात तब होगी जब हमें 2 साल के बाद ₹10000 की जगह ₹11556.25 मिल रहे हों। 

इससे हमें एक बड़ी सीख मिलती है जो कि फाइनेंस की दुनिया में काफी महत्वपूर्ण मानी जाती है, वह यह है कि आज आपके हाथ में जो रकम है उसकी कीमत कल मिलने वाली उसी रकम की तुलना में ज्यादा होती है क्योंकि हमारे सामने यह विकल्प होता है कि हम इस पैसे को कहीं निवेश करके रिस्क फ्री रेट पर बढ़ा सकें।

3.5 – वास्तविक दुनिया के उदाहरण

हम इस अध्याय को खत्म करें इसके पहले वास्तविक जिंदगी से जुड़े उदाहरण देख लेते हैं। यहां पर हम फ्यूचर वैल्यू और प्रेजेंट वैल्यू के सिद्धांत का इसतेमाल कर के देखेंगे। वैसे इस मॉड्यूल में आगे हम और कई बार ऐसे उदाहरण लेंगे तब आप इसे और अच्छी तरह से समझ सकेंगे।

सवाल – मान लीजिए कि आप अपनी बेटी को विदेश में पढ़ाने के लिए कुछ पैसे जमा कर रहे हैं। बेटी अभी 10 साल की है और जब वह 25 साल की हो जाएगी तब उसे अमेरिका पढ़ने जाना है। यानी आपके पास 15 साल का समय है। अमेरिका में उसकी पढ़ाई पर करीब ₹65,00,000 का खर्च आएगा। तो इस रकम तक पहुंचने के लिए आज आपके पास कितने पैसे होने चाहिए? 

जवाब – ऐसी स्थिति हो तो सबसे पहले आपको यहां प्रेजेंट वैल्यू पता करना है या फ्यूचर वैल्यू को पता करना है। इसे समझना इतना आसान नहीं होता इसलिए हमें थोड़ा और गहराई में जाना होगा इसके लिए हमें एक बार आंकड़ों को देखना होगा। 

हमें पता है कि 15 साल बाद पढ़ाई का खर्च होगा 65,00,000 रुपए। तो हमें पैसे की फ्यूचर वैल्यू पता है। 

तो हमें ये पता करना है कि हमें प्रेजेंट वैल्यू में कितनी रकम की जरूरत होगी ताकि हम इतने पैसे जमा कर सकें और अपने फ्यूचर वैल्यू तक पहुंच सकें। इसके लिए हमने प्रेजेंट वैल्यू का जो फार्मूला सीखा है उसका इस्तेमाल करना होगा – 

प्रेजेंट वैल्यू = फ्यूचर वैल्यू / (1+ डिस्काउंट रेट ) ^ (समय)

Present value = Future value / (1+ discount rate ) ^ (time)

7.5% वाले 15 साल के सरकारी बॉन्ड सके लिए सही डिस्काउंट रेट होंगे इसलिए हम उसको का इस्तेमाल करेंगे।

प्रेजेंट वैल्यू = 6,500,000 / (1+ 7.5%) ^ (15)

= 21,96,779

तो आज की वैल्यू में अगर हमारे पास ₹21,96,779 हों तो हम आसानी से 15 साल में अपने लक्ष्य तक पहुंच सकते हैं।

हो सकता है कि आप में से कुछ लोगों कि स्थिति ऐसी ही हो जहां पर आप अपने बच्चे के भविष्य के पढ़ाई के लिए पैसे जमा कर रहे हों। यहां याद रखिए कि पैसे जमा करने का यही एक तरीका नहीं है। उस रकम तक पहुंचने के बहुत सारे दूसरे तरीके भी हैं। जिन पर हम इस मॉड्यूल में आगे चर्चा करेंगे। लेकिन अभी के लिए इसे एक उदाहरण के तौर पर दिया जा रहा है ताकि आपको प्रेजेंट वैल्यू ऑफ मनी का सिद्धांत ठीक तरीके से समझ में आ सके। 

अब अध्याय को समाप्त करने के पहले हम फ्यूचर वैल्यू ऑफ मनी के लिए भी एक उदाहरण देख लेते हैं।

सवाल- आपके पिता के ऑफिस में काम करने वाले उनके दोस्त कई तरह के दूसरे काम भी करते हैं। वो हमेशा कोई न कोई वित्तीय डील बेचते रहते हैं। वो एक बार आपके घर चाय पीने आते हैं और एक वित्तीय प्रॉडक्ट बेचना चाहते हैं। वो कहते हैं कि अगर आप ₹200,000 एकमुश्त निवेश करें तो 15 साल बाद आपके परिवार को ₹450,000 मिलेंगे।

आप क्या ये निवेश करेंगे? 

जवाब – ये थोड़ा उलझाने वाला सवाल है क्योंकि इसका जवाब हमें दोनों तरीके से मिल सकता है, फ्यूचर वैल्यू निकाल कर भी और प्रेजेंट वैल्यू के सिद्धात से भी। लेकिन हम यहां पर फ्यूचर वैल्यू के तरीके का इस्तेमाल करेंगे। तो, 

आज निवेश की जाने वाली रकम – ₹200,000 

रकम की भविष्य की वैल्यू – ₹450,000 

अब हमें यह देखना है ये निवेश फायदेमंद है कि नहीं। इसके लिए हमें 200,000 की रकम को कि 7.5% की अपॉर्चुनिटी कॉस्ट के आधार पर निवेश कर के देखना होगा। 

फ्यूचर वैल्यू= 200,000*(1+7.5%)^(15) 

= 591,775.5

तो अब तुलना आपके सामने है। आप देख रहे हैं कि ₹450,000 के मुकाबले यह रकम काफी ज्यादा है। इसलिए आपको यहां पर निवेश नहीं करना चाहिए। 

यहां पर आपके लिए अभ्यास यह है कि आप इसको प्रेजेंट वैल्यू ऑफ मनी के सिद्धांत से भी निकाल कर देखिए। अपने जवाब कमेंट सेक्शन में लिखिए। 

इस अध्याय की मुख्य बातें

• पैसे की आज की वैल्यू फ्यूचर में यानी भविष्य में होने वाली वैल्यू के मुकाबले हमेशा ज्यादा होती है क्योंकि आप इस पैसे को इंटरेस्ट कमाने वाले इंस्ट्रूमेंट में  निवेश करके इस पैसे को बढ़ा सकते हैं। 
• पर्सनल फाइनेंस की दुनिया में टाइम वेल्यू ऑफ मनी सबसे महत्वपूर्ण सिद्धांतों में से एक है।
• टाइम वैल्यू ऑफ मनी में प्रेजेंट वैल्यू और फ्यूचर वैल्यू दोनों शामिल होते हैं।
• प्रेजेंट वैल्यू ऑफ मनी हमें बताती है कि भविष्य में मिलने वाली रकम की कीमत आज की तारीख में कितनी है 
• प्रेजेंट वैल्यू = फ्यूचर वैल्यू / (1+ डिस्काउंट रेट ) ^ (समय)
• डिस्काउंट रेट = अपॉर्चुनिटी कॉस्ट + रिस्क प्रीमियम 
• अगर हमें आज की रकम पता है तो उस रकम की भविष्य की कीमत निकालने के लिए फ्यूचर वैल्यू ऑफ मनी के सिध्दांत का इस्तेमाल आसानी से किया जा सकता है।
• फ्यूचर वैल्यू= P*(1+R)^(n) 
• ऊपर के फार्मूले में R अपॉर्चुनिटी कॉस्ट को बताता है, लेकिन कंपाउंड इंटरेस्ट के फार्मूले में R ग्रोथ रेट को बताता है। फ्यूचर वैल्यू और कंपाउंड इंटरेस्ट में बस इतना ही अंतर होता है।