17.1- पृष्ठभूमि
पिछले अध्याय में हमने बात की थी कि अगर निफ्टी की सालाना वोलैटिलिटी पता हो तो उसके लिए एक रेंज या दायरा कैसे बनाते हैं जिसके भीतर निफ़्टी कारोबार करेगा। हमने निफ्टी के इस रेंज के ऊपरी और निचले स्तर को निकाला भी था और हमने ये माना था कि निफ़्टी इसी दायरे के भीतर कारोबार करेगा।
लेकिन इस रेंज को लेकर हम कितने आश्वस्त हैं? क्या ऐसी कोई संभावना है कि निफ्टी इस दायरे के बाहर भी ट्रेड कर सके? अगर हाँ, तो इस बात की संभावना कितनी है कि निफ़्टी इस दायरे के बाहर ट्रेड करेगा और इस बात की संभावना कितनी है कि वह इस रेंज के भीतर रहेगा? अगर इस दायरे के बाहर रहने की भी कोई संभावना है तो उसकी कीमत कितनी होगी, मतलब निफ्टी कहां तक जा सकता है?
इन सवालों का जवाब ढूंढना काफी महत्वपूर्ण है क्योंकि इससे हम बाजार के बारे में आंकड़ों पर आधारित फैसला लेने की हालत में होंगे। यह उन फैसलों से एकदम अलग है जो आमतौर पर कोई फंडामेंटल एनालिस्ट या टेक्निकल एनालिस्ट लेता है। तो थोड़ा गहराई में जाते हैं और देखते हैं कि इन सवालों के जवाब क्या हैं?
17.2 – रैन्डम वॉक (Random Walk)
अब जो बात हम करने जा रहे हैं वह बहुत ही महत्वपूर्ण है और हमारे इस विषय से काफी ज्यादा जुड़ी हुई है। इस रोचक विषय को समझने के लिए, एक नजर डालिए नीचे के चित्र पर –
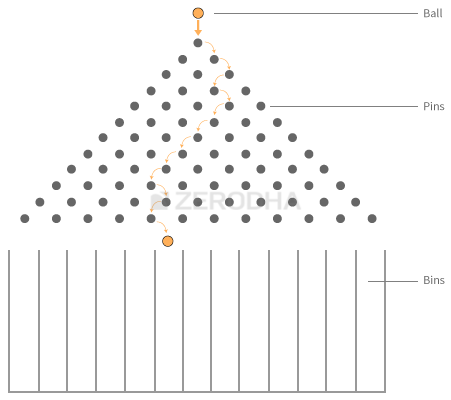
यह चित्र है गैल्टन बोर्ड (Galton Board) का । जैसा कि आप देख सकते हैं इसमें कई कीलें लगी होती हैं और नीचे कुछ बक्से बने होते हैं, जिनको कलेक्टिंग बिंस (Collecting Bins) कहते हैं।
इसमें ऊपर से बॉल गिराई जाती है जो इन कीलों के बीच से गुजरते हुए नीचे की तरफ आती है। जब बॉल गिराई जाती है तो वो पहली कील से टकराती है जिसके बाद वो किसी भी तरफ मुड़ सकती है और फिर बाकी कीलों से टकराती हुई अंत में एक किसी एक बक्से में गिरती है। इसी तरीके से इसमें बहुत ढेर सारी बॉल गिराई जाती हैं।
ध्यान दीजिए कि यहां पर जब एक बार बॉल ऊपर से गिरा दी जाती है तो आप उसका रास्ता तय करने के लिए कुछ नहीं कर सकते, वह अपने हिसाब से ही नीचे पहुंचती है। इसीलिए बॉल जो रास्ता लेती है उसको रैंडम वॉक कहते हैं। रैंडम मतलब – बेतरतीब, अनियमित या फिर बिना सोचे-समझे, वॉक (Walk) मतलब चलना, टहलना।
क्या आप यह अनुमान लगा सकते हैं कि अगर बहुत सारी बॉल एक के बाद एक गिराई जाए तो क्या होगा? हर बॉल अपने हिसाब से एक रैंडम वॉक लेगी और उसके बाद किसी एक बिन या बक्से में पहुंच जाएगी। लेकिन आपको क्या लगता है कि इन बॉल्स या गेंदों का वितरण यानी डिस्ट्रीब्यूशन कैसा होगा?
- क्या सारी बॉल एक ही बक्से में जाएंगी या
- क्या हर बक्से में बराबर बराबर बॉल जाएंगी या
- बॉल बेतरतीब तरीके से अलग-अलग बक्सों में गिरेंगी
जिन लोगों को इस प्रयोग यानी एक्सपेरिमेंट के बारे में पता नहीं है वह यह मानेंगे कि सारी बॉल अपने हिसाब से किसी भी बक्से में जाकर गिरेगी और वहां पर कोई एक निश्चित क्रम या पैटर्न नहीं होगा। लेकिन वास्तव में ऐसा नहीं होता, यहां पर एक तरीके का सिलसिला बनता है।
नीचे के चित्र पर एक बार नजर डालिए
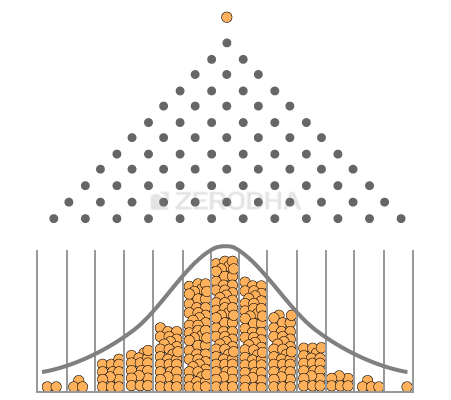
ऐसा लगता है कि जब आप बहुत सारी बॉल गैल्टन बोर्ड में डालते हैं और हर बॉल अपने हिसाब से एक रैंडम वॉक लेती है तो भी उनका वितरण एक खास क्रम से ही होता है-
- ज्यादातर बॉल बीच के बक्सों में ही जमा होती हैं
- जब आप बीच के बक्सों से बाएं या दाएं तरफ बढ़ते हैं तो वहां पर कम बॉल आती हैं
- एकदम किनारे के बक्सों में बहुत ही कम बॉल आती हैं
इस तरह के वितरण या डिस्ट्रीब्यूशन को नार्मल डिस्ट्रीब्यूशन (Normal distribution) कहते हैं। आपने स्कूल में या कहीं और बेल कर्व (Bell Curve) के बारे में जरूर सुना होगा बेल कर्व वास्तव में और कुछ नहीं सिर्फ नॉर्मल डिस्ट्रीब्यूशन होता है। सबसे खास बात यह है कि आप चाहे कितनी बार भी इस प्रयोग को करें हर बार बॉल इसी तरीके से डिस्ट्रीब्यूट यानी वितरित होती हैं जिनसे इसे नॉर्मल डिस्ट्रीब्यूशन कहा जा सके।
गैल्टन बोर्ड के इस प्रयोग को देखने और समझने के लिए आप नीचे के इस वीडियो को भी देख सकते हैं
https://youtu.be/6YDHBFVIvIs
तो अब सवाल यह है कि हम यहां पर गैल्टन बोर्ड या फिर नॉर्मल डिस्ट्रीब्यूशन की बात क्यों कर रहे हैं?
वास्तव में, हमारी आम जिंदगी में भी बहुत सारी चीजें नॉर्मल डिस्ट्रीब्यूशन के तरीके से होती हैं। उदाहरण के तौर पर –
- आप कुछ लोगों को जमा कीजिए और उनका वजन लीजिए और फिर उन सभी वजन को अलग-अलग बक्सों में या बिन (Bin) में बांट दीजिए जैसे 40 से 50 किलोग्राम, 50 से 60 किलो, 60 से 70 किलो आदि, और उसके बाद हर बक्से में आने वाले लोगों की संख्या को गिन लीजिए। आपको वहां भी नॉर्मल डिस्ट्रीब्यूशन दिखाई देगा
- यही काम आप लोगों की लंबाई के साथ भी कर सकते हैं और वहां भी आपको यही परिणाम मिलेगा
- लोगों के जूतों के साइज की बात हो
- फलों और सब्जियों के वजन की बात हो
- किसी एक खास रास्ते को तय करने में लगने वाले समय की बात हो या
- बैटरी के चलने या बैटरी के जीवन के जीवन अवधि की बात हो
हर जगह आपको नॉर्मल डिस्ट्रीब्यूशन होता दिखाई देगा। तो अगर यही नॉर्मल डिस्ट्रीब्यूशन हम शेयर बाजार में भी देखें तो- किसी शेयर के रिटर्न के पर भी लागू करने की कोशिश करें तो?
किसी भी स्टॉक या इंडेक्स का हर दिन का रिटर्न पहले से नहीं बताया जा सकता। अगर आप मुझसे पूछें कि कल TCS का रिटर्न क्या होगा तो मैं नहीं बता पाऊंगा। यह उस शेयर का एक तरीके का रैंडम वॉक है जैसे ऊपर के प्रयोग में बॉल के साथ हो रहा था। लेकिन अगर आप कुछ समय तक लगातार उसके डेली रिटर्न के आंकड़ों को जमा करें और उनके वितरण या डिस्ट्रीब्यूशन को देखें, तो आपको यहां भी नॉर्मल डिस्ट्रीब्यूशन यानी बेल कर्व बनता दिखाई देगा।
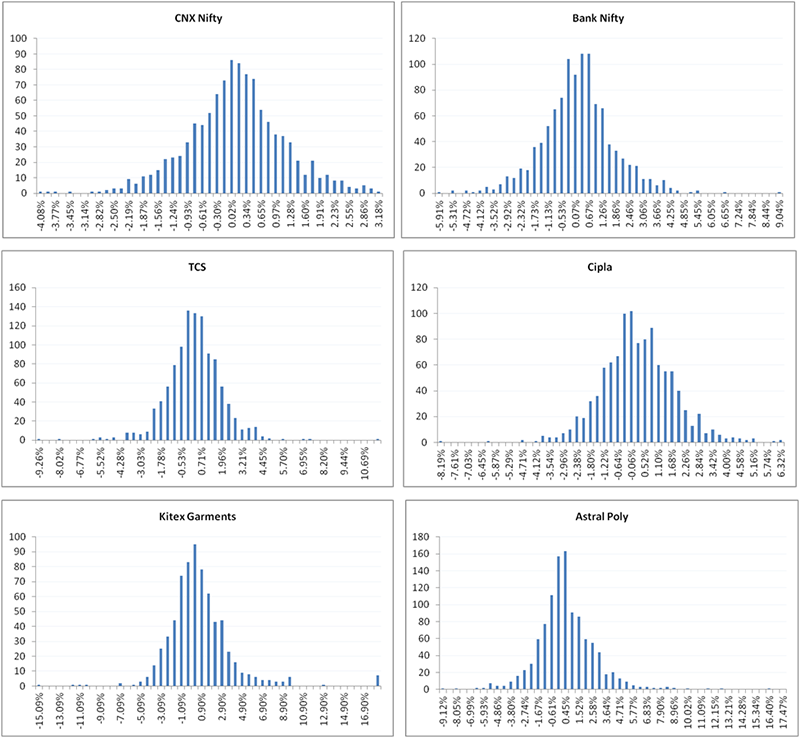
इसको और अच्छे से बताने के लिए मैंने कुछ इंडेक्स और स्टॉक्स के डेली रिटर्न का बेल कर्व बनाया है
- निफ़्टी (इंडेक्स)
- बैंक निफ़्टी (इंडेक्स)
- TCS (लार्ज कैप)
- सिप्ला (लार्ज कैप)
- किटेक्स/काईटेक्स गारमेन्ट्स- Kitex Garments (स्मॉल कैप)
- एस्ट्रेल पॉली- Astral Poly (स्मॉल कैप)
जैसा कि आप देख सकते हैं कि सभी स्टॉक्स और इंडेक्स के रिटर्न में नॉर्मल डिस्ट्रीब्यूशन दिखाई दे रहा है।
लेकिन ये महत्वपूर्ण क्यों है? इसका वोलैटिलिटी से क्या संबंध है? इसका जवाब अभी थोड़ी देर में आपको पता चल जाएगा।
17.3 – नॉर्मल डिस्ट्रीब्यूशन
पहली बार नॉर्मल डिस्ट्रीब्यूशन के बारे में जान रहे व्यक्ति के लिए ये सब समझना थोड़ा कठिन हो सकता है, इसलिए अब ऊपर किए गए नॉर्मल डिस्ट्रीब्यूशन के प्रयोग को और गैल्टन बोर्ड के प्रयोग को मैं अब स्टॉक मार्केट से जोड़ने की कोशिश करूंगा, जिससे आप इसको थोड़ा अच्छे से समझ सकें।
नॉर्मल डिस्ट्रीब्यूशन के अलावा और भी कई तरीके के डिस्ट्रीब्यूशन या वितरण हो सकते हैं। अलग-अलग तरह के आंकड़े अलग-अलग तरीके से डिस्ट्रीब्यूट यानी वितरित होते हैं। कुछ और डिस्ट्रीब्यूशन पैटर्न हैं- बाई नॉमियल डिस्ट्रीब्यूशन, यूनिफॉर्म डिस्ट्रीब्यूशन, प्वायजन डिस्ट्रीब्यूशन, ची स्क्वायर डिस्ट्रीब्यूशन (binomial distribution, uniform distribution, poisson distribution, chi square distribution ) आदि। लेकिन इन सब में सबसे ज्यादा जाना पहचाना और सब से ज्यादा रिसर्च किया हुआ डिस्ट्रीब्यूशन पैटर्न, नॉर्मल डिस्ट्रीब्यूशन ही है।
नॉर्मल डिस्ट्रीब्यूशन की अपनी कई विशेषताएं है और जिसके जरिए हम डेटा से काफी अधिक जानकारी निकाल सकते हैं। नॉर्मल डिस्ट्रीब्यूशन के कर्व को समझने के लिए दो आंकड़ों का इस्तेमाल जरूरी हैं – डिस्ट्रीब्यूशन यानी वितरण का मीन (mean) यानी माध्य और स्टैंडर्ड डेविएशन।
मीन यानी औसत/माध्य वह एक मध्य बिंदु है जहां पर ज्यादातर आंकड़े जमा होते हैं। इसे आप डिस्ट्रीब्यूशन या वितरण का औसत भी मान सकते हैं। उदाहरण के तौर पर गैल्टन बोर्ड प्रयोग में मीन या औसत वह बक्सा है जहां पर ज्यादातर बॉल आकर जमा हो रही हैं।
अब अगर हम सारे बक्सों पर नंबर डालना शुरू करें और बाएं तरफ से 1,2,3… और दाहिने तरफ से अंतिम बक्से पर 9 नंबर डालें, तो पांचवा बक्सा (जिसको यहां की लाल रंग के तीर से दिखाया गया है) वह हमारा औसत/माध्य बक्सा होगा। हमारा औसत/माध्य अगर केंद्र बिंदु है तो इसके दोनों तरफ आंकड़े या डेटा फैलाव होगा। अब आंकड़े या डेटा का यह फैलाव (इसे डिस्परशन- प्रकीर्णन/ Dispersion कहते हैं) जिस तरीके से होगा उसको बताने का काम स्टैंडर्ड डेविएशन करता है।( आपको याद होगा कि स्टैंडर्ड डेविएशन यही काम स्टॉक मार्केट में वोलैटिलिटी के लिए भी करता है)
एक और जानकारी जो आपको के पास होनी चाहिए वह यह है कि जब भी कोई स्टैंडर्ड डेविएशन (SD) की बात करता है तो वो 1st SD (स्टैंडर्ड डेविएशन) की बात कर रहा होता है। लेकिन से दूसरा स्टैंडर्ड डेविएशन (2SD) और तीसरा स्टैंडर्ड डेविएशन (3SD) आदि भी होते हैं। जब मैं SD कहता हूं तो इसका मतलब सिर्फ स्टैंडर्ड डेविएशन होता है, लेकिन जब 2SD कहा जाता है तो इसका मतलब होता है कि SD का दोगुना और जब 3SD कहा जाता है तो इसका मतलब होता है कि SD का 3 गुना और इसी तरीके से यह आगे बढ़ता जाता है।
उदाहरण के तौर पर मान लीजिए कि गैल्टन बोर्ड प्रयोग में स्टैंडर्ड डेविएशन यानी SD 1 है और औसत है 5, तब-
- 1 SD का मतलब होगा कि चौथे बक्से (5 – 1) से लेकर 6वें बक्से (5 + 1) तक के बीच में यानी औसत वाले बक्से (5) से बाएं तरफ 1 और दाएं तरफ 1 बक्सा
- 2SD का मतलब होगा तीसरा बक्सा (5 – 2) और 7वां बक्सा ( 5 + 2)
- 3SD का मतलब होगा दूसरा बक्सा (5 -3) और 8वां बक्सा(5 + 3)
अब इसके आधार पर नॉर्मल डिस्ट्रीब्यूशन का जो सामान्य सिद्धांत सामने आता है, वह है –
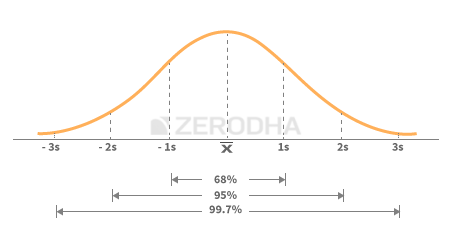
- 1st स्टैंडर्ड डेविएशन में 68% डेटा दिखता है
- 2nd स्टैंडर्ड डेविएशन में 95% डेटा दिखता है
- 3rd स्टैंडर्ड डेविएशन में 99.7% डेटा दिखता है
इसको आप नीचे के चित्र को देखकर भी समझ सकते हैं–
अब अगर हम गैल्टन बोर्ड प्रयोग में इस भी इस्तेमाल करें तो
- 1st स्टैंडर्ड डेविएशन यानी चौथे से लेकर छठवें पर बक्से तक के बीच में 68% बॉल आकर गिरेंगी
- 2nd स्टैंडर्ड डेविएशन यानी तीसरे से सातवें बक्से तक के बीच में 95% बॉल गिरेंगी
- 3rd स्टैंडर्ड डेविएशन यानी दूसरे से आठवें बक्से तक के बीच में 99.7% बॉल गिरेंगी।
अब इस को ध्यान में रखते हुए मान लीजिए कि आप एक बॉल गैल्टन बोर्ड में गिराने जा रहे हैं लेकिन उसके पहले हम एक बातचीत करते हैं-
आप – मैं एक बाल गिराने वाला हूं। क्या आप ये अनुमान लगा सकते हैं कि यह बॉल किस बक्से में जाकर गिरेगी?
मैं – नहीं मैं ये अनुमान नहीं लगा सकता क्योंकि हर बॉल एक रैंडम वॉक करती है, लेकिन मैं वह रेंज बता सकता हूं कि किन बक्सों के बीच में यह बॉल गिर सकती है।
आप – क्या आप वो रेंज बता सकते हैं?
मैं – ज्यादा संभावना इस बात की है कि यह बॉल चौथे से लेकर छठवें बक्से तक के बीच में गिरेगी।
आप – आप अपने अनुमान के बारे में कितने आश्वस्त हैं?
मैं – मैं 68% आश्वस्त हूं कि यह बॉल चौथे से छठवें बक्से के बीच में गिरेगी।
आप –68% का अनुमान थोड़ा कम भरोसे वाला है क्या आप ऐसा अनुमान बता सकते हैं जिसको लेकर आप ज्यादा आश्वस्त हों ?
मैं – मैं यह बता सकता हूं कि बॉल तीसरे से सातवें बक्से तक के बीच में गिरेगी और मैं इसको लेकर 95% आश्वस्त हूं। अगर आप इससे ज्यादा भरोसा चाहते हैं तो मैं यह कह सकता हूं कि बाल दूसरे से आठवें बक्से के बीच में गिरेगी और मैं इसको लेकर 99.5% आश्वस्त हूं।
आप – बढ़िया, इसका मतलब यह है कि इस बॉल के पहले या दसवें बक्से में गिरने की कोई संभावना नहीं है?
मैं – यह संभावना जरूर है कि यह बॉल के तीसरे SD के बक्सों के बाहर भी गिरे, लेकिन संभावना कम है।
आप – इसकी संभावना कितनी कम है?
मैं – इस बात की संभावना 0.5 प्रतिशत से भी कम है। यह एक नदी में ब्लैक स्वॉन (Black Swan) यानी काले बत्तख को देखने के बराबर है।
आप – मुझे ब्लैक स्वान स्थिति के बारे में ज्यादा बताइए।
मैं – ब्लैक स्वान इवेंट उन घटनाओं (जैसे कि बाल के दसवें पहले या 10 में बक्से में गिरना) को कहते हैं जिनकी होने की संभावना बहुत कम होती है, लेकिन जिनका होना असंभव नहीं होता। ऐसा कब होगा और कैसे होगा इसको बता पाना मुश्किल काम है, लेकिन नीचे के चित्र से आप देख सकते हैं कि यह कैसे होता है
ऊपर के चित्र में आप देख सकते हैं कि बहुत सारी बॉल गिराई गई हैं लेकिन उनमें से बहुत कम बॉल अंतिम या बाहर की तरफ से बक्सों में गिरी हैं।
17.4 – नार्मल डिस्ट्रीब्यूशन और स्टॉक का रिटर्न
उम्मीद है कि ऊपर की चर्चा से आपको नॉर्मल डिस्ट्रीब्यूशन के बारे में कुछ कुछ समझ में आ गया होगा। नॉर्मल डिस्ट्रीब्यूशन के बारे में हम बात इसलिए कर रहे हैं क्योंकि शेयर और इंडेक्स के डेली रिटर्न भी नॉर्मल डिस्ट्रीब्यूशन जैसा बेल कर्व बनाते हैं। मतलब यह कि अगर हमें पता हो कि किसी स्टॉक के रिटर्न का औसत और स्टैंडर्ड डेविएशन क्या है तो हम उस स्टॉक के रिटर्न और उसके वितरण के बारे में काफी कुछ जान सकते हैं। उदाहरण के तौर पर हम निफ्टी को लेते हैं और कुछ विश्लेषण करके देखते हैं।
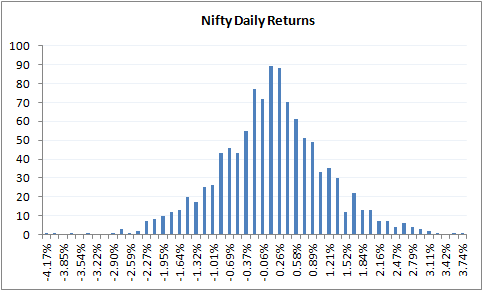
नीचे निफ्टी के डेली रिटर्न का चार्ट नीचे दिया गया है-
जैसा कि आप देख सकते हैं कि डेली रिटर्न का ये ग्राफ भी नॉर्मल डिस्ट्रीब्यूशन के ग्राफ जैसा ही दिखता है। मैंने इसका औसत/माध्य और स्टैंडर्ड डेविएशन भी निकाला है (हमने पिछले अध्याय में इसको निकालना सीखा था) आपको याद ही होना चाहिए कि इनको निकालने के लिए हमें लॉग डेली रिटर्न निकालना पड़ता है।
- डेली एवरेज / औसत (Mean) = 0.04%
- डेली स्टैंडर्ड डेविएशन / वोलैटिलिटी =1.046%
- निफ्टी की मौजूदा बाजार में कीमत = 8337
ध्यान दीजिए कि 0.04% का औसत बताता है कि निफ्टी का डेली रिटर्न 0.04% के पास है। अब इन कुछ और चीजों की गणना करते हैं –
- निफ्टी के अगले 1 साल के ट्रेड रेंज या दायरे को निकालते हैं
- निफ्टी के अगले 30 दिनों के ट्रेडिंग दायरे को निकालते हैं
इन दोनों के लिए हम 1 स्टैंडर्ड डेविएशन और 2 स्टैंडर्ड डेविएशन का इस्तेमाल करेंगे मतलब 68% और 95% भरोसे के साथ।
समाधान 1 – (1 साल के लिए निफ्टी की रेंज)
औसत = 0.04%
SD = 1.046%
अब इससे सालाना या वार्षिक आंकड़ा निकालते हैं–
औसत = 0.04*252 = 9.66%
SD = 1.046%* Sqrt (252) = 16.61%
इसके आधार पर मैं 68% भरोसे के साथ कह सकता हूं कि निफ्टी का रेंज (दायरा) होगा –
= औसत + 1 SD (उपरी रेंज) और औसत – 1 SD (निचली रेंज)
= 9.66% + 16.61% = 26.66%
= 9.66% – 16.66% = – 6.95%
ध्यान दीजिए कि यहां पर जो प्रतिशत दिखाए गए हैं वह लॉग (log) प्रतिशत हैं क्योंकि हमने इनको लॉग डेली रिटर्न के आधार पर निकाला है। अब हमें इन्हें सामान्य प्रतिशत में बदलना होगा, और उसको करते ही हमें सीधे रेंज मिल जाएगी। (निफ्टी के मौजूदा कीमत 8337 के आधार पर)
उपरी रेंज
=8337* एक्सपोनेंशियल/ exponential (26.66%)
= 10841
निचली रेंज
= 8337* एक्सपोनेंशियल/ exponential (- 6.95%)
= 7777
इस गणना से हमें पता चलता है कि निफ़्टी 7777 और 10841 के बीच में ट्रेड करेगा। मैं इस रेंज को लेकर 68% आश्वस्त हूं।
अब हम अपने भरोसे को 95% तक बढ़ाना चाहते हैं इसके लिए हम 2nd स्टैंडर्ड डेविएशन का इस्तेमाल करेंगे। देखते हैं कि हमें क्या परिणाम मिलता है-
औसत + 2 SD (उपरी रेंज) और औसत – 2 SD (निचली रेंज)
= 9.66% + 2*16.61% = 42.87%
= 9.66% – 2*16.66% = – 23.56%
इसलिए रेंज होगी –
उपरी रेंज
=8337* एक्सपोनेंशियल/ exponential (42.87%)
= 12800
और निचली रेंज
= 8337* एक्सपोनेंशियल/ exponential (- 23.56%)
= 6587
इस गणना के बाद हम 95% भरोसे के साथ कह सकते हैं कि निफ्टी 6587 और 12800 के बीच में अगले 1 साल तक ट्रेड करेगा। आप देख रहे हैं कि जब हमें ज्यादा भरोसा चाहिए तो दायरा या रेंज थोड़ा ज्यादा बड़ा हो जाता है।
आप चाहे तो 3 SD के साथ इसको 99.7% भरोसे के लिए निकाल सकते हैं।
अब मान लीजिए कि 3 SD के साथ में निफ्टी की रेंज निकालने पर निचला दायरा 5000 पर होता है (5000 मैंने ऐसे ही उदाहरण के लिए रख लिया है)। तो क्या इसका मतलब है कि निफ्टी 5000 के नीचे नहीं जाएगा? नहीं ऐसा बिल्कुल नहीं है, लेकिन निफ्टी के 5000 के नीचे जाने की संभावना काफी कम है और अगर यह 5000 के नीचे जाता है तो इसे एक ब्लैक स्वान इवेंट (Black Swan Event) कहा जाएगा। आप यही दावा ऊपरी रेंज के बारे में भी कह सकते हैं।
समाधान 2 – ( अगले 30 दिनों के लिए निफ्टी की रेंज)
हमें पता है
औसत = 0.04%
SD = 1.046%
चूंकि हमें अगले 30 दिनों का दायरा या रेंज पता करना है इसलिए हमें इस को इसी समय के हिसाब से बदलना होगा-
औसत = 0.04*30 = 1.15%
SD = 1.046%* Sqrt (30) = 5.73%
इसके आधार पर मैं 68% भरोसे के साथ कह सकता हूं कि निफ्टी का रेंज (दायरा) होगा –
= औसत + 1 SD (उपरी रेंज) और औसत – 1 SD (निचली रेंज)
= 1.15% + 5.73% = 6.88%
= 1.15% – 5.73% = – 4.58%
ध्यान दीजिए कि यहां पर जो प्रतिशत दिखाए गए हैं वह लॉग (log) प्रतिशत हैं क्योंकि हमने इनको लॉग डेली रिटर्न के आधार पर निकाला है। अब हमें इन्हें सामान्य प्रतिशत में बदलना होगा, और उसको करते ही हमें सीधे रेंज मिल जाएगी। (निफ्टी के मौजूदा कीमत 8337 के आधार पर)
उपरी रेंज
=8337* एक्सपोनेंशियल/ exponential (6.88%)
= 8930
निचली रेंज
= 8337* एक्सपोनेंशियल/ exponential (- 4.58%)
= 7963
तो अब हम 68% भरोसे के साथ कह सकते हैं कि निफ्टी अगले 30 दिनों में 8930 और 7963 के बीच में ट्रेड करेगा।
अब हम अपने भरोसे को 95% तक बढ़ाते हैं इसके लिए हम 2nd स्टैंडर्ड डेविएशन का इस्तेमाल करेंगे। देखते हैं कि हमें क्या परिणाम मिलता है-
औसत + 2 SD (उपरी रेंज) और औसत – 2 SD (निचली रेंज)
= 1.15% + 2*5.73%% = 12.61%
= 1.15% – 2*5.73% = – 10.31%
इसलिए रेंज होगी –
उपरी रेंज
=8337* एक्सपोनेंशियल/ exponential (12.61%)
= 9457
और निचली रेंज
= 8337* एक्सपोनेंशियल/ exponential (- 10.31%)
= 7520
मुझे उम्मीद है कि गणना आप को ठीक से समझ में आ रही है आप चाहे तो इसका एक्सेल शीट (जिस पर मैंने गणना की है) यहां से download कर सकते हैं।
अब यहां पर आपके दिमाग में यह सवाल आ सकता है कि – नॉर्मल डिस्ट्रीब्यूशन तो ठीक है, समझ में आ गया। लेकिन मैं इसको अपने ट्रेड के लिए कैसे इस्तेमाल करूंगा? इसको हम अगले अध्याय में समझेंगे। अगले अध्याय में हम स्टैंडर्ड डेविएशन यानी वोलैटिलिटी और ट्रेडिंग में इसके महत्व को भी जानेंगे । दो और बातें जो हम और भी जानेंगे 1) नॉर्मल डिस्ट्रीब्यूशन का इस्तेमाल करके बेचने के लिए सही स्ट्राइक कैसे चुने और 2) वोलैटिलिटी का इस्तेमाल करके अपने लिए स्टॉप लॉस कैसे तय करें।
लेकिन याद रखिए अंततः हमें वेगा को समझना है और ऑप्शन प्रीमियम पर इसके असर को जानना है।
इस अध्याय की मुख्य बातें
- किसी भी स्टॉक का डेली रिटर्न एक रैंडम वॉक होता है जिसको बता पाना काफी मुश्किल है।
- किसी भी स्टॉक का रिटर्न आमतौर पर नॉर्मल डिस्ट्रीब्यूशन के तरीके से ही होता है।
- नॉर्मल डिस्ट्रीब्यूशन में डेटा एक औसत के आस पास होता है और औसत से उसकी दूरी या बदलाव को स्टैंडर्ड डेविएशन से नापा जा सकता है।
- 1st SD से हम 68% तक का डेटा देख सकते हैं।
- 2nd SD से हम 95% तक का डेटा देख सकते हैं।
- 3rd SD से हमें 99.5% डेटा के बारे में पता चलता है।
- 3rd SD के डेटा के बाहर जो कुछ होता है उसे ब्लैक स्वान इवेंट कहते हैं।
- SD के आधार पर हम किसी स्टॉक या इंडेक्स के ऊपरी और निचले रेंज को पता कर सकते हैं।





Sir 1st time 1 month ka range nikal kr check kr skte hai ya daily range calculate krna padega
YOu can do it one time and see how its going, otherwise you can make small changes to it and optimize.
download excel link not working
Sir
Excel calculation file is not download able pls help
Ma\’am I kindly request you jo bhi calculation apne is chapter mien bataya hai usko ek baar Hindi mien video ke through step by step karke bta dijiye zerodha varsity ke you tube channel par.
Please check Varsity Youtube channel, we have content in Hindi as well – https://www.youtube.com/@varsitybyzerodha
a lot of wrong calculation
Isme jo. 004% h average ye kese nikala gya h?
हमने इसको इसी अध्याय में समझाया है।
औसत = 0.04*30 = 1.15% how to calculate this answer please explain
औसत = 0.04*252 = 9.66% iska answer 9.66% kaise aya , mera answer to 10.08 nikal raha hai. please explain
= 9.66% + 16.61% = 26.66%
= 9.66% – 16.66% = – 6.95%
Nichali line 16.66 ki jagah 16.61 hona chahiye
सूचित करने के लिए धन्यवाद।
= 9.66% + 16.61% = 26.66%
= 9.66% – 16.66% = – 6.95%
Nichali line 16.66 ki jagah 16.61 hain
औसत + 2 SD (उपरी रेंज) और औसत – 2 SD (निचली रेंज)
= 9.66% + 2*16.61% = 42.87%
= 9.66% – 2*16.66% = – 23.56%
इसलिए रेंज होगी –
उपरी रेंज
=8337* एक्सपोनेंशियल/ exponential (42.87%)
= 12800
और निचली रेंज
= 8337* एक्सपोनेंशियल/ exponential (- 23.56%)
= 6587
अब हमें इन्हें सामान्य प्रतिशत में बदलना होगा, और उसको करते ही हमें सीधे रेंज मिल जाएगी। (निफ्टी के मौजूदा कीमत 8337 के आधार पर)
उपरी रेंज
=8337* एक्सपोनेंशियल/ exponential (26.66%)
= 10841
How?
Pls explain
हमने सब कुछ इसी अध्याय में समझाया है, कृपया इसको पूरा पढ़ें।
8337*EXPONENTIAL(26.66) = 10841 SIR ISS FORMULA KO THODA OR CLARYFI KR DETE TO BADIYA REHTA .THANK YOU..
9.66%+16.61%=26.66% YE 26.66% ANKDA KESE AAYA .THODA DOUBT THA YHA PR.MERE HISAB SE YHA PR.26.27%ANA CHAHIYE AGAR ME RIGHT HU TO.TO PLEASE YHA PR THODA DOUBT CLEAR KARE .THANK YOU.
Content in the Zerodha Varsity about stock market is one of the best online knowledge platform I ever meet.
आपका धन्यवाद।
औसत = 0.04%
SD = 1.046% यहां पर SD कैसे निकाला है औसत का
हमने इसको इसी अध्याय में समझाया है कृपया इसको पूरा पढ़ें।
ध्यान दीजिए कि 0.04% का औसत बताता है कि निफ्टी का डेली रिटर्न 0.04% के पास है। ये कही पे भी कैल्कुलेट नही करके बताया है।
हमने इसको इसी अध्याय में समझाया है कृपया इसको पूरा पढ़ें।
Hi,
जैसे English कंटेंट मे नीचे Download PDF का option होता है। वैसे हिंदी कंटेंट के एंड मे नीचे मे Download हिंदी PDF का option missing है। Kindly thankful
जल्द ही उपलब्ध कराया जायेगा।
Please provide me range formula mam this formula is not working because that\’s are different from each other
Hi Umar, this is relevant to the content inside the chapter, please read the full chapter to understand more.
test\”>OOO
Sir exponential calculations mining
Examples 8337*exponential (-23.56%)
Ans = 6587
Exponential kiya he sir
Phillies reply
Sir
6355482080 contect
हमने इसको इसी अध्याय में समझाया है कृपया इसको पूरा पढ़ें।
=8337* एक्सपोनेंशियल/ exponential (6.88%)
आपने इस्को केसे किया मतलब ये 8337*(6.88%) का उत्तर 8930 नहीं आ रहा
Mean 0.04 kaha se aaya ye samjh me nahi aa raha hai
Excel sheet to find range of NIFTY is not downloadable.
There seems to be no issue, we could download it, please retry 🙂
अब इससे सालाना या वार्षिक आंकड़ा निकालते हैं–
औसत = 0.04*252 = 9.66% yaha par 252 kyu liya gaya hai 365 ke badle mai
Hi Ahmad, 252 उस वर्ष की ट्रेडिंग डेज (दिनों) की संख्या है।
To iss hisab se 30 din ka data 30 din naa hokar agle 20-22 trading days hona chahiye?
plz explain calculation
We\’ve explained it in this module 🙂
jii mera ek doubt h agr kisi stock ka normal distribution check karna ho 1 month ka to uska spot price hum kis base pe calculate krenge..??
हमने इसमें एक्सेल दिया इसका जवाब आपको वहां पर मिलजायेगा।
You really doing a good job, 0 idea wala bhi bahut kuch sikh sakta hai.
Thank you so much
आपका धन्यवाद 🙂
Dear sir/madam
Excel sheet me 3/10/2011 se 7/28/2015 ka return nikala gya hai 252 days ka Kyu nhi. Pls reply fast. Mein bhut confuse ho rha hu.
यह डाटा हर साल के लिए कैलकुलेट किया गया है।
Hello , Thanks For sharing this wonderful knowledge in such simple way !
Is topic me aapane range Nikal ne ke liye average/mean + SD/volatility kyu liya?? Jab ke apnea previous
Chapter me aapne SD or Volatility Se range nikal ne ke 2 methods sikhaye the .
Ab sir kis method se range nikal na better hoga , kyu ki me jyadatar option sell Karne me interested hu .
दोनों ही मेथड्स सही काम करेंगे, आप को जो उपयोग करने में आसान लगे उसी को इस्तेमाल करें।
उपरी रेंज
=8337* एक्सपोनेंशियल/ exponential (42.87%)
= 12800
और निचली रेंज
= 8337* एक्सपोनेंशियल/ exponential (- 23.56%)
= 6587
ye value kese ayi plzz clear kare.!
इसके गणित में हमने फार्मूला इस्तेमाल किया है जो उसी अध्याय में उपलब्ध है।
Excellent and very useful knowledge share by team. Thank you for this and If u have any latest study material then please share.
We are working on it, it will be soon made available.
चूंकि हमें अगले 30 दिनों का दायरा या रेंज पता करना है इसलिए हमें इस को इसी समय के हिसाब से बदलना होगा-
औसत = 0.04*30 = 1.15% wrong multiple
This is equal to 1.2%
Please explain
यह गणित में कुछ गलत होगा, हम इसको चेक करेंगे।
1 saal k range k liye 252 aur monthly k liye 30 kui multiple kiya thora clear kare..
यह हमने बाकि के अध्यायों में समझाया है, कृपया इसको पूरा पढ़े।
Thanks, I got the answer from questionnaires…
okay 🙂
अब इससे सालाना या वार्षिक आंकड़ा निकालते हैं–
औसत = 0.04*252 = 9.66%
SD = 1.046%* Sqrt (252) = 16.61%
this 252 is Nifty working day in a year ? please confirm.
Bin width 50 divided kaise he
(Min-max)/50 (binwidth)
आपका सवाल समझ नहीं आया, क्या आप विस्तार में बता सकते हैं?
How calculate daily return?
आपके शेयर के ओपनिंग या क्लोजिंग प्राइस का डिफरेंस निकालिये आप अपना डेली P&L भी चेक कर सकते हैँ ।
(ध्यान दीजिए कि यहां पर जो प्रतिशत दिखाए गए हैं वह लॉग (log) प्रतिशत हैं क्योंकि हमने इनको लॉग डेली रिटर्न के आधार पर निकाला है। अब हमें इन्हें सामान्य प्रतिशत में बदलना होगा) ???? sir how can we change log daily return in normal percentage ????
अध्याय के बाकी के हिस्से मे यह समझाया गया कृपया उसको पूरा पढ़ें।
मुझे उम्मीद है कि गणना आप को ठीक से समझ में आ रही है आप चाहे तो इसका एक्सेल शीट (जिस पर मैंने गणना की है) यहां से डाउनलोड कर सकते हैं।
कृपया लिंक प्रदान करें.
धन्यवाद…!
सूचित करने के लिए धन्यवाद हमने इसको ऐड करदिया है.
उपरी रेंज
=8337* एक्सपोनेंशियल/ exponential (6.88%)
= 8930
निचली रेंज
= 8337* एक्सपोनेंशियल/ exponential (- 6.95%)
= 7777
how its possible pls explain
हम इस गणित को अंडरलाइंग के एक टाइम फ्रेम का पॉसिबल रेंज जान्ने के लिए करते हैं। आप इस रेंज को ऑप्शन स्ट्राइक्स जो बेचने के लिए आकर्षित हो उनको ढूंढ़ने के लिए इस्तेमाल कर सकते हैं।
Dear Sir,
I\’m greatfull to study this topic provided by you, this a mind blowing explanation in very simple way.
so, Thanks a lot for your work which very useful to us to increase level of stocke market knpwledge.
Thanks and regards,
Urmender singh
मुझे उम्मीद है कि गणना आप को ठीक से समझ में आ रही है आप चाहे तो इसका एक्सेल शीट (जिस पर मैंने गणना की है) यहां से डाउनलोड कर सकते हैं।
कृपया लिंक प्रदान करें.
धन्यवाद…!
अब इससे सालाना या वार्षिक आंकड़ा निकालते हैं–
औसत = 0.04*252 = 9.66% yaha par 252 kyu liya gaya hai 365 ke badle mai.
Hi Ahmad, 252 उस वर्ष की ट्रेडिंग डेज (दिनों) की संख्या है।
2SD का मतलब होगा तीसरा बक्सा (5 – 3) और 7वां बक्सा ( 5 + 2)
सर यहाँ बक्सा (5-3) के स्थान पर (5-2) होना चाहिए।
हमने इसको सही करदिया है, धन्यवाद।