5.1 – कोरिलेशन मैट्रिक्स
पिछले अध्याय में हमने वैरियंस कोवैरियंस मैट्रिक्स निकाला था। जैसा कि हमने कहा था कि इसमें मिलने वाली संख्या इतनी छोटी होती है जिससे कोई अर्थ निकालना मुश्किल होता है, इसीलिए आमतौर पर वैरियंस कोवैरियंस मैट्रिक्स के बाद साथ में कोरिलेशन मैट्रिक्स निकाला जाता है।
तो आगे बढ़ते हैं और कोरिलेशन मैट्रिक्स निकालते हैं।
किन्हीं दो स्टॉक के बीच में कोरिलेशन कैसे निकाला जाता है, हमने इसका फार्मूला पिछले अध्याय में भी बताया था। एक बार फिर देख लीजिए
जहां,
Cov (x,y) दो स्टॉक के बीच का कोवैरियंस है
σx = स्टॉक x का स्टैन्डर्ड डेविएशन
σy = स्टॉक y का स्टैन्डर्ड डेविएशन y
अगर आपके पोर्टफोलियो में दो स्टॉक हैं तो यह फार्मूला बहुत अच्छे से काम करता है। लेकिन हमारे पोर्टफोलियो में पांच स्टॉक हैं, इसलिए हमें कोरिलेशन निकालने के लिए मैट्रिक्स ऑपरेशन करना पड़ेगा। जब किसी पोर्टफोलियो में कई स्टॉक होते हैं तो उसका कोरिलेशन निकालने के लिए सभी स्टॉक के कोरिलेशन को n x n के मैट्रिक्स में रखना पड़ता है। जैसे हमारे पोर्टफोलियो में 5 स्टॉक हैं तो हमें 5 x 5 का मैट्रिक्स तैयार करना होगा।
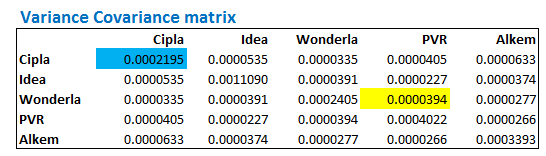
कोरिलेशन निकालने का फार्मूला वही रहता है। पिछले अध्याय में बनाए गए वैरियंस कोवैरियंस मैट्रिक्स के चित्र पर फिर से नजर डालिए –
तो हमें इस तरह इस मैट्रिक्स से फॉर्मूले में दिखाए गए विभाजन के लिए ऊपर का अंक (Numerator) तो मिल गया, अब विभाजन के नीचे का हिस्सा (denominator/डिनॉमिनेटर) निकालना है, जो कि वास्तव में स्टॉक A के स्टैन्डर्ड डेविएशन को स्टॉक B के स्टैन्डर्ड डेविएशन से विभाजित करके मिलने वाली संख्या है। अगर पोर्टफोलियो में 5 स्टॉक हैं तो हमें उस उन पांचों स्टॉक के जितने भी जोड़े बन सकते हैं उन सभी जोड़ों के लिए इसी तरीके से स्टैन्डर्ड डेविएशन निकालना होगा।
तो आइए आगे बढ़ते हैं और इसे करते हैं।
सबसे पहले हमें पोर्टफोलियो के सभी स्टॉक के लिए स्टैन्डर्ड डेविएशन निकालना होगा। मुझे उम्मीद है कि आपको यह करना आता है। आपको सिर्फ एक्सेल में डेली रिटर्न ऐरे (array) में ‘=Stdev()’ के जरिए स्टैन्डर्ड डेविएशन निकालना है।
मैंने इसको एक एक्सेल पर पिछले अध्याय में निकाला था उस चित्र को फिर से से दे रहा हूं
अब हमारे पास सभी स्टॉक का अलग-अलग स्टैन्डर्ड डेविएशन है। अब हमें सभी संभावित जोड़ों के स्टैन्डर्ड डेविएशन का प्रॉडक्ट निकालना है। इसके लिए हमें मैट्रिक्स मल्टीप्लिकेशन करना होगा। ये बहुत ही आसान है, बस स्टैन्डर्ड डेविएशन ऐरे (array) को उसके ट्रांसपोज से गुणा करना होगा।
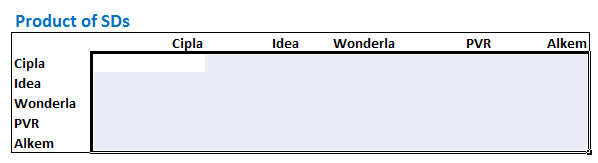
इसके लिए पहले हम मैट्रिक स्केल्टन (skeleton/ ढांचा) बनाते हैं और सभी सेल (Cell) को हाईलाइट कर के रखेंगे।
इसके बाद सेल को बिना डिसेलेक्ट किए हुए हम मैट्रिक्स मल्टीप्लिकेशन फंक्शन करेंगे। ध्यान दीजिए कि हम स्टैन्डर्ड डेविएशन ऐरे (array) को उसके अपने ट्रांसपोज से गुणा कर रहे हैं। नीचे के चित्र पर नजर डालिए तो आपको यह समझ में आएगा। साथ ही चित्र में दिए गए फॉर्मूले पर भी नजर रखिए।
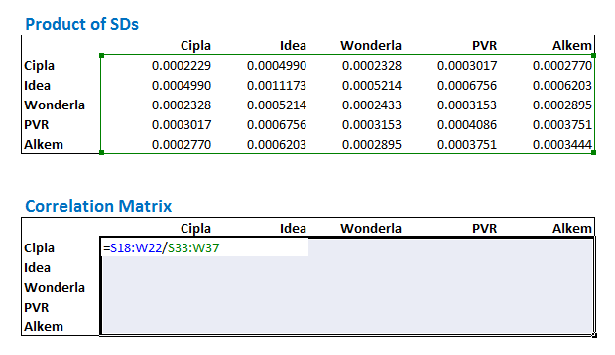
जैसा कि मैंने पिछले अध्याय में भी कहा था कि जब भी आप मैट्रिक्स या ऐरे (array) फंक्शन का एक्सेल में इस्तेमाल करते हैं तो आपको कंट्रोल+शिफ्ट+एंटर (Ctrl +Shift +Enter) एक साथ दबाना है। इससे आपको एक ऐसा मैट्रिक्स मिलेगा
अब एक बार फिर से कोरिलेशन के फार्मूले पर नजर डालिए
तो अब इस विभाजन में ऊपर का हिस्सा हमें नीचे के वैरियंस कोवैरियंस मैट्रिक्स में दिख रहा है जबकि इस विभाजन में नीचे का हिस्सा स्टैन्डर्ड डेविएशन के उस कैलकुलेशन से निकला है जिसको हमने अभी ऊपर किया है।
वैरियंस कोवैरियंस मैट्रिक्स को स्टैन्डर्ड डेविएशन के विभाजन से निकले नतीजे से विभाजित करेंगे तो हमें कोरिलेशन मैट्रिक्स मिलता है। ध्यान दीजिए कि यहां हर आंकड़ा अलग-अलग विभाजित किया जाता है यानी यह एक तरीके का ऐरे (array) फंक्शन है जिसमें हमें कंट्रोल+शिफ्ट+एंटर (Ctrl +Shift +Enter) दबाना होगा।
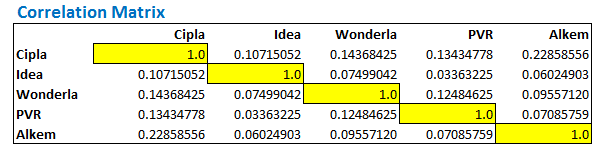
इससे मिलने वाला कोरिलेशन मैट्रिक्स कुछ ऐसा दिखेगा
कोरिलेशन मैट्रिक्स हमें दो स्टॉक के बीच में कोरिलेशन को दिखाता है। उदाहरण के तौर पर, अगर मुझे सिप्ला और एल्केम के बीच में कोरिलेशन को देखना है, तो हमें देखना होगा कि इन दोनों यानी सिप्ला और एल्केम के नाम के सामने आपस में मिलने वाले सेल कौन से हैं और उनमें कौन सी संख्या है। इसको करने के दो तरीके हैं
- सिप्ला के रो (row) को देखें और वहां से सीधे एल्केम के कॉलम (column) तक जाएं
- एल्केम के रो देखें और सिप्ला के कॉलम तक जाएं
इन दोनों में आपको एक ही परिणाम मिलेगा – 0.2285, आपको पता ही है कि स्टॉक A और स्टॉक B के बीच का कोरिलेशन वैसा ही होगा जैसा स्टॉक B और स्टॉक A के बीच का होगा। इसी वजह से मैट्रिक्स में आपको एक जैसे परिणाम दो जगहों पर देखने को मिलेंगे, पीले रंग के सेल से बन रही तिरछी रेखा के दोनो तरफ। नीचे के चित्र पर नजर डालिए मैंने सिप्ला और एल्केम के कोरिलेशन और एल्केम और सिप्ला के कोरिलेशन को हाईलाइट किया है –
बीच में पीले रंग से हाईलाइट किए गया कोरिलेशन उस स्टॉक का अपने साथ का कोरिलेशन है। यहां पर आपको ये भी दिखेगा कि पीले रंग से हाईलाइट किए गए सेल के ठीक नीचे जो संख्या है वही संख्या अगले कॉलम में पीले रंग से हाईलाइट सेल के ठीक ऊपर है।
ये भी साफ है कि स्टॉक A और स्टॉक A के बीच का कोरिलेशन हमेशा 1 होता है, इसी को पीले रंग से हाईलाइट किया गया है।
5.2 पोर्टफोलियो वैरियंस
अब हम पोर्टफोलियो वैरियंस निकालने से कुछ ही कदम दूर हैं। जैसा कि हम पहले भी चर्चा कर चुके हैं कि पोर्टफोलियो वैरियंस निकाल कर ही हम यह पता कर सकते हैं कि हमारे पोर्टफोलियो पर हम कितना रिस्क ले रहे हैं। इसके आधार पर ही हम अपना निवेश कर सकते हैं नहीं तो हम अंधेरे में ही तीर चलाते रहेंगे। ये पता करके हम और भी अधिक जानकारी के साथ निवेश कर सकेंगे। हम इसके बारे में आगे और भी चर्चा करेंगे।
पोर्टफोलियो वैरियंस निकालने के पहले कदम के तौर पर हमें हर स्टॉक को एक वेट (weight) यानी वजन देना होगा, यह और कुछ नहीं सिर्फ पोर्टफोलियो में उसका हिस्सा है। इसमें यह तय करना होता है कि हर स्टॉक में हम कितने पैसे निवेश करने जा रहे हैं। उदाहरण के तौर पर अगर मेरे पास ₹100 हैं और मैं यह सारे ₹100 एक ही स्टॉक में लगाने जा रहा हूं तो इसका मतलब है कि उस स्टॉक का वेट यानी वजन 100% है। इसी तरीके से अगर मैं उस ₹100 में से ₹50 एक स्टॉक में, ₹20 दूसरे स्टॉक में और ₹30 तीसरे स्टॉक में लगाने जा रहा हूं तो इन तीनों का वजन यानी वेट 50% 20% और 30% होगा।
तो अब मैं अपनी मर्जी के हिसाब से अपने पोर्टफोलियो के पांचों स्टॉक को अलग-अलग वेट दे देता हूं।
- सिप्ला @ 7%
- आइडिया @ 16%
- वंडरला @ 25%
- PVR @ 30%
- एल्केम @ 22%
यहां पर अलग-अलग वेट या वजन देने के पीछे कोई भी विज्ञान नहीं है, लेकिन यह कैसे होता है इस पर हम इस मॉड्यूल में आगे चर्चा करेंगे।
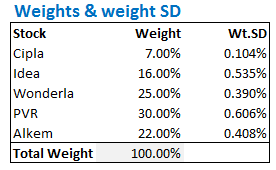
अब अगला कदम है कि हम इन सब का वेटेड स्टैन्डर्ड डेविएशन (weighted standard deviation) निकालना, इसका मतलब है कि हमें हर स्टॉक के वेट (वजन) को उसके स्टैंडर्ड डेविएशन से गुणा करना होगा। उदाहरण के तौर पर सिपला का स्टैन्डर्ड डेविएशन 1.49% है इसलिए इसका वेटेड स्टैन्डर्ड डेविएशन होगा 7% * 1.49% = 0.10%.
अब हम पांचों स्टॉक के वेट और उनके वेटेड स्टैंडर्ड डेविएशन पर नजर डालते हैं
ध्यान रहे कि कुल वेट यानी कुल वजन 100% ही होना चाहिए मतलब सभी स्टॉक के वजन को मिला कर 100 की संख्या आनी चाहिए।
अब हमारे पास टुकड़ों में वो सारी जानकारी है जिसके आधार पर हम पोर्टफोलियो वैरियंस निकाल सकते हैं। पोर्टफोलियो वैरियंस निकालने का फार्मूला नीचे दिया गया है –
पोर्टफोलियो वैरियंस = Sqrt (ट्रांसपोज (Wt.SD) * कोरिलेशन मैट्रिक्स * Wt. SD)
Portfolio Variance = Sqrt (Transpose (Wt.SD) * Correlation Matrix * Wt. SD)
जहां,
Wt. SD = वेट स्टैन्डर्ड डेविएशन ऐरे (weights standard deviation array)
इस फॉर्मूले को हम तीन कदमों में लागू करेंगे
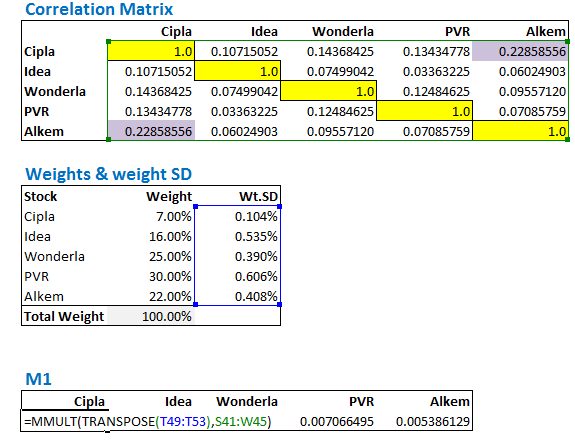
- Wt. SD के ट्रांसपोज और कोरिलेशन मैट्रिक्स को गुणा करेंगे, इससे हमें 5 अवयवों (Elements) वाला मैट्रिक्स मिलेगा।
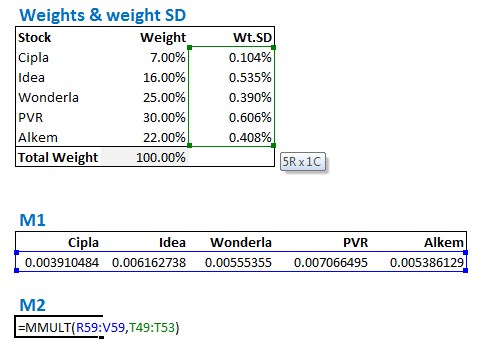
- ऊपर मिले परिणाम (row matrix) को वेट स्टैन्डर्ड डेविएशन ऐरे (weights standard deviation array) से गुणा करेंगे तो हमें एक संख्या मिलेगी
- अब ऊपर निकाले गए इस परिणाम का वर्गमूल यानी स्क्वैयर रूट (square root) निकालेंगे तो हमें पोर्टफोलियो वैरियंस मिलेगा
तो, आइए अब सीधे इस तरह से पोर्टफोलियो वैरीयंस निकालते हैं –
मैं एक 5 अवयवों (element) वाला एक रो मैट्रिक्स बना कर उसे ‘M1’ नाम देता हूं। ये Wt. SD के ट्रांसपोज और कोरिलेशन मैट्रिक्स को गुणा से मिलने वाला परिणाम है।
ध्यान रखें कि आपको खाली ऐरे (array) स्थान को सेलेक्ट करना है और कंट्रोल+शिफ्ट+एंटर (Ctrl +Shift +Enter) एक साथ दबाना है।
अब हम M2 तैयार करेंगे जो कि M1 और स्टैन्डर्ड डेविएशन को गुणा करके मिलेगा।
हम M2 का मूल्य निकालेंगे जो कि 0.000123542 है, इसका वर्गमूल यानी स्केवैयर रूट ही पोर्टफोलियो वैरियंस होगा
इस गणना से हमें नतीजा मिलेगा 1.11%, जो कि इन पांच स्टॉक के पोर्टफोलियो का पोर्टफोलियो वैरियंस होगा।
अब यहां पर थोड़ा आराम करते हैं। बाकी सब अगले अध्याय में।
इस अध्याय में इस्तेमाल हुए एक्सेल शीट को आप यहां से Download डाउनलोड कर सकते हैं।
इस अध्याय की मुख्य बातें
- कोरिलेशन मैट्रिक्स किन्हीं दो स्टॉक के बीच के कोरिलेशन को दिखाता है।
- स्टॉक A और स्टॉक B के बीच का कोरिलेशन वैसा ही होगा जैसा स्टॉक B और स्टॉक A के बीच का होगा।
- किसी स्टॉक का खुद से कोरिलेशन हमेशा 1 होता है।
- कोरिलेशन मैट्रिक्स के बाच की तिरछी रेखा (diagonal) किसी स्टॉक का खुद के साथ कोरिलेशन दिखाती है।
- कोरिलेशन मैट्रिक्स में तिरछी रेखा (diagonal) के ऊपर और नीचे एक जैसी संख्या दिखती है।










dhanywad lekin yeh samzna bhot hii mushkil hai ( khan ji koi aasan vidhi hai kya ho to krupya usee yehan par jod de)
इससे आसान आपको शायद कहीं भी यह नॉलेज उपलब्ध नहीं होगी, आप पढ़ते रहिये कुछ समझने में दिक्कत होतो यहाँ लिकेहिं हम आपको समझने की कोशिश करेंगे।
Waao…great and so much interesting explaination….. Thank u thanku so much
Happy Learning 🙂
I am preparing homework (on 5 stocks to find out portfolio variance) as you say in last lesson,
I have prepare all of things properly according to you and formula too,
But, in last step when i calculated correlation matrix,
then the correlation matrix of same stock (Ex- CIPLA & CIPLA) is not 1.
It is apporx 0.99 .
Plz, tell me where i am missing ??
Thats ok..if you increase the decimal places, it will read 0.9999, which is almost 1.
Got it, sir
And thanks.
मैं एक्सेल में फंक्शन का इस्तेमाल करके स्टॉक का वैरिंयस, कॉवैरियंस और कुरिलेशन निकाल लेता हूं सिर्फ डेली रिर्टन डाटा की जरूरत पड़ती है. तो क्या पोर्टफोलियो का वेरियंस निकालने के लिए ऐसा ही कुछ एक्सल फंक्शन नहीं है.
जी हाँ उपलध होगी आपको एक्सेल एक्स्प्लोर करना पड़ेगा।