4.1 – एक नजर फिर
इस अध्याय को शुरू करने के पहले एक नजर डाल लेते हैं कि अब तक हमने क्या-क्या चर्चा की है।
इस मॉड्यूल के शुरु में हमने चर्चा की थी कि बाजार में निवेश करने पर कारोबारियों के लिए दो तरीके के रिस्क होते हैं। वो जब भी कोई स्टॉक खरीदते हैं तो उन्हें सिस्टमैटिक रिस्क और अनसिस्टमैटिक रिस्क उठाना होता है। इन दोनों के अंतर को समझने के बाद हमने रिस्क को एक पोर्टफोलियो की नजर से समझा। पोर्टफोलियो रिस्क या पोर्टफोलियो वैरियंस से जुड़ी चर्चा के दौरान हमने 2 सिद्धांतों वैरियंस और कोवैरियंस को जाना। वैरियंस हमें यह बताता है कि किसी स्टॉक का रिटर्न उसके औसत रिटर्न से कितनी दूर तक जा सकता है। जबकि कोवैरियंस एक स्टॉक के रिटर्न और किसी दूसरे स्टॉक के रिटर्न के बीच के वैरियंस को बताता है। वैरियंस और कोवैरियंस पर यह चर्चा मुख्यत दो स्टॉक के पोर्टफोलियो के लिए की गई थी, लेकिन उस चर्चा को हमने समाप्त किया था एक आम पोर्टफोलियो से जिसमें आमतौर पर कई स्टॉक होते हैं। कई स्टॉक वाले पोर्टफोलियो के वैरियंस, कोवैरियंस और कोरिलेशन को निकालने के लिए हमें मैट्रिक्स अल्जेब्रा (Algebra/बीजगणित) की जरूरत पड़ेगी।
तो अब हम यही करेंगे।
इस अध्याय में हम बहुत सारे स्टॉक के लिए वैरियंस और कोवैरियंस का अनुमान लगाने पर चर्चा करेंगे। इस संदर्भ में हम मैट्रिक्स गुणन यानी मैट्रिक्स मल्टीप्लिकेशन (Matrix Multiplication) और दूसरे सिद्धांतों को भी देखेंगे। लेकिन आपको पता होना चाहिए कि ‘वैरियंस कोवैरियंस मैट्रिक्स’ से बहुत ज्यादा सूचना नहीं मिलती। इसमें से जरूरी सूचना निकालने के लिए हमें एक कोरिलेशन मैट्रिक्स भी बनाना पड़ता है। यह सब कर लेने के बाद हम कोरिलेशन मैट्रिक्स के नतीजों का इस्तेमाल करके पोर्टफोलियो वैरियंस निकालेंगे। याद रहे कि हमारा लक्ष्य पोर्टफोलियो वैरियंस निकालने का ही है। पोर्टफोलियो वैरियंस हमें यह बताता है कि अगर हमारे पोर्टफोलियो में काफी सारे स्टॉक हैं तो हम कितना रिस्क ले रहे हैं।
यहां आपको पता होना चाहिए कि अब हम पूरे पोर्टफोलियो के नजरिए से रिस्क को देख रहे हैं। इसके साथ ही, हम ऐसेट एलोकेशन पर भी चर्चा करेंगे और यह देखेंगे कि यह पोर्टफोलियो के रिटर्न और रिस्क पर किस तरह से असर डालता है। ऐसा करते हुए हम वैल्यू ऐट रिस्क (Value at Risk) के सिद्धांत पर भी नजर डालेंगे।
साथ ही हम ट्रेडर के नजरिए से भी रिस्क पर एक विस्तार से चर्चा करेंगे। ये जानेंगे कि ट्रेडिंग के दौरान वो किस तरीके से रिस्क को पहचान सकता है और कैसे उससे बच सकता है।
4.2 – वैरियंस कोवैरियंस मैट्रिक्स
मैं लगातार वैरियंस कोवैरियंस मैट्रिक्स के बारे में बात करता जा रहा हूं, तो आखिर यह वैरियंस कोवैरियंस मैट्रिक्स क्या होता है? यह एक वैरियंस मैट्रिक्स है या फिर एक कोवैरियंस मैट्रिक्स है? या फिर ये एक ही मैट्रिक्स है जिसका नाम है वैरियंस कोवैरियंस मैट्रिक्स।
वास्तव में यह एक ही मैट्रिक्स है जिसका नाम है वैरियंस कोवैरियंस मैट्रिक्स। अगर आपके पास 5 स्टॉक हैं तो आपको हर स्टॉक का वैरियंस पता होना चाहिए और साथ ही, आपको यह भी पता होना चाहिए कि उस एक स्टॉक और दूसरे बाकी बचे चार स्टॉक के बीच का कोवैरियंस कितना है। जब हम इसको एक उदाहरण से समझेंगे तो आपके लिए इसे समझना आसान हो जाएगा।
लेकिन यहां पर ध्यान दीजिए कि इसके लिए यह जरूरी है कि आपको मैट्रिक्स ऑपरेशन के बारे में कुछ आधारभूत जानकारी हो। अगर आपको मैट्रिक्स के बारे में कुछ भी नहीं पता है तो यहां हम खान एकेडमी का एक वीडियो दे रहे हैं जो मैट्रिक्स मल्टीप्लिकेशन को समझाता है – https://youtu.be/kT4Mp9EdVqs
अब हम कई स्टॉक वाले एक पोर्टफोलियो के लिए वैरियंस कोवैरियंस मैट्रिक्स की गणना करने और कोरिलेशन मैट्रिक्स बनाने की कोशिश करेंगे। एक अच्छा डायवर्सिफाइड पोर्टफोलियो वह होता है जिसमें 10 से 15 स्टॉक होते हैं। वैरियंस कोवैरियंस की गणना को समझाने के लिए मैं इस तरीके के पोर्टफोलियो का इस्तेमाल करना चाहता था लेकिन तब वह गणना इतनी लंबी हो जाती कि एक्सेल शीट में उसको समझाना मुश्किल हो जाता और वो किसी नए इंसान के लिए समझ के परे हो जाता। इसीलिए मैंने यहां पर सिर्फ 5 स्टॉक का पोर्टफोलियो लिया है। इस पोर्टफोलियो में जो 5 स्टॉक हैं, वो हैं
- सिपला
- आईडिया
- वंडरला– Wonderla
- PVR
- एल्केम
5 स्टॉक के पोर्टफोलियो के लिए वैरियंस कोवैरियंस मैट्रिक्स का आकार 5x5 होगा मतलब अगर किसी पोर्टफोलियो में स्टॉक की संख्या K है तो वैरियंस कोवैरियंस मैट्रिक्स का आकार K x K होगा।
वैरियंस कोवैरियंस मैट्रिक्स निकालने का फार्मूला यह है –
जहां,
k = पोर्टफोलियो में स्टॉक की संख्या
n = लिए गए आंकड़ों की संख्या
X = ये n x k का एक्सेस रिटर्न मैट्रिक्स है, इसे हम अभी आगे समझेंगे।
XT = X का ट्रांसपोज मैट्रिक्स
देखते हैं कि इस फार्मूले में होता क्या है, यह बात आपको अच्छे से तब समझ में आएगी जब हम इसका इस्तेमाल करेंगे।
सबसे पहले हम n x k का एक्सेस रिटर्न मैट्रिक्स निकालते हैं, फिर इस मैट्रिक्स को इसके अपने ट्रांसपोज मेट्रिक से गुणा करेंगे। यह एक मैट्रिक्स मल्टीप्लीकेशन होगा और इसके बाद जो मैट्रिक्स मिलेगा वह K x K मैट्रिक्स होगा। फिर हम इस K x K मैट्रिक्स के हर हिस्से को n से विभाजित करेंगे। जहां पर n देखे गए डेटा बिन्दुओं की संख्या है। इस विभाजन के बाद जो मैट्रिक्स मिलेगा वह एक K x K वैरियंस कोवैरियंस मैट्रिक्स होगा।
K x K वैरियंस कोवैरियंस मैट्रिक्स निकालने के बाद हम अपने अंतिम पड़ाव यानी कोरिलेशन मैट्रिक्स से सिर्फ एक कदम दूर रह जाते हैं।
आइए अब इस फार्मूले का इस्तेमाल करते हैं और ऊपर बताए गए 5 स्टॉक के लिए वैरियंस कोवैरियंस मैट्रिक्स निकालते हैं। इसके लिए हम माइक्रोसॉफ्ट एक्सेल का इस्तेमाल करेंगे। मैंने इन सभी पांच स्टॉक के लिए पिछले 6 महीने की हर दिन की क्लोजिंग कीमत निकाली हुई है।
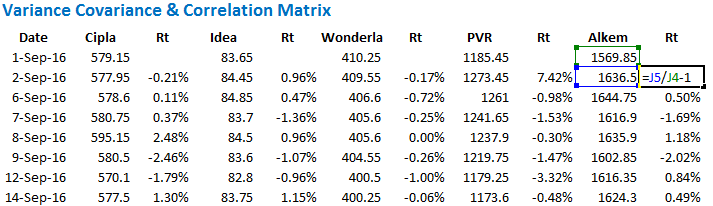
कदम 1 – पहले डेली यानी दैनिक रिटर्न निकाल लें। इसे तो अब तक आप समझ चुके होंगे इसलिए मैं इसको निकालने का तरीका यहां नहीं बता रहा हूं। बस एक्सेल शीट का एक चित्र दे रहा हूं
जैसा कि आप देख सकते हैं कि मैंने स्टॉक की क्लोजिंग कीमत के बगल में ही उसका डेली रिटर्न निकाल कर लिखा है, रिटर्न निकालने का फार्मूला भी साथ में दिखाया गया है।
कदम 2 – हर स्टॉक का औसत डेली रिटर्न निकालें। इसके लिए आप एक्सेल के एवरेज फंक्शन का इस्तेमाल कर सकते हैं।
कदम 3 – एक्सेस रिटर्न मैट्रिक्स बनाएं।
एक्सेस रिटर्न मैट्रिक्स यह बताता है कि स्टॉक के दैनिक यानी डेली रिटर्न और औसत रिटर्न में कितना अंतर है। हम ने इसको पिछले अध्याय में भी निकाला था जब हम दो स्टॉक के बीच में वैरियंस निकाल रहे थे।
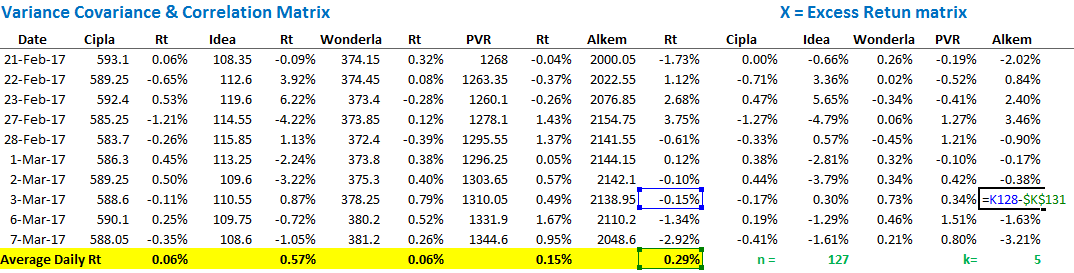
मैंने एक्सेस रिटर्न मैट्रिक्स इस तरह से बनाया है।
यहां ध्यान दीजिए कि यह मैट्रिक्स n x k आकार का है, जहां पर n हमें यह बता रहा है कि कितनी बार आंकड़ों को लिया गया है (यहां 127 बार) और k हमें बता रहा है कि कितने स्टॉक हैं (यहां पर 5) तो यहां पर हमारा मैट्रिक्स 127 x 5 बना है। हमने इस मैट्रिक्स को नाम दिया है- X
कदम 4 – अब XT X मैट्रिक्स ऑपरेशन करना है जिससे k x k मैट्रिक्स बन जाए।
यह सुनने में काफी हाई फाई लग रहा होगा लेकिन ऐसा नहीं है।
XT एक नया मैट्रिक्स है, जिसे X मैट्रिक्स के रो (row) और कॉलम (column) को आपस में अदल बदल करके बनाया गया है और अब इसे X का ट्रांसपोज मैट्रिक्स कहा जाएगा और इसे दिखाने के लिए XT सिंबल का इस्तेमाल किया जाएगा। हमारा लक्ष्य है X को उसके ट्रांसपोज मैट्रिक्स से गुणा करना यानी XT X मैट्रिक्स बनाना।
याद रखिए कि इस तरह से जो मैट्रिक्स बनेगी वो k x k मैट्रिक्स होगी, जहां K, उस मैट्रिक्स में मौजूद स्टॉक की संख्या बता रहा है। हमारे इस उदाहरण में ये 5 x 5 का मैट्रिक्स होगा।
हम एक्सेल में इसे एक बार में कर सकते हैं। मैं k x k मैट्रिक्स बनाने के लिए निम्न कदम उठाऊंगा।
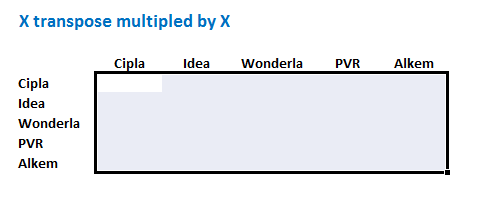
स्टॉक को रो और कॉलम में लिख लें
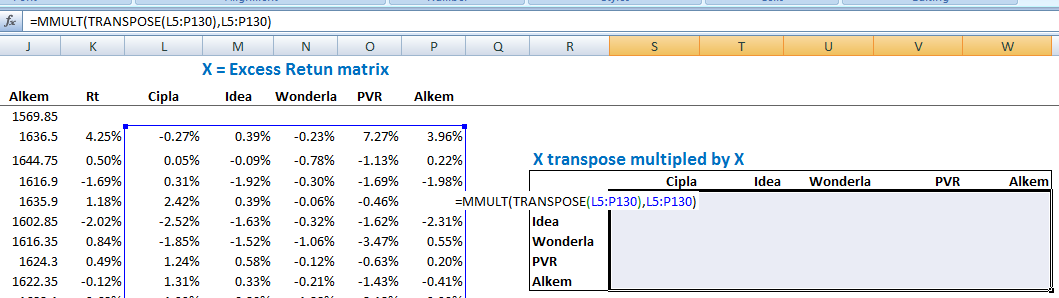
अब फंक्शन = MMULT (transposeX),X), याद रहे कि X का मतलब है एक्सेस रिटर्न मैट्रिक्स।
याद रखें कि इस फॉर्मूले का इस्तेमाल करते समय आपको k x k को हाईलाइट करना है। फॉर्मूला टाइप करने के बाद आपको सीधे ENTER नहीं दबाना है। आपको Ctrl+Shift+Enter दबाना है। वास्तव में एक्सेल में हर ऐसे फंक्शन के लिए Ctrl+Shift+Enter ही दबाना है।
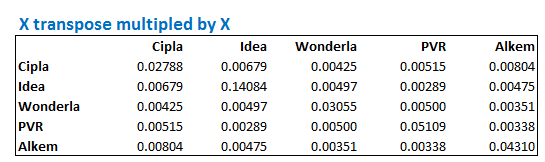
जब आप Ctrl+Shift+Enter दबाएंगे तो एक्सेल आपके सामने k x k मैट्रिक्स पेश कर देगा, जो ऐसा दिखेगा
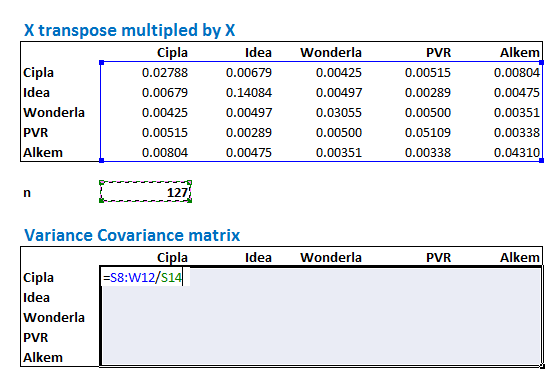
कदम 5 – वैरियंस कोवैरियंस मैट्रिक्स के पहले का ये अंतिम कदम है। अब हमें XT X मैट्रिक्स के पूरे हिस्से को डेटा बिन्दुओं की संख्या यानी n से विभाजित करना है। मैं वैरियंस कोवैरियंस मैट्रिक्स का फार्मूला फिर से दे रहा हूं
अब हम फिर से k x k मैट्रिक्स का लेआउट लाएंगे
जब ये लेआउट आ जाए तो सेल (cells) को डी सेलेक्ट (deselect) किए बगैर पूरे XT X मैट्रिक्स को सेलेक्ट करना है और फिर उसे n से यानी 127 से विभाजित करना है। ध्यान रहे कि ये अभी भी ऐरे (Array) फंक्शन है इसलिए यहां पर Ctrl+Shift+Enter दबाना है सिर्फ Enter नहीं दबाना है।
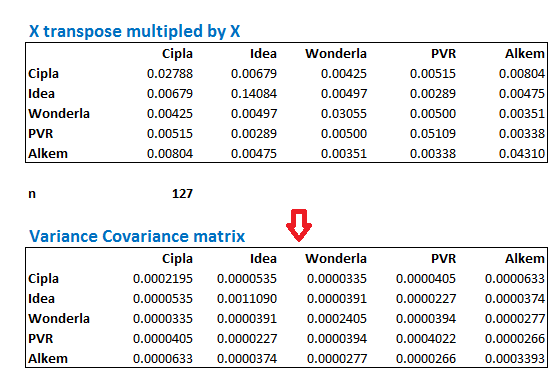
जब आप Ctrl+Shift+Enter दबाएंगे तो आपको वैरियंस कोवैरियंस मैट्रिक्स मिलेगा। आपको दिखेगा कि इसमें संख्याएं काफी छोटी हैं, लेकिन अभी आप उसकी चिन्ता ना करें। तो ये रहा वैरियंस कोवैरियंस मैट्रिक्स –
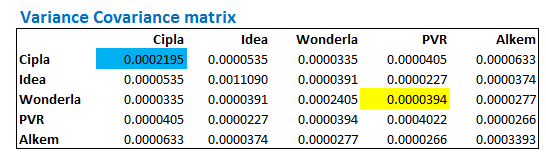
अब वैरियंस कोवैरियंस मैट्रिक्स को जरा आराम से समझने की कोशिश करते हैं। मान लीजिए मुझे दो स्टॉक्स के बीच में कोवैरियंस को जानना है, उदाहरण के तौर पर वंडरला और PVR के बीच। तो मुझे करना सिर्फ यह है कि अपने बाएं तरफ वाले कॉलम में मुझे वंडरला को खोजना है और उसी रो में हमें PVR को तलाशना है। उनके सामने जो संख्या लिखी है वह इन दोनों के बीच का कोवैरियंस होगा। मैंने इसको यहां पीले रंग से हाईलाइट किया है।
तो मैट्रिक्स हमें बता रहा है कि वंडरला और PVR के बीच कोवैरियंस 0.000034 है। ध्यान रहे कि PVR और वंडरला के बीच में भी कोवैरियंस यही होगा।
अब उस संख्या पर नजर डालिए जिसको मैंने नीले रंग से हाईलाइट किया है यह संख्या सिप्ला और सिप्ला को दिखाती है, इसका क्या मतलब हुआ? मतलब यह सिप्ला और सिप्ला के बीच का कोवैरियंस है। ध्यान दें कि स्टॉक का कोवैरियंस और कुछ नहीं उस स्टॉक का वैरियंस ही होता है। इसी वजह से इस मैट्रिक्स को वैरियंस कोवैरियंस मैट्रिक्स कहते हैं क्योंकि यह हमें दोनों आंकड़े देता है।
लेकिन कड़वी बात यह है कि वैरियंस कोवैरीयंस मैट्रिक्स अपने आप में कुछ ज्यादा काम की चीज नहीं है। जैसा कि आप खुद ही देख सकते हैं कि यह संख्याएं काफी छोटी हैं और इनसे कोई मतलब निकालना मुश्किल काम है। इसीलिए हमें कोरिलेशन मैट्रिक्स की जरूरत पड़ती है।
अगले अध्याय में हम कोरिलेशन मैट्रिक्स बनाने और उसको समझने की कोशिश करेंगे। जिसके जरिए हम पोर्टफोलियो का वैरीयंस निकालेंगे जो कि हमारा लक्ष्य है। हम यह अध्याय खत्म करें इसके पहले आपके लिए कुछ अभ्यास देता हूं
- 5 या उससे ज्यादा स्टॉक का एक साल का डेटा डाउनलोड कीजिए
- उसका वैरियंस कोवैरियंस मैट्रिक्स निकालिए
- किसी एक स्टॉक का वैरियंस निकालिए, फिर एक्सेल में = ‘Var()’ फंक्शन का इस्तेमाल करके उसका वैरियंस निकालिए और देखिए कि दोनों आंकड़े एक जैसे हैं या नहीं है।
आप इस एक्सेलशीट को यहां पर डाउनलोड कर सकते हैं
इस अध्याय की मुख्य बातें
- X का मतलब है एक्सेस रिटर्न मैट्रिक्स
- एक्सेस रिटर्न मैट्रिक्स किसी टाइम सीरीज पर किसी स्टॉक के डेली रिटर्न और उसके औसत रिटर्न का अंतर है।
- ट्रांसपोज मैट्रिक्स को दिखाने के लिए XT का इस्तेमाल किया जाता है।
- डेटा बिन्दुओं की संख्या को n दिखाता है। उदाहरण के लिए n यहां 127 है, एक साल के लिए ये 252 होगा।
- एक्सेस रिटर्न मैट्रिक्स का आकार n x k होता है, यहां पर k हमें बता रहा है कि इसमें कितने स्टॉक हैं
- जब हम XT X मैट्रिक्स के पूरे हिस्से को डेटा बिन्दुओं की संख्या यानी n से विभाजित करते हैं तो हमें वैरियंस कोवैरियंस मैट्रिक्स मिलता है
- वैरियंस कोवैरियंस मैट्रिक्स का आकार k x k का होता है।
- किसी स्टॉक का उसके साथ कोवैरियंस और कुछ नहीं, उस स्टॉक का वैरियंस ही होता है
- वैरियंस कोवैरियंस मैट्रिक्स हमें कोरिलेशन मैट्रिक्स तक ले जाता है






What is the formula for find out the variance of stock?
Dear Mam,
No excel sheet link found
Thank you, we will check and add this.
tqsm team zerodha
आपका अभिनन्दन है।