21.1 – पृष्ठभूमि

इस मॉड्यूल में अब तक हमने सभी महत्वपूर्ण ऑप्शन ग्रीक के बारे में बात कर ली है और उनके उपयोग को भी समझ लिया है। अब समय है, यह समझने का कि इन ग्रीक की गणना कैसे की जाती है। ब्लैक एंड स्कोल्स (B&S) ऑप्शन प्राइसिंग कैलकुलेटर, ब्लैक एंड स्कोल्स ऑप्शन प्राइसिंग मॉडल (Black and Scholes options pricing model) पर आधारित है जिसे पहली बार फिशर ब्लैक और मायरॉन स्कोल्स ( Fisher Black and Myron Scholes) ने 1973 में बनाया था, हालांकि बाद में रॉबर्ट सी मर्टन (Robert C Merton) ने इस मॉडल को विकसित किया और इसको पूरी तरीके से गणित पर आधारित पर एक फार्मूले का रूप दिया। 

वित्तीय बाजारों में इस प्राइसिंग मॉडल को काफी महत्व दिया जाता है। वास्तव में रॉबर्ट सी मर्टन को और मायरॉन स्कोल्स को 1997 में इकोनॉमिक्स का नोबेल नोबेल प्राइज भी मिला। B&S प्राइसिंग मॉडल में गणित के कई सिद्धांत जैसे पार्शियल डिफरेंशियल इक्वेशन(Partial Differential equation), नॉरमल डिसटीब्यूशन (Normal Distribution), स्टेास्टिक प्रोसेसेस (Stochastic Processes) आदि का इस्तेमाल किया जाता है। इस मॉड्यूल में हम आपको गणित के बारे में नहीं पढ़ाने वाले हैं बल्कि हमारा उद्देश्य है कि आप इस फार्मूले के उपयोग को ठीक ढंग से समझ सकें। लेकिन फिर भी आप इस मॉडल को समझने के लिए खान एकेडमी के इस वीडियो को देख सकते हैं

 https://youtu.be/pr-u4LCFYEY

21.2 – क्या है ये मॉडल

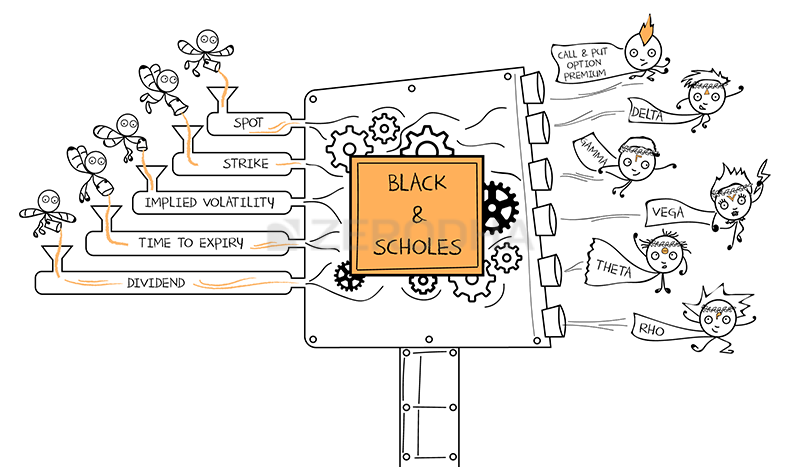
B&S कैलकुलेटर को आप एक ऐसी मशीन मान सकते हैं, जिसमें बहुत सारी चीजें डालने पर आपको कई तरह की चीजें बनकर मिलती हैं। जो चीजें इसमें डाली जाती है वह वास्तव में मार्केट से जुड़े हुए आंकड़े होते हैं और जो चीजें निकलती हैं वह ऑप्शन ग्रीक्स होते हैं। 

यह मॉडल इस तरह से काम करता है- 

1. हम इस मॉडल में स्पॉट कीमत, स्ट्राइक कीमत, ब्याज दर, इंप्लाइड वोलैटिलिटी, डिविडेंड और एक्सपायरी में बचे हुए दिन जैसे आंकड़े डालते हैं। 
2. प्राइसिंग मॉडल इन पर गणित के फार्मूले का इस्तेमाल करता है और उसके बाद अपने नतीजे देता है। 
3. इन नतीजों में ऑप्शन ग्रीक तथा कॉल और पुट ऑप्शन की सैद्धांतिक कीमतें निकलती है। 

आप इसे नीचे के चित्र से ठीक ढंग से समझ सकते हैं-

इस मॉडल में जिन चीजों को डालना पड़ता है- 

स्पॉट कीमत-  यह वह कीमत है जिस कीमत पर अंडरलाइंग स्पॉट बाजार में बिक रहा है। याद रखिए कि हम चाहें तो यहां पर स्पॉट कीमत की जगह फ्यूचर कीमत भी डाल सकते हैं। जब ऑप्शन कॉन्ट्रैक्ट फ्यूचर की कीमत को अंडरलाइंग के तौर पर इस्तेमाल कर रहा हो तो ऐसा किया जाता है। कमोडिटी फ्यूचर्स और करेंसी ऑप्शन में कई बार फ्यूचर कीमत को अंडरलाइंग के तौर पर इस्तेमाल किया जाता है। वैसे इक्विटी बाजार में ऑप्शन कॉन्ट्रैक्ट हमेशा स्पॉट की कीमत पर ही आधारित होते हैं। 

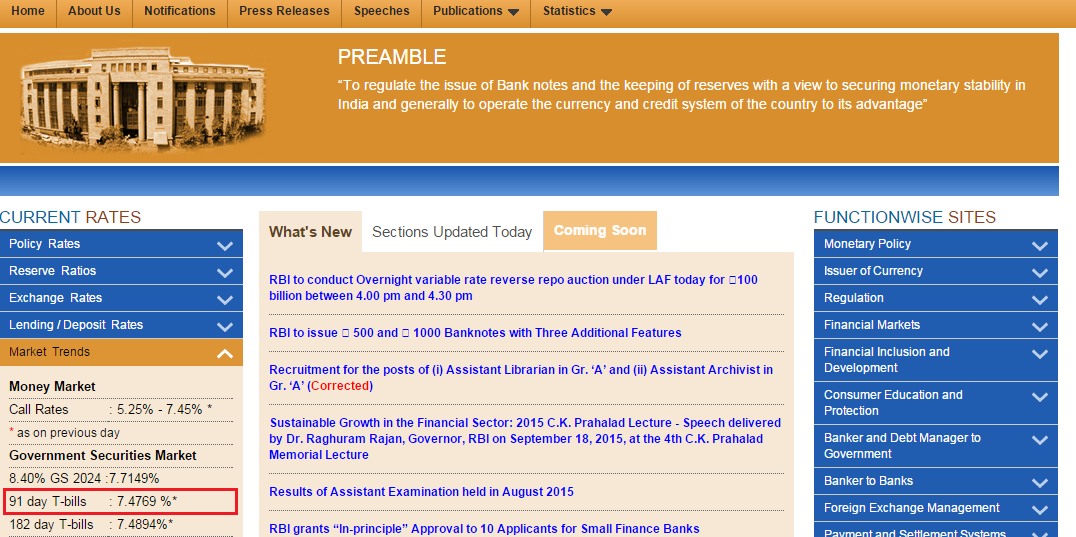
ब्याज दरें- यह ब्याज की वो रिस्क फ्री दर है जो अर्थव्यवस्था में मिल रही है। इसके लिए आप RBI के 91 डे (91 day) के ट्रेजरी बिल के दर का इस्तेमाल कर सकते हैं। यह दर आपको RBI की वेबसाइट से मिल सकती है। RBI ने यह रेट अपने लैंडिंग पेज पर भी डाला है, जिसको नीचे हाईलाइट किया गया है। 

सितंबर 2015 में यह रेट 7.4769% है। 

डिविडेंड– यह प्रति शेयर मिलने वाला वह डिविडेंड है जिसकी उम्मीद की जा रही है। इसका इस्तेमाल तब होता है जब इस एक्सपायरी के दौरान स्टॉक एक्स डिविडेंड (ex-dividend) होने वाला हो। उदाहरण के तौर पर, मान लीजिए कि आज 11 सितंबर है और आप ICICI बैंक के ऑप्शन कान्ट्रैक्ट के लिए ऑप्शन ग्रीक की गणना करना चाहते हैं और ICICI बैंक 18 सितंबर को एक्स डिविडेंड (ex-dividend)  हो रहा है। इस पर ₹4 डिविडेंड मिलने वाला है। सितंबर सीरीज की एक्सपायरी 24 सितंबर 2015 को है इसलिए यहां पर इस गणना के लिए डिविडेंड ₹4 होगा।

एक्सपायरी में बचे हुए दिन– एक्सपायरी में कितने दिन बचे हुए हैं। 

वोलैटिलिटी– यहां पर आपको ऑप्शन की इंप्लाइड वोलैटिलिटी का इस्तेमाल करना होगा। NSE की तरफ से जारी किए गए ऑप्शन चेन में आपको सभी ऑप्शन कॉन्ट्रैक्ट की इंप्लायड वोलैटिलिटी का डेटा मिल सकता है। उदाहरण के तौर पर, नीचे के चित्र में ICICI बैंक के 280 CE को दिखाया गया है और हम देख सकते हैं कि इसका IV 43.55% है।

आइए अब इन आंकड़ों का इस्तेमाल करके ICICI के 280 कॉल ऑप्शन के ग्रीक को निकालते हैं– 

• स्पॉट कीमत = 272.7 
• ब्याज दर (इंटरेस्ट रेट) = 7.4769% 
• डिविडेंड = 0 
• एक्सपायरी में बचे हुए दिन = 1 (एक आज 23 सितंबर है और एक्सपायरी 24 सितंबर को है) 
• वोलैटिलिटी = 43.55% 

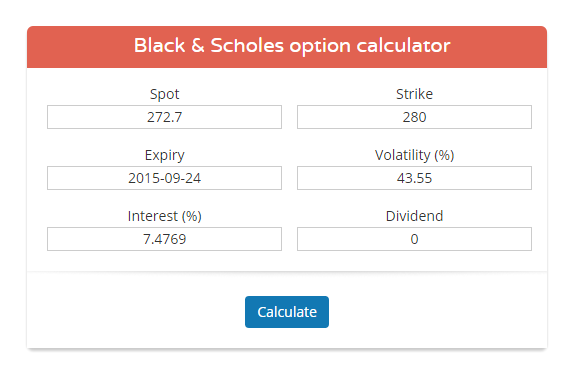
अब जब हमारे पास यह सारी जानकारी है तो हम इसको ब्लैक एंड स्कोल्स ऑप्शन केलकुलेटर में डालेंगे। यह केलकुलेटर हमारी वेबसाइट पर मौजूद है- https://zerodha.com/tools/black-scholes आप इसका इस्तेमाल करके ऑप्शन ग्रीक्स निकाल सकते हैं। 

एक बार जब आप जरूरी डेटा डाल देते हैं और कैलकुलेट का बटन दबाते हैं, तो कैलकुलेटर आपको ऑप्शन ग्रीक का मूल्य बता देता है।

इससे जो चीजें निकलती हैं 

• 280 के कॉल ऑप्शन और 280  पुट ऑप्शन का प्रीमियम। यह एक सैद्धांतिक ऑप्शन कीमत है जो कि इस ऑप्शन कैलकुलेटर ने निकाली है। लेकिन वास्तव में यह बाजार की मौजूदा ऑप्शन कीमत के बराबर होनी चाहिए। 
• प्रीमियम की कीमत के नीचे, सभी ऑप्शन ग्रीक को दिखाया गया है। 

मुझे उम्मीद है कि अब तक आप हर ऑप्शन ग्रीक्स के बारे में समझ चुके हैं और यह जानते हैं कि वह क्या बता रहे हैं और इनका इस्तेमाल आप कैसे कर सकते हैं। 

ऑप्शन कैलकुलेटर के बारे में एक और बात जो आपको जानना चाहिए वह यह है कि ऑप्शन कैलकुलेटर का इस्तेमाल मुख्य तौर पर ऑप्शन ग्रीक्स को निकालने के लिए और ऑप्शन की सैद्धांतिक कीमत को निकालने के लिए किया जाता है। कभी-कभी आंकड़े डालते हुए थोड़े से फेरबदल की वजह से आपको कुछ अंतर मिल सकता है, इसलिए जरूरी है कि आप अपने अनुमानों में मॉडलिंग के लिए थोड़ी जगह रखें। लेकिन कुल मिलाकर ऑप्शन कैलकुलेटर काफी सही गणना करता है।

21.3 – पुट कॉल पैरिटी (Put Call Parity)

हम यहां पर ऑप्शन प्राइसिंग के मुद्दे पर बात कर रहे हैं इसलिए शायद यहीं पर हमें पुट कॉल पैरिटी (Put Call Parity) यानी PCP पर बात कर लेनी चाहिए। पुट कॉल पैरिटी एक सीधा-साधा गणित का समीकरण है जो कि बताता है-

पुट कीमत + स्पॉट कीमत + स्ट्राइक की मौजूदा कीमत (मैच्योरिटी तक निवेश पर) + कॉल की कीमत 

Put Value + Spot Price = Present value of strike (invested to maturity) + Call Value.

यह समीकरण बिल्कुल सही साबित होता है अगर –

1. पुट और कॉल दोनों ऑप्शन एटीएम हैं 
2. ऑप्शन यूरोपीयन है 
3. दोनों एक साथ ही एक्सपायर हो रहे हैं 
4. ऑप्शंस को एक्सपायरी तक होल्ड किया जा रहा है 

जो लोग प्रेजेंट वैल्यू के बारे में नहीं जानते हैं मेरी उनको सलाह है कि वह इसको पढ़ें – http://zerodha.com/varsity/chapter/dcf-primer/ 

लेकिन अगर आप प्रेजेंट वैल्यू के सिद्धांत को समझते हैं तो आप इस समीकरण को ऐसे भी देख सकते हैं 

P + S = Ke(-rt) + C

जहां पर यह Ke(-rt)  स्ट्राइक की प्रेजेंट वैल्यू को बताता है जबकि  K  स्ट्राइक कीमत है। गणित के नजर से देखें तो स्ट्राइक K लगातार डिस्काउंट हो रहा है ‘r’ ओवर ‘टाइम की ‘t’ (‘r’ over time ‘t’ ) की दर से। 

यह भी समझ लीजिए कि अगर आप स्ट्राइक की प्रेजेंट वैल्यू को मैच्योरिटी तक होल्ड करते हैं तो आपको स्ट्राइक कीमत ही वापस मिल जाएगी। इसलिए इस समीकरण को इस तरीके से भी दिखाया जा सकता है 

पुट ऑप्शन +  स्पॉट कीमत = स्ट्राइक कीमत + कॉल ऑप्शन

Put Option + Spot Price = Strike + Call options 

तो यह दोनों बराबर क्यों होने चाहिए? इसको अच्छे तरीके से समझने के लिए आप मान लीजिए कि दो ट्रेडर हैं A और B

• ट्रेडर A, ATM पुट ऑप्शन को होल्ड करता है और अंडरलाइंग स्टॉक के 1 शेयर को अपने पास रखता है। (PCP समीकरण के बाएं तरफ का हिस्सा) 
• ट्रेडर B, कॉल ऑप्शन को होल्ड करता है और स्ट्राइक कीमत के बराबर का कैश या नकद (PCP समीकरण का दायीं तरफ का हिस्सा)

ऊपर के तथ्यों के आधार पर PCP बताता है कि दोनों ट्रेडर एक बराबर पैसे कमाएंगे (अगर वह अपनी पोजीशन को एक्सपायरी तक होल्ड करते हैं)। यहां पर कुछ आंकड़े नंबर डालकर देखते हैं कि यह समीकरण कितना सही है-

अंडरलाइंग = इंफोसिस 

स्ट्राइक = 1200 

स्पॉट कीमत = 1200 

ट्रेडर A होल्ड करता है = 1200 PE + इंफोसिस का एक शेयर 1200 पर 

ट्रेडर B होल्ड करता है = 1200 CE + स्ट्राइक के बराबर का नकद यानी 1200 

अब मान लीजिए की एक्सपायरी पर इंफोसिस 1100 पर एक्सपायर होता है, तो क्या होगा? 

ट्रेडर A  का पुट ऑप्शन मुनाफा देता है और वह ₹100 कमाता है। लेकिन उसके पास जो एक शेयर है वहां पर वह ₹100 का नुकसान करता है। इसलिए कुल मिलाकर उसके पास जो रकम बचती है वह है 100 + 1100  = 1200

ट्रेडर B का कॉल ऑप्शन बिना कीमत का यानी वर्थलेस (worthless) हो जाता है। इसलिए उसके ऑप्शन की कीमत 0 पहुंच जाती है। लेकिन उसके पास  ₹1200 हैं, इसलिए उसके पास कुल बची हुए रकम है 0 + 1100 = 1200  

अब एक और उदाहरण लेते हैं। मान लीजिए कि एक्सपायरी पर इंफोसिस 1350 पर पहुंच जाता है। तो अब इन दोनों ट्रेडर के लिए यह आंकड़ा कैसे बदलता है- 

ट्रेडर A =  पुट ऑप्शन जीरो हो जाता है, उसका शेयर 1350 पर पहुंच जाता है 

ट्रेडर  B =  कॉल की वैल्यू यानी कीमत ₹150 बढ़ जाती है, और उसके पास नकद है ₹1200 तो कुल रकम हुई 1350 

तो इस तरह से स्टॉक कहीं पर भी एक्सपायर हो, यह समीकरण सही साबित होता है। यानी ट्रेडर A और ट्रेडर B दोनों एक बराबर पैसे कमाते हैं। अब आप PCP का इस्तेमाल करके एक ट्रेडिंग स्ट्रेटजी कैसे बनाएंगे? इसके लिए आपको अगले मॉड्यूल का इंतजार करना होगा, जिसमें हम ऑप्शन स्ट्रेटजी की बात करेंगे। लेकिन उसके पहले इस मॉड्यूल में अभी दो और अध्याय बाकी हैं।

इस अध्याय की मुख्य बातें 

1. ऑप्शनन कैलकुलेटर ब्लैक एंड स्कोल्स मॉडल पर आधारित है। 
2. ब्लैक एंड स्कोल्स मॉडल का इस्तेमाल करके ऑप्शन के सैद्धांतिक कीमतें और ऑप्शन ग्रीक्स को पता किया जा सकता है।
3. कैलकुलेटर में इंटरेस्ट रेट यानी ब्याज दरें वह होती है जो RBI की  वेबसाइट पर रिस्क फ्री  रेट के तौर पर दिखाई जाती हैं।
4. इंप्लाइड वोलैटिलिटी का आंकड़ा NSE की वेबसाइट पर दिए गए ऑप्शन चेन में से निकाला जा सकता है।
5. पुट कॉल पैरिटी बताता है कि पुट ऑप्शन और स्पॉट का जोड़, कॉल ऑप्शन प्लस स्ट्राइक के बराबर होता है।