7.1 – संभावित रिटर्न / एक्सपेक्टेड रिटर्न्स

जिन लोगों ने कभी पोर्टफोलियो तकनीक का इस्तेमाल नहीं किया है उनके लिए अगले 2 अध्याय बहुत काम के साबित होने वाले हैं। इन अध्यायों में हम बात करेंगे पोर्टफोलियो से कितना रिटर्न मिल सकता है यानी एक्सपेक्टेड रिटर्न की और इसके आधार पर पोर्टफोलियो में सुधार कैसे किया जाए। इसे पोर्टफोलियो ऑप्टिमाइजेशन (Portfolio Optimization) कहते हैं (इस पर हम अगले अध्याय में चर्चा करेंगे) इसके जरिए आपको यह पता चलता है कि किसी एक स्टॉक में कितने पैसे लगाने चाहिए जिससे आपको सबसे ज्यादा रिटर्न मिले और रिस्क और रिटर्न का संतुलन भी बना रहे। आमतौर पर फाइनेंस से जुड़े लोग इन मुद्दों पर चर्चा नहीं करते और यह जानकारी अपने तक ही सीमित रखते हैं। लेकिन हम यह जानकारी आप तक पहुंचा रहे हैं। 

लेकिन ध्यान रहे कि इसको अच्छे से समझने के लिए यह जरूरी है कि अब तक पिछले कुछ अध्यायों में हमने जिन विषयों पर बात की है आप उनके बारे में जानते हों। इसलिए अगर आपने अब तक उन अध्यायों को नहीं पढ़ा है तो मेरी सलाह यह होगी कि आप पहले जाकर उनको पढ़ लेँ। उन पर बिताए गए कुछ घंटे आपके लिए बाजार में पैसे कमाने में काफी काम आने वाले हैं। यहां पर भी हम उसी एक्सेल शीट का इस्तेमाल करेंगे जिसका इस्तेमाल हमने पिछले कुछ अध्यायों में किया है। 

तो आइए शुरू करते हैं – 

शुरुआत के लिए सबसे पहले हम पोर्टफोलियो वैरियंस पर नजर डालते हैं जिसको हमने पिछले अध्याय में निकाला था

इस संख्या से हमें पता चलता है कि पोर्टफोलियो से कितना रिस्क जुड़ा हुआ है। याद रखें कि हमने वैरियंस निकालन् के लिए डेली यानी दैनिक डेटा का इस्तेमाल किया था, इसलिए 1.11%  हर दिन के रिस्क को बताता है। 

रिस्क, वैरियंस या वोलैटिलिटी सब एक सिक्के की तरह हैं जिसका एक दूसरा पहलू भी है। जिस कीमत पर हम निवेश करते हैं, उससे नीचे की तरफ का कोई भी चाल हमारे लिए रिस्क होता है लेकिन जब वही चाल दूसरी तरफ यानी हमारे निवेश की कीमत से ऊपर की तरफ होती है तो उसको रिटर्न कहते हैं। हम वैरियंस के डेटा का इस्तेमाल करके यह जानने की कोशिश करेंगे कि एक साल में हमारे पोर्टफोलियो किस रेंज (दायरे) में बदलाव हो सकता है। अगर आपने ऑप्शन का मॉड्यूल पढ़ा है तो आपको समझ में आ गया होगा कि मैं क्या बात कर रहा हूं। 

लेकिन ऐसा करने के पहले हमें पोर्टफोलियो के एक्सपेक्टेड रिटर्न को पता करना होगा। पोर्टफोलियो का एक्सपेक्टेड रिटर्न निकालने के लिए हमें उसमें के हर स्टॉक के औसत रिटर्न को उसके अपने वेट (वजन/weight) से गुणा करना होगा और फिर इन सबका जोड़ निकालना होगा। फिर इस मिली हुई संख्या को 252 (साल में ट्रेडिंग वाले दिनों की संख्या) से गुणा करना होगा। सीधे शब्दों में कहें तो हम अपने दैनिक यानी डेली रिटर्न को वार्षिक रिटर्न में बदल रहे हैं और फिर इसको अपने निवेश के हिसाब से निकाल रहे हैं। 

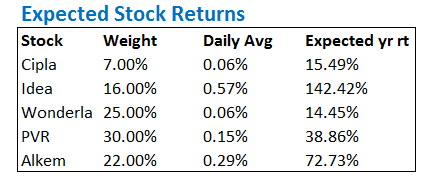
तो आइए देखते हैं कि जो हमारा पोर्टफोलियो है उसका एक्सपेक्टेड रिटर्न कितना है। उम्मीद है कि इसको देखने के बाद आपको यह बात अच्छे से समझ में आएगी। नीचे के चार्ट में मैंने डेटा को कैसे लगाया है देखिए –

पहले 3 कॉलम तो आसानी से समझ में आ जाएंगे, अंतिम कॉलम में मैंने हर दिन के औसत रिटर्न को 252 से गुणा किया है जिससे कि उस स्टॉक का वार्षिक रिटर्न पता चल सके। 

उदाहरण के लिए सिप्ला में – 0.06% * 252 = 15.49%

इसको समझना बहुत आसान है, मान लीजिए कि मैंने अपने सारे पैसे सिप्ला में लगाए होते और किसी दूसरे स्टॉक में नहीं, तो पोर्टफोलियो में सिप्ला का वेट यानी वजन होता 100% और इससे मैं 15.49% के रिटर्न की उम्मीद करता। लेकिन चूंकि मैंने सिप्ला में अपनी कुल पूंजी का सिर्फ 7% ही लगाया है इसलिए सिप्ला से मेरा एक्सपेक्टेड रिटर्न होगा –

वजन (वेट/weight) * एक्सपेक्टेड रिटर्न

= 7% * 15.49%

= 1.08%

तो इसी तरह से हम अब पोर्टफोलियो का एक्सपेक्टेड रिटर्न भी निकाल सकते हैं – 

जहां,

Wt = हर स्टॉक का वजन

Rt = स्टॉक का एक्सपेक्टेड वार्षिक रिटर्न

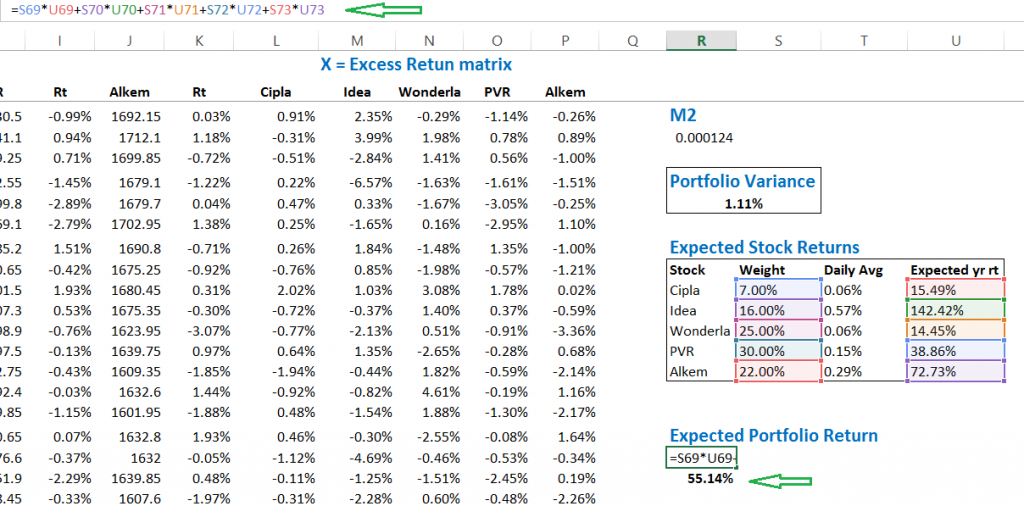
मैंने इसी फार्मूले का इस्तेमाल अपने पोर्टफोलियो के 5 स्टॉक पर किया और ये है उसका परिणाम –

तो अब हमें दो ऐसे मापदण्ड मिल गए हैं जो पोर्टफोलियो के हिसाब से बहुत ही ज्यादा महत्वपूर्ण हैं। वो हैं, पोर्टफोलियो का एक्सपेक्टेड रिटर्न जो कि 55.4% है और पोर्टफोलियो का वैरियंस जो कि 1.11% है। 

हम अगर चाहे तो पोर्टफोलियो के इसी वैरियंस से इसका वार्षिक वैरियंस भी निकाल सकते हैं, इसके लिए हमें सिर्फ इसको 252 के वर्गमूल (Square root) से गुणा करना होगा –

वार्षिक वैरियंस =

 

= 1.11% * Sqrt (252)

= 17.64%

अभी के लिए हम इन आंकड़ों को अलग रखते हैं।

अब हमें नॉर्मल डिस्ट्रीब्यूशन की चर्चा पर वापस लौटना होगा जिसे हमने ऑप्शन के मॉड्यूल में किया था। 

मेरी सलाह यह होगी कि आप जल्दी से डाल्टन बोर्ड एक्सपेरिमेंट (Dalton board experiment) के बारे में पढ़ लें और नॉर्मल डिस्ट्रीब्यूशन को समझ लें। साथ ही, यह भी जान लें कि इसका इस्तेमाल करके भविष्य के परिणाम का अनुमान कैसे लगाया जा सकता है। यहां पर, नॉर्मल डिस्ट्रीब्यूशन और इसके गुणों को जानना बहुत जरूरी है। 

पोर्टफोलियो का रिटर्न आमतौर पर नॉर्मल डिस्ट्रीब्यूशन तरीके से ही होता है। अगर आप किसी पोर्टफोलियो के डिस्ट्रीब्यूशन को ग्राफ पर प्लॉट करेंगे तो आपको एक नॉर्मल डिस्ट्रीब्यूशन वाला पोर्टफोलियो मिलेगा। एक पोर्टफोलियो का नॉर्मल डिस्ट्रीब्यूशन मिल जाए तो उसके आधार पर पोर्टफोलियो के अगले 1 साल के संभावित रिटर्न का अनुमान काफी हद तक लगाया जा सकता है।  

रिटर्न का अनुमान आत्मविश्वास के साथ लगाने के लिए आपको अपने एक्सपेक्टेड वार्षिक रिटर्न में से पोर्टफोलियो वैरियंस को घटाना और जोड़ना पड़ेगा। ऐसा करने से आपको पता चल जाएगा कि एक साल में आपका पोर्टफोलियो कितना गंवा सकता है या कितना कमा सकता है।

तो यह कहा जा सकता है कि नॉर्मल डिस्ट्रीब्यूशन के आधार पर हम काफी हद तक यह बता सकते हैं कि हमारा पोर्टफोलियो किस रेंज में ऊपर या नीचे हो सकता है। यह अनुमान भरोसे के तीन अलग-अलग स्तरों पर लगाया जा सकता है –

• स्तर 1 – एक स्टैन्डर्ड डेविएशन की दूरी पर, 68% भरोसे के साथ
• स्तर 2 – दो स्टैन्डर्ड डेविएशन की दूरी पर, 95% भरोसे के साथ
• स्तर 3 – तीन स्टैन्डर्ड डेविएशन की दूरी पर, 99% भरोसे के साथ

याद रखिए कि वैरियेंस को स्टैंडर्ड डेविएशन में नापा जाता है। यहां पर यह ध्यान देना जरूरी है कि पोर्टफोलियो का वार्षिक वैरियंस जो कि 17.64% है, वह 1 स्टैंडर्ड डेविएशन है। 

तो अगर 17.64% 1 स्टैंडर्ड डेविएशन है तो 2 स्टैंडर्ड डेविएशन होगा 17.64% * 2 = 35.28% और 3 स्टैंडर्ड डेविएशन होगा 17.64% * 3 = 52.92% । 

अगर आप यह सब पहली बार पढ़ रहे हैं तो मुझे पक्का पता है कि आपको ये समझ में नहीं आ रहा होगा। इसीलिए यह जरूरी है कि आप नॉर्मल डिस्ट्रीब्यूशन के बारे में पढ़ें और जानें। इसे मैंने ऑप्शन के अध्याय में बताया था।

7.2 – पोर्टफोलियो के रेंज अनुमान लगाना

अब हमारे पास वार्षिक वैरियंस (17.64%) और एक्सपेक्टेड एनुअल रिटर्न यानी वार्षिक रिटर्न (55.4%) है। इसके आधार पर अब हम यह अनुमान लगा सकते हैं कि पोर्टफोलियो का रिटर्न अगले साल किस रेंज या दायरे में रह सकता है। ध्यान दें कि जब हम एक दायरे या रेंज की बात कर रहे हैं तो यह हम यह बताने की कोशिश कर रहे हैं कि इसके ऊपर और नीचे जाने की सीमा क्या होगी। 

ऊपर की सीमा की संख्या निकालने के लिए हमें अपने वार्षिक पोर्टफोलियो वैरियेंस में एक्सपेक्टेड एनुअल रिटर्न को जोड़ना है, यानी 17.64% + 55.4% = 72.79% , दायरे की निचली सीमा निकालने के लिए हमें वार्षिक पोर्टफोलियो वैरियेंस में से एक्सपेक्टेड वार्षिक रिटर्न को घटाना है, यानी 55.4%  – 17.64% = 37.51%  

तो अगर आप मुझसे पूछे कि अगले 1 साल में मेरे 5 स्टॉक के पोर्टफोलियो में रिटर्न कैसा रह सकता है, तो मेरा जवाब होगा कि रिटर्न 37.51% से लेकर 72.79% तक के बीच में होगा। 

अब यहां पर 3 सवाल खड़े हो सकते हैं 

1. रिटर्न का यह रेंज हमें बता रहा है कि पोर्टफोलियो में पैसा डूबने की कोई संभावना नहीं है, यह कैसे संभव है? यह तो बता रहा है कि बुरी से बुरी हालत में भी 37.51% का रिटर्न मिलेगा जो कि बहुत ही ज्यादा अच्छा है। 

• मैं मानता हूं कि यह बात सही है लेकिन सच्चाई भी यही है कि रेंज यानी दायरे की गणना सांख्यिकी के आधार पर की गई है। ध्यान रहे कि अप्रैल से मई 2017 के इस दौर में (जब मैं इसको लिख रहा हूं) बाजार में बुल रन चल रहा था और हमने जो स्टॉक चुने हैं उन्होंने इस दौरान बहुत ही ज्यादा अच्छा प्रदर्शन किया था, इसीलिए यह सारे आंकड़े बहुत ही ज्यादा पॉजिटिव दिखाई दे रहे हैं। अगर हमने 1 साल से ज्यादा के आंकड़े लिए होते तो यह रेंज एकदम ही अलग तस्वीर पेश कर रहा होता। लेकिन यहां पर हमारे लिए यह बात महत्वपूर्ण नहीं है। महत्वपूर्ण बात यह है कि हमें यह सीखना है कि रेंज या दायरा कैसे निकाला जाता है

1. तो आपको यह तो समझ आ गया कि रेंज को निकालने में कोई गलती नहीं हुई है, लेकिन इस बात की क्या गारंटी है कि पोर्टफोलियो रिटर्न 37.15% से लेकर 72.79% के बीच में ही रहेगा?

• जैसा कि मैं पहले भी कह चुका हूं कि हम स्तर एक पर हैं यानी 1 स्टैंडर्ड डेविएशन पर, इसलिए इस बात की संभावना 68% है। 

1. अगर मुझे इससे ज्यादा भरोसा चाहिए तो 

• ऐसी स्थिति में आपको हुए बड़े स्टैंडर्ड डेविएशन के साथ इसको निकालना पड़ेगा 

आइए अब यही करते हैं, 

इस रेंज को 95% भरोसे के साथ निकालने के लिए हमें दूसरे स्टैंडर्ड देविएशन पर जाना होगा, मतलब हमें पहले स्टैंडर्ड डेविएशन से मिली हुई संख्या को 2 से गुणा करना होगा। हम पहले भी यह कर चुके हैं इसलिए हमें पता है कि दूसरा स्टैंडर्ड देविएशन 35.28% का होता है। 

इसके आधार पर हम 95% भरोसे के साथ अगले 1 साल के लिए इस पोर्टफोलियो का रिटर्न होगा 

दायरे की निचली सीमा =  55.15% – 35.28% = 19.87%

दायरे की ऊपरी सीमा =  55.15% +  35.28% = 90.43%

हम अपने कॉन्फिडेंस यानी भरोसे को और भी बढ़ा कर 99% तक ले जा सकते हैं। इसके लिए हमें बस अपने रिटर्न के रेंज को तीसरे स्टैंडर्ड डेविएशन तक ले जाना होगा आपको याद है कि तीसरा स्टैंडर्ड डेविएशन 52.92% होता है – 

दायरे की निचली सीमा =  55.15% – 52.92% = 2.23%

दायरे की ऊपरी सीमा =  55.15% +  52.92% = 108.07%

जैसा कि आपको दिख रहा होगा कि हम जैसे जैसे अपने भरोसे का स्तर बढ़ाते जाते हैं, वैसे वैसे हमारा रेंज या दायरा भी बढ़ता जाता है। इस अध्याय के अंत में मैं आपके लिए कुछ अभ्यास छोड़ जा रहा हूं 

1. इन पांच स्टॉक के पोर्टफोलियो के फ्रिकवेंसी डिस्ट्रीब्यूशन (Frequency Distribution) को प्लॉट कीजिए और इसके डिस्ट्रीब्यूशन को देखकर यह बताइए कि क्या आपको यहां पर कोई बेल कर्व दिख रहा है?
2. हमने यहां पर 1 साल के लिए दायरा या रेंज निकाला है लेकिन अगर आपको 3 महीने के लिए रेंज को निकालना हो या 3 हफ्ते के लिए रेंज को निकालना हो तो आप क्या करेंगे?

आप इसका जवाब नीचे कमेंट सेक्शन में लिख सकते हैं। आप इस एक्सेल शीट को यहां से डाउनलोड– download कर सकते हैं।

इस अध्याय की मुख्य बातें 

1. पोर्टफोलियो का रिटर्न इस बात पर निर्भर करता है कि अलग-अलग स्टॉक का पोर्टफोलियो में कितना वजन है 
2. किसी स्टॉक का पोर्टफोलियो के रिटर्न पर कितना असर पड़ेगा यह जानने के लिए उस स्टॉक के औसत रिटर्न को उसके स्टॉक के वजन से गुणा करना होता है 
3. किसी पोर्टफोलियो का कुल एक्सपेक्टेड रिटर्न उस में शामिल अलग-अलग स्टॉक के एक्सपेक्टेड रिटर्न का जोड़ होता है 
4. हर दिन के वैरियंस यानी डेली वैरियेंस को वार्षिक वैरियंस में बदला जा सकता है इसके लिए बस उसे 252 के वर्गमूल/स्कैवयर रूट से गुणा करना होता है 
5. जब भी हम किसी पोर्टफोलियो का वैरियंस निकालते हैं तो वह पहले स्टैंडर्ड डेविएशन पर होता है 
6. दूसरे और तीसरे स्टैंडर्ड डेविएशन का वैरियंस निकालने के लिए उसे 2 या 3 से गुणा करना पड़ता है 
7. किसी पोर्टफोलियो का एक्सपेक्टेड रिटर्न एक दायरे के तौर पर निकाला जाता है
8. इस रेंज को पाने के लिए हमें पोर्टफोलियो के एक्सपेक्टेड रिटर्न में से वैरियंस को घटाना या जोड़ना होता है।
9. हर स्टैन्डर्ड डेविएशन के साथ भरोसे का एक स्तर जुड़ा होता है, भरोसे के स्तर को बढ़ाने के लिए ऊंचे स्टैन्डर्ड डेविएशन का इस्तेमाल करना होता है