Say Hello to The Greeks!

To learn more about options, check out this module on Varsity.

Why are the Option Greeks important?

What do you think makes a bollywood movie successful at the box office? Chances are you’d say – the success of the movie depends on the lead actors. Well, this is true to some extent. But in reality the success heavily depends on few other variables such as – the story line, the director, the songs, the dance, cinematography, and the works.

Drawing parallels, what according to you is required for a successful options trade? Chances are you’d say the success depends on which direction the market moves. Well, this is true to some extent, however this is equivalent to saying the movie’s success depends on just the lead actors. In reality, besides the direction of the market, the success of an option trade depends on..

• The rate at which the markets move
• The volatility aka the swings in the market
• Passage of time

These variables which influence the option trade are called ‘The Option Greeks’.

Delta – The Direction Matters

The delta, a constantly varying number, is a measure of how an option’s value changes with respect to change in the price of the underlying contract. In simpler terms, delta helps you answer the question “By how much will the option’s premium change for every 1 point change in the underlying price”. For example, assume you buy 7,800 Call option when Nifty is at 7,775. After you buy the option, assume the market moves by 25 points, and hits 7,800. For the 25 point move in the market, by how many points will the option premium increase from Rs.48? The answer to this lies with the delta.

The Delta from a call option perspective

The call option delta is a number which ranges between 0 and 1. For instance, an option has a delta of 0.4, then for every 1 point change in the underlying price, we can expect the premium to vary by 0.4 point. In the initial example, assuming 7,800 call option has a delta of 0.5, for a 25 point move in Nifty (underlying), the premium is likely to change by 12.5 points (0.5 x 25), hence the premium is expected to goto 60.5 (48 +12.5) from 48.  

The Delta from a put option perspective

Put options have characteristics similar to call options, except that they move in the opposite direction of the underlying market. When the underlying gains, put premium goes down and vice versa. Hence put options’ delta ranges for -1 to 0. Meaning if the put option has a delta of  -0.5, then for every 1 point up/down move in the market the put premium loses/gain 0.5 points. For example, assume the 7,700 Nifty put option is trading at 30 when the underlying i.e Nifty spot is trading at 7800. Also assume the delta for this option as -0.3. If the market were to move to 7830 from 7800, the premium is likely to change by – 9 (-0.3 x 30) points. Hence the new premium will be -9 + 30 = 21.

The Delta quick reckoner

You can use the following table to approximately guess the delta of an option. Needless to say, the exact values can be determined by using an options calculator, however use this table to intelligently estimate the delta on the following. Assume you buy TCS 2,600 put option when the underlying trading at 2,550. You immediately recognize that the 2600 put option is ‘In the money’; hence as per the above table, the delta should be between -1 and -0.5. So, for any option, identify its moneyness (ITM, OTM or ATM) ,and match it with the values as indicated in the above table.

Also, think about the delta as a probability of the option to expire in the money. For example, if a call option has a delta of 0.4, then clearly from the table above we know that the option must be an OTM call option. The probability of this particular OTM call option to expire as ITM option by expiry is 40% (0.4*100). Similarly if the delta is 0.7, it means there is a 70% chance that this option will expire as ITM by expiry.

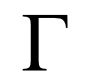 The Gamma – Rate of change of delta

Gamma is a slightly complicated greek. It is best understood with an example. Think about this situation – TCS is  at 2,550, the strike under consideration is 2,650 Call option. Clearly the option is OTM. So the delta must be  somewhere between 0 and 0.5. Let us assume the delta is 0.3. Assume, the stock moves, and TCS is now at 2,650. This also means the option has transitioned from OTM to ATM…which also means the delta has moved to 0.5 from 0.3. The illustration above clearly indicates one thing i.e the delta is a changing variable. The Gamma also referred to as the curvature of the option, gives us the rate at which the option’s delta changes as the underlying changes. The gamma is usually expressed in deltas gained or lost per one point change in the underlying. Unlike the delta, the gamma is always a positive number for both calls, and puts.

Let us consider a Nifty example again. Assume Nifty is at 7,800, its delta is 0.5, and the gamma is 0.003. If Nifty moves by 30 points taking the spot to 7,830, the delta obviously changes. It changes by extent of 0.003 points for every 1 point move in underlying. So for a 30 point move, the 0.09 deltas are added upward. The calculation is as follows of the new delta is as follows..

New Delta = Old delta + (Gamma x Movement in the underlying)

= 0.5 + (0.003 x 30)

=0.5+ 0.09

= 0.59

Needless to say, the gamma itself changes; in mathematical parlance the rate of change of gamma is captured by Vomma, a 2^nd order derivative of Gamma. For all practical purposes, this is not really important for a retail trader. But do remember ‘the vomma’ if you want to flaunt your greek skills in the next cocktail party 🙂

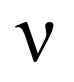The Vega – Impact of volatility

The Vega of an option measures the rate of change of option’s premium with every percentage change in volatility. The vega helps us answer this question..”What is the likely change in the option premium because of a % change in volatility?” All options, irrespective of calls or puts gain value if the volatility increases. As volatility increase, the likelihood of the option expiring ITM increases. Therefore since options gain value with increase in volatility, the vega is a positive number, for both calls and puts.

For example – If the premium of an option is 3.25 at 20% volatility, and the vega is 0.15. The premium increases to 3.40 when the volatility increases to 21%. Likewise the premium drops to 3.10 when the volatility decreases to 19%.

All else equal, the ATM option will always tend to have a higher Vega compared to OTM and ITM options. This means to say that the ATM option is the most sensitive in total points to a change in volatility. As a corollary, the OTM option is always the most sensitive in percentage terms to a change in volatility.

To illustrate – A call option at 15% volatility assumption, suppose ATM and OTM option is trading @ 2.00 and 0.50 respectively. If we raise the volatility to 20% the option might now trade @ 3.00 and 1.00 respectively. Notice, the ATM option has shown a greater point increase (1 vs 0.5) but percentage wise, OTM has shown a greater increase (50% vs 100%).

You may have heard of stories about traders doubling their capital trading OTM options, well this is one of the reasons why they double!

The Theta – The importance of time

Options – Both calls and puts lose value as expiration approaches. The Theta or time decay factor is the rate at which an option loses value as time passes. In simpler words, it helps us answer this question – “How many points the option premium will erode for each day that passes by”. Therefore, the Theta is expressed in points lost per day when all other conditions remain the same.

Time runs in one direction, hence theta is always a positive number, however to remind traders as it’s a loss in options value it is sometimes written as a negative number.  For example, If an option is trading at 2.75 with theta of -0.5, all else equal the option should trade at 2.70 the following day.

As we get closer to expiration, the rate at which option losses money accelerates, and therefore the premium. The erosion of premium is called ‘The Time Decay’. Due to the effect of time decay, options are considered to be a depreciating asset. Here is a graph that shows how the option premium varies as time to expiry approaches closer.

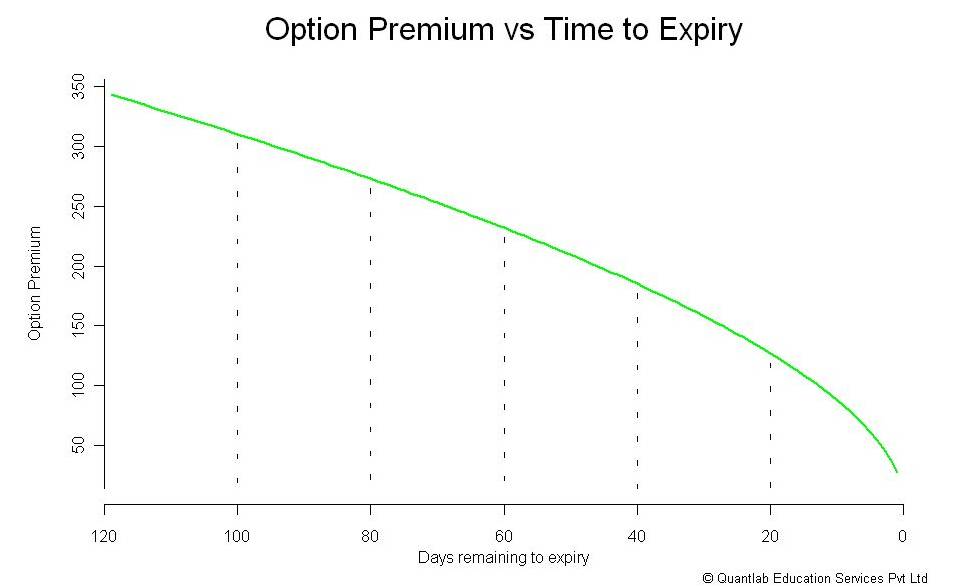Notice how the drop accelerates in the last bit. This is why, it makes a lot of sense to write options as and when we approach expiry. For a long option theta will be negative – meaning every day that passes by, there is a minor loss in premium, which translates as a loss to the option buyer, hence the negative sign.

Similarly when you write options, loss of premium because of the passage of time is good news. Hence the theta is associated with a positive sign for short options.

A note on Vega and Theta

The Vega of all option declines as expiration approaches. This also highlights an important principle while evaluating options…both time and volatility are closely interconnected!

• More time to expiry implies more time for volatility to take effect, likewise lesser the time to expiry, lesser the time for volatility to affect the premiums
• When there is less time to expiry, even if volatility increases, it will have only a minor effect on an option value

So the next time if you ever wonder why the premiums are not increasing in spite of an increased volatility, make sure you check the time to expiry!

Taking this forward

Now that you know what the ‘Option Greeks’ are all about, we need to figure out how to practically use these Greeks for making better trading decision.

Identifying the best option strikes to trade considering the time to expiry is the key to successful option trading. Option Greeks helps the trader with just this. We will discuss the practical application of ‘The Option Greek’ in the next post.

Stay tuned!