4.1- टाइम इज मनी – Time is Money – समय ही धन है
आपको वो पुरानी कहावत याद होगी टाइम इज मनी यानी समय ही धन है। ऐसा लगता है यह कहावत ऑप्शन ट्रेडिंग के लिए बिल्कुल सही है। कुछ देर के लिए ग्रीक्स के बारे में बातचीत को बिल्कुल भूल जाइए और एक बहुत ही जरूरी आधारभूत सिद्धांत पर वापस लौटते हैं जो कि समय से जुड़ा है। मान लीजिए आपने किसी प्रतियोगिता में हिस्सा लिया है। आप बहुत तेज हैं और आपके पास वह क्षमता है कि आप उस प्रतियोगिता को जीत सकते हैं। लेकिन अगर आपके पास समय ना हो और आप अपनी तैयारी ठीक से ना कर पाए तो आप यह परीक्षा पास नहीं कर पाएंगे। ऐसे में इस परीक्षा में सफल होने की संभावना कितनी है? यह इस पर निर्भर करता है कि आप परीक्षा की तैयारी के लिए कितना समय निकालते हैं और कितनी तैयारी करते हैं? इस बात को ध्यान में रखते हुए आगे बढ़ते हैं
| तैयारी के लिए दिनों की संख्या | उतीर्ण होने की संभावना |
|---|---|
| 30 दिन | Very high बहुत अधिक |
| 20 दिन | High अधिक |
| 15 दिन | Moderate सीमित |
| 10 दिन | Low कम |
| 5 दिन | Very low बहुत कम |
| 1 दिन | Ultra low सबसे कम |
साफ है कि जितने ज्यादा दिनों की तैयारी होगी सफल होने की संभावना भी उतनी ही ज्यादा होगी। अब इसी बात को ध्यान में रखते हुए एक नई स्थिति पर विचार करते हैं- निफ्टी का स्पॉट 8500 पर है, आप निफ्टी 8700 कॉल ऑप्शन लेते हैं- इस बात की संभावना कितनी है कि आपका कॉल ऑप्शन एक्सपायरी पर इन द मनी(ITM) बन सके। इसी सवाल को मैं एक दूसरे तरीके से पूछता हूं-
-
- अगर निफ्टी आज 8500 पर है तो इस बात की कितनी संभावना है कि अगले 30 दिनों में निफ्टी 200 प्वाइंट ऊपर चला जाए, और 8700 CE का ऑप्शन ITM बन सके?
- निफ्टी के अगले 30 दिनों में 200 प्वाइंट पर चढ़ने की संभावना काफी अधिक है इसलिए यह ऑप्शन ITMबन सके इसकी संभावना काफी ज्यादा है
- लेकिन अगर एक्सपायरी में सिर्फ 15 दिन हो?
- तो अगले 15 दिनों में भी निफ्टी के ऊपर जाने की कुछ न कुछ संभावना जरूर है इसलिए इस बात की संभावना भी है कि यह ऑप्शन ITM ऑप्शन बन सके आप इसकी संभावना ज्यादा मान सकते हैं
-
- अब मान लीजिए कि एक्सपायरी में सिर्फ 5 दिन बचे हैं, तो?
- अगले 5 दिनों में निफ्टी का 200 प्वाइंट बढ़ने की संभावना काफी कम है इसलिए 8700 CE ऑप्शन के ITM बनने की संभावना भी कम है।
-
- लेकिन अगर एक्सपायरी में सिर्फ 1 दिन बचा हो तो ?
- 1 दिन में निफ्टी के 200 प्वाइंट बढ़ने की संभावना बहुत ही कम है इसलिए मैं मान सकता हूं कि आप्शन के इन द मनी(ITM ) बनने की संभावना काफी कम है
ऊपर की बातचीत से हम क्या निष्कर्ष निकाल सकते हैं? साफ है कि एक्सपायरी के लिए जितना ज्यादा समय बचा होगा ऑप्शन के इन द मनी (ITM) एक्सपायर होने की संभावना भी उतनी ही ज्यादा होगी। इस बात को ध्यान में रखिए। अब हम अपना फोकस ऑप्शन बेचने वाले पर करते हैं। हमें पता है कि ऑप्शन बेचने वाला ऑप्शन बेचकर प्रीमियम प्राप्त करता है। हमें यह भी पता है कि उसका रिस्क असीमित है और उसको मिलने वाला मुनाफा सीमित है। उसे मुनाफा उतना ही होगा जितना उसे प्रीमियम मिलेगा । वह इस प्रीमियम को अपने पास पूरी तरीके से तभी रख पाएगा जब ऑप्शन जीरो पर एक्सपायर हो। अब जरा सोचिए अगर वह महीने की शुरुआत में एक ऑप्शन बेचता है तो अच्छी तरह से जानता है कि-
- उसको मिलने वाला मुनाफा सीमित है जबकि उसका रिस्क असीमित है
- वह यह भी जानता है कि समय की वजह से इस बात की संभावना है कि जो भी ऑप्शन वह बेच रहा है वह इन द मनी बन सके इसका मतलब है कि उसको अपने प्रीमियम बचाने का या मुनाफा बचाने की संभावना कम है
वास्तव में किसी भी समय किसी भी ऑप्शन की एक्सपायरी पर इन द मनी बनने की संभावना काफी ज्यादा है अगर एक्सपायरी में। समय हो लेकिन जैसे-जैसे एक्सपायरी पास आती जाती है वैसे वैसे यह संभावना कम से कम होती जाती है। यह जानने के बाद क्या कोई ऑप्शन बेचने वाला ऑप्शन बेचना चाहेगा? जब आपको पता है कि जो ऑप्शन को आप बेच रहे हैं उस ऑप्शन के इन द मनी होकर एक्सपायर होने की संभावना काफी ज्यादा है क्योंकि समय काफी है। इसका मतलब है कि ऑप्शन बेचने वाले के लिए “समय” एक रिस्क की तरह काम करता है। लेकिन अगर ऑप्शन खरीदने वाला ऑप्शन बेचने वाले को एक ऐसा लालच दे जो कि समय से होने वाले उसके रिस्क को कम कर सके तो क्या होगा? ऐसे में यह सोचना पड़ेगा कि रिस्क ज्यादा है या उसके मुकाबले मिलने वाला मुनाफा? वास्तव में ऑप्शन के बाजार में यही होता है, जब आप ऑप्शन के लिए प्रीमियम दे रहे होते हैं तो वास्तव में आप इन चीजों के लिए पैसे दे रहे होते हैं
- समय से जुड़ा रिस्क
- ऑप्शन की अंतर्निहित या इंट्रिसिक वैल्यू
दूसरे शब्दों में कहें तो प्रीमियम = टाइम वैल्यू + इंट्रिन्सिक वैल्यू
आपको याद होगा कि कि मॉड्यूल के शुरू में हमने यह बताया था कि इंट्रिन्सिक वैल्यू वह राशि होती है जो आपको तब मिलती हैं जब आप अपने ऑप्शन को आज ही एक्सरसाइज कर लें। आपकी याद को ताजा करने के लिए एक बार हम कुछ ऑप्शन की इंट्रिन्सिक वैल्यू निकालते हैं, यह मानते हुए कि निफ्टी 8423 पर है-
- 8350 CE
- 8450 CE
- 8400 PE
- 8450 PE
हमें पता है कि किसी भी ऑप्शन की इंट्रिन्सिक वैल्यू हमेशा पॉजिटिव होती है या जीरो होती है जीरो के नीचे कभी नहीं जाती अगर किसी वजह से इंट्रिसिक वैल्यू नेगेटिव में दिखती है तो भी उस इंट्रिसिक वैल्यू को जीरो मान लिया जाता है। हमें पता है कि कॉल ऑप्शन की इंट्रिसिक वैल्यू स्पॉट कीमत – स्ट्राइक कीमत और पुट ऑप्शन के लिए स्ट्राइक कीमत – स्पॉट कीमत इसलिए ऊपर दिए गए ऑप्शन की इंट्रिन्सिक वैल्यू होगी –
- 8350 CE = 8423 – 8350 = 73
- 8450 CE = 8423 – 8450 = -ve संख्य़ा इसलिए 0
- 8400 PE = 8400 – 8423 = -ve संख्य़ा इसलिए 0
- 8450 PE = 8450 – 8423 = 27
हम जानते हैं कि इंट्रिन्सिक वैल्यू कैसे निकाली जाती है इसलिए कोशिश करते हैं कि हम प्रीमियम को इंट्रिन्सिक वैल्यू और टाइम वैल्यू के दो हिस्सों में बांट कर देख सकें। एक नजर इस स्नैपशॉट पर डालिए-
जिन चीजों पर आपको ध्यान देना है वह हैं
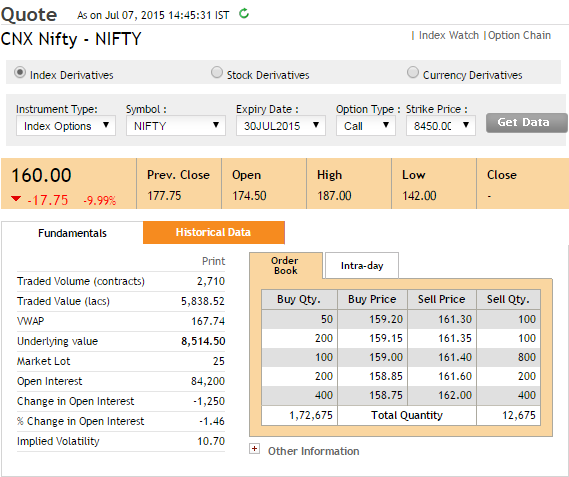
- स्पॉट कीमत = 8531
- स्ट्राइक = 8600 CE
- स्टेटस = OTM
- प्रीमियम = 99.4
- तारीख = 6 जुलाई 2015
- एक्सपायरी = 30 जुलाई 2015
कॉल ऑप्शन की इंट्रिन्सिक वैल्यू – स्पाट कीमत – स्ट्राइक कीमत यानी 8531 – 8600 = 0 (निगेटिव संख्या होने की वजह से) हमें पता है कि प्रीमियम = टाइम वैल्यू + इंट्रिन्सिक वैल्यू तो प्रीमियम ( 99.54) = टाइम वैल्यू + 0 =99.54 तो आप देख सकते हैं कि बाजार प्रीमियम में 99.4 रुपए देने को तैयार है ऐसे ऑप्शन के लिए जिसकी इंट्रिन्सिक वैल्यू जीरो है जबकि टाइम वैल्यू काफी ज्यादा है। अब आपको समझ में आ गया होगा कि ऑप्शन में टाइम इज मनी। अब इसी स्नैपशॉट को को फिर से देखिए जब मैंने इसको अगले दिन यानी 7 जुलाई को लिया।
आपको दिखेगा की अंडरलाइंग की कीमत थोड़ी ज्यादा बढ़ गई है (8538)। लेकिन इसके बावजूद ऑप्शन का प्रीमियम कम हो गया है। इसको हम फिर से इंट्रिसिक वैल्यू और टाइम वैल्यू में बांट कर देखते हैं। स्पॉट कीमत – स्ट्राइक कीमत i.e. 8538 – 8600 =0 (निगेटिव संख्या होने की वजह से)। हमें पता है कि प्रीमियम 87.9 = टाइम वैल्यू + इंट्रिन्सिक वैल्यू। टाइम वैल्यू + 0 = 87.9 । इसका मतलब है कि टाइम वैल्यू = 87.9 । तो एक रात में प्रीमियम घट गया। ऐसा क्यों हुआ, इसको हम थोड़ी देर में समझेंगे। इस उदाहरण में प्रीमियम 99.4 – 87.9 = 11.5 कम हो गया। यह गिरावट दो वजह से है वोलैटिलिटी और समय । वोलैटिलिटी के बारे में हम अगले अध्याय में बात करेंगे। इस बात को ठीक से समझने के लिए अगर हम मान लें कि वोलैटिलिटी और स्पॉट स्थिर हैं तो प्रीमियम में गिरावट पूरी तरीके से समय की कम होने की वजह से होगी। अगर ऐसा होता तो मुझे लगता है कि यह गिरावट ₹5 से ज्यादा नहीं होती। यह 11.5 तो बिल्कुल भी नहीं होगी। एक और उदाहरण देखते हैं
- स्पॉट कीमत = 8514.5
- स्ट्राइक = 8450 CE
- स्टेटस = ITM
- प्रीमियम = 160
- तारीख = 7 जुलाई 2015
- एक्सपायरी = 30 जुलाई 2015
कॉल ऑप्शन की इंट्रिन्सिक वैल्यू = स्पॉट कीमत – स्ट्राइक कीमत i.e. 8514.5 – 8450 = 64.5 । हमें पता है प्रीमियम = टाइम वैल्यू + इंट्रिन्सिक वैल्यू 160 = टाइम वैल्यू + 64.5. इसका मतलब है कि टाइम वैल्यू = 160 – 64.5 = 95.5 । मतलब ₹160 के कुल प्रीमियम में से ट्रेडर ₹64.50 इंट्रिन्सिक वैल्यू के लिए दे रहे हैं और ₹95.5 समय या टाइम वैल्यू के लिए दे रहे हैं। आप किसी भी ऑप्शंन के लिए( कॉल और पुट दोनों ) यह गणना कर सकते हैं और प्रीमियम को टाइम वैल्यू और इंट्रिन्सिक वैल्यू में बांट कर देख सकते हैं।
14.2 समय की चाल
जैसा कि हमें पता ही है कि समय एक ही दिशा में चलता है। अगर एक्सपायरी की तारीख को एक टारगेट टाइम या लक्ष्य मानें तो समय की चाल किस दिशा में होगी। जैसे जैसे समय चलेगा वैसे वैसे एक्सपायरी के दिनों की संख्या कम होती जाएगी। ऐसे में एक मैं आपसे एक सवाल पूछता हूं – एक्सपायरी 18 दिन बचे हैं तो ट्रेडर समय की कीमत के तौर पर ₹100 तक देने को तैयार हैं, लेकिन अगर एक्सपायरी में 5 दिन बाकी हों तो क्या वह यही रकम देने को तैयार होंगे? शायद नहीं, एक्सपायरी में कम समय बचे होने की वजह से ट्रेडर टाइम वैल्यू के लिए कम पैसे देंगे। इसके कुछ महीनों पहले मैंने एक स्नैपशॉट लिया था उसको देखिए
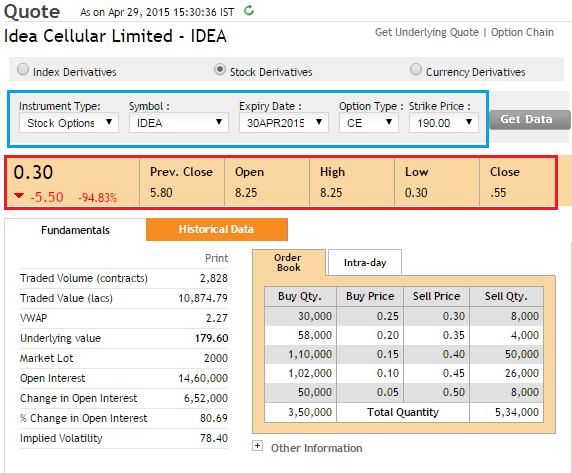
- तारीख = 29 अप्रैल
- एक्सपायरी = 30 अप्रैल
- एक्सपायरी में समय = एक दिन
- स्ट्राइक = 190
- स्पॉट = 179.6
- प्रीमियम = 30 पैसा
- इंट्रिसिक वैल्यू = 179.6 – 190 = 0 (क्योंकि यह नेगेटिव है )
इसलिए टाइम वैल्यू सिर्फ 30 पैसा है जोकि प्रीमियम है
तो एक्सपायरी में 1 दिन बच् होने पर ट्रेडर 30 पैसे ही प्रीमियम के तौर पर दे रहे हैं जो कि टाइम वैल्यू है। लेकिन अगर एक्सपायरी में 20 दिन बचे होते या ज्यादा दिन बचे होते तो शायद यह वैल्यू ₹5 या ₹8 भी हो सकती थी। मैं यह समझाने की कोशिश कर रहा हूं कि हर एक दिन गुजरने के साथ-साथ जैसे-जैसे हम एक्सपायरी के करीब पहुंचते हैं, एक्सपायरी के लिए समय कम होता जाता है और इसका मतलब है कि ऑप्शन को खरीदने वाला कम से कम पैसे टाइम वैल्यू फ्री देना चाहता है। इसलिए ऑप्शन खरीदने वाला अगर आज ₹10 टाइम वैल्यू के तौर पर देने को तैयार है तो कल शायद वह ₹9.5 ही देने को तैयार होगा। इससे एक बहुत ही महत्वपूर्ण निष्कर्ष निकलता है- अगर बाकी सभी चीजें स्थिर रहे तो एक ऑप्शन एक डिप्रेसिएटिंग एसेट है यानी इसकी वैल्यू समय के साथ कम होती जाती है। ऑप्शन का प्रीमियम हर दिन गिरता है और इसको समय कम होते जाने के के परिणाम के तौर पर देखा जा सकता है ।तो अब अगला सवाल यह है कि है हर दिन प्रीमियम कितना घटेगा? तीसरा ऑप्शन ग्रीक यानी थीटा इसी सवाल का जवाब देता है।
14.3 थीटा – Theta
जैसे जैसे एक्सपायरी करीब आती है सभी ऑप्शन( कॉल और पुट दोनों )की वैल्यू यानी मूल्य कम होता जाता है। थीटा या टाइम डीकेय (Time Decay) फैक्टर समय के साथ ऑप्शन की कीमत कम होने की दर को बताता है। थीटा को प्वाइंट गिरावट प्रतिदिन के तौर पर बताया जाता है जबकि बाकी सभी स्थितियां स्थिर हों। समय सिर्फ एक ही दिशा में चलता है इसलिए थीटा हमेशा एक पॉजिटिव नंबर होता है। लेकिन ये याद दिलाने के लिए कि इसमें ऑप्शन की कीमत कम हो रही है कई बार इसे निगेटिव नंबर के तौर पर लिखा जाता है। अगर थीटा -0.5 है तो ये यह बताता है कि ऑप्शन का प्रीमियम हर दिन -0.5 की दर से कम हो रहा है। उदाहरण के तौर पर (अगर कोई ऑप्शन ₹2.75 पर ट्रेड हो रहा है और उसका थीटा – 0.05 है तो अब अगले दिन यह ₹2.70 पर ट्रेड होगा, अगर बाकी सभी चीजें स्थिर हो तो)। एक लॉन्ग ऑप्शन यानी ऑप्शन का खरीदार के लिए थीटा हमेशा निगेटिव होगा इसका मतलब है कि ऑप्शन के खरीदार के लिए नुकसान हर दिन बढ़ता जाएगा। ऑप्शन बेचने वाले या शार्ट ऑप्शन के लिए अब थीटा हमेशा पॉजिटिव होगा, थीटा ऑप्शन बेचने वाले के लिए एक दोस्त ग्रीक है। आपको याद होगा कि ऑप्शन बेचने वाले के लिए प्रीमियम को बचाए रखना ही सबसे महत्वपूर्ण होता है इसलिए अगर हर दिन ऑप्शन की वैल्यू कम हो रही है तो ऑप्शन बेचने वाले का मुनाफा बचे रहने की संभावना लगातार बढ़ रही है। उदाहरण के तौर पर एक अगर ऑप्शन बेचने वाले ने ₹54 पर ऑप्शन बेचा है और उसका थीटा 0.75 है तो अगर बाकी सभी चीज स्थिर है तो ये ऑप्शन तीन दिन बाद 0.75*3 = 2.25 =54 -2.25 = 51.75 पर ट्रेड होगा। ऐसे में ऑप्शन बेचने वाला अपने ऑप्शन पोजीशन T+3 डे पर बंद कर सकता है और इसे ₹51.75 पर खरीद कर ₹2.25 पैसे का मुनाफा कमा सकता है। यह मुनाफा उसे थीटा की वजह से होगा। इस ग्राफ पर नजर डालिए-
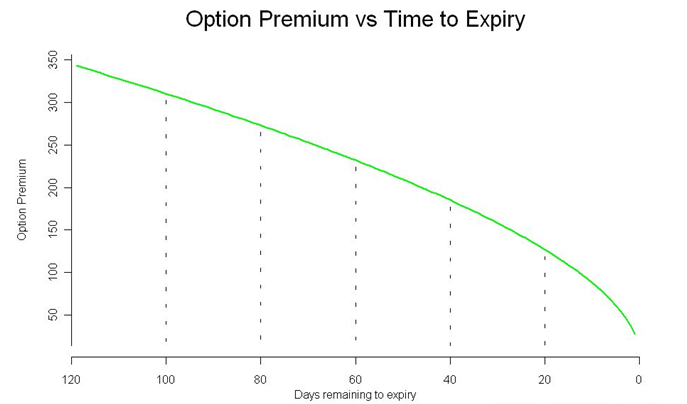
यह ग्राफ हमें बताता है कि कैसे एक्सपायरी का समय करीब आने के साथ साथ प्रीमियम कम होता जाता है। इसे टाइम डीकेय (Time Decay) ग्राफ भी कहते हैं। हम इसमें इन चीजों को देख सकते हैं-
- सीरीज के शुरू होने के समय- जब एक्सपायरी में काफी दिन बचे हुए हैं तो ऑप्शन का मूल्य ज्यादा तेजी से कम नहीं होता। उदाहरण के तौर पर जब एक्सपायरी में 120 दिन बचे हैं तो ऑप्शन 350 पर ट्रेड हो रहा है लेकिन जब एक्सपायरी को केवल 100 दिन बचे हैं तो भी ऑप्शन 300 पर ट्रेड हो रहा है। इसका मतलब है कि थीटा का असर कम है।
- जब हम एक सीरीज के एक्सपायरी के पास पहुंचते हैं- थीटा का असर काफी ज्यादा है। ध्यान दीजिए कि जब एक्सपायरी को सिर्फ 20 दिन बचे हैं तो ऑप्शन 150 पर ट्रेड हो रहा था लेकिन जब हम एक्सपायरी की तरफ बढ़ते हैं तो प्रीमियम में गिरावट आती है और यह गिरावट तेजी से बढ़ती है (ऑप्शन 50 के नीचे पहुंच जाता है)
तो अगर आप सीरीज के शुरुआत में ऑप्शन बेच रहे हैं तो आपको एक ज्यादा बड़ा प्रीमियम मिल सकता है (क्योंकि टाइम वैल्यू काफी ज्यादा है)। लेकिन याद रखिए कि प्रीमियम में में गिरावट की गति कम होती है। आप ऑप्शन को एक्सपायरी के करीब बेचेंगे तो आपको प्रीमियम कम मिलेगा लेकिन प्रीमियम में गिरावट तेजी से बढ़ेगी जो कि ऑप्शन बेचने वाले के लिए फायदे का सौदा होगा। थीटा एक बड़ा ही सीधा साधा और आसान सा ग्रीक है। इसको समझना आसान है। हम जब ग्रीक्स के आपसी संबंधों की बात करेंगे तब एक बार हम फिर से थीटा पर नजर डालेंगे।
लेकिन अगर अभी के लिए अब जाने का समय है। अगले अध्याय में हम अंतिम ग्रीक वेगा को समझेंगे।
इस अध्याय की मुख्य बातें
- ऑप्शन बेचने वाले को हमेशा टाइम रिस्क के लिए पैसे मिलते हैं।
- प्रीमियम = इंट्रिन्सिक वैल्यू + टाइम वैल्यू
- अगर बाकी सारी चीजें एक बराबर या स्थिर हों तो भी ऑप्शन हर दिन थीटा की वजह से पैसे गंवाता है।
- समय हमेशा एक दिशा में चलता है इसलिए थीटा हमेशा एक पॉजिटिव संख्या होती है।
- ऑप्शन बेचने वाले के लिए थीटा सबसे फायदेमंद ग्रीक होता है।
- जब आप सीरीज की शुरुआत में एक नेकेड ऑप्शन – naked options को शॉर्ट करते हैं तो एक बड़ी रकम टाइम वैल्यू के तौर पर पा सकते हैं लेकिन समय की वजह से प्रीमियम में गिरावट कम होती है।
- जब आप एक्सपायरी के करीब जाकर ऑप्शन को शॉर्ट करते हैं तो प्रीमियम कम होता है क्योंकि समय वैल्यू कम होती है लेकिन प्रीमियम में गिरावट की रफ्तार तेज रहती है।





Agar option ka theta 0.75 hai to uski vajah se 1 hrs..or 1 minutes me price me kya farak padega vo kaise PTA laga skte hai
Koi farak nahi padta.
Thita 1 day ko dikhata ha over night ko.
Ha par 1 minit me vega jarur effect krega
Which option has highest theta otm itm atm. Please reply
ITMs have. But the rate at which theta decay happens is with OTMs.
कुलसुम जी / जिरोधा टीम
आपने ये जो पूरा कांसेप्ट बनाया है यकीन मानिए ये बहुत ही शानदार है।
बस में एक चीज नही समझ पाया की इन सभी के इंग्लिश वीडियो है पर हिंदी विडियो नही क्या आपने सोचा की हिंदी में बहुत से दर्शक है जो वीडियो के द्वारा अच्छा ज्ञान लेना चाहते है वो भी सही तरीके से तो इन सभी को हिंदी विडियो में भी बनाया जाए
हिंदी में भी वीडियोस जल्द ही उपलब्ध होंगे। 🙂
कुलसुम जी / जिरोधा टीम
आपने ये जो पूरा कांसेप्ट बनाया है यकीन मानिए ये बहुत ही शानदार है।
बस में एक चीज नही समझ पाया की इन सभी के इंग्लिश वीडियो है पर हिंदी विडियो नही क्या आपने सोचा की हिंदी में बहुत से दर्शक है जो वीडियो के द्वारा अच्छा ज्ञान लेना चाहते है वो भी सही तरीके से तो इन सभी को हिंदी विडियो में भी बनाया जाए
दिया हुआ थीटा value percent मे होता है, या पूरे दिन में होने वाली decay value होती है l
Time value 9,15 se 3:30 k bichme kaise Kam hoti Hain
हमने पूरा कांसेप्ट इसी अध्याय में समझाया है कृपया इसको पूरा पढ़ें।
Kisi share ka theeta kitna hai kaise or kaha par check karen
thank you zerodha team
Happy learning 🙂
Agr main put sell krta hun to aur premium 50 Rs hai. Next day 45 hua fir next day 40 hua and fir maine exit kr liya apni position to mujhe kya earning hogi.. suppose lot size 100.
Basically m janna chahta hu mujhe daily Paise milenge.
50×100=5000
45×100=4500
40×100=4000
Total 13500
Is it correct?
लेकिन याद रखिए कि प्रीमियम में में गिरावट की गति कम होती है।
इसमे में एक ही बार आना चाहिए।
सूचित करने के लिए धन्यवाद हम इसको सही करदेंगे।
प्रीमियम = इंट्रिन्सिक वैल्यू + टाइम वैल्यू
isme Time Value kaise nikalte hain.
इसका फार्मूला भी उसी अध्याय में बताया गया है।
Dear Mr. Rangappa,
Its really very nice explanation for all the options… I was searching for similar knowledge since so long. God bless you always.
Thanks
Thank you, Yunus and Happy Learning 🙂
बहुत बहुत धन्यवाद
जब हम एक्सपायरी की तरह बढ़ते हैं
सर यहाँ तरफ़ होना चाहिए
हमने इसे सही करदिया है, धन्याद।