6.1 – संक्षिप्त विवरण

यह अध्याय हमारे मुख्य विषय से थोड़ा हटकर है। 

पिछले अध्याय में हमने पोर्टफोलियो वैरियंस के बारे में चर्चा की थी। अब हमने इतनी मेहनत करके पोर्टफोलियो वैरियंस निकाला और अगर उसका इस्तेमाल ना करें तो फिर कोई फायदा नहीं। इसलिए अगले 2 अध्याय में हम यही काम करेंगे। 

अगले 2 अध्यायों में हम कोशिश करेंगे कि 

• इक्विटी कर्व (curve) पर चर्चा करें और पोर्टफोलियो वैरियंस निकालने का एक दूसरा रास्ता देखें 
• पोर्टफोलियो का 1 साल का एक्सपेक्टेड रिटर्न निकालें 
• पोर्टफोलियो में इस तरह के बदलाव करें जिससे रिटर्न अधिक हो जाए और वैरियंस कम हो जाए 

ध्यान दीजिए कि ये अध्याय पिछले अध्याय में की गई चर्चा पर आधारित है। इसलिए अगर आप इस अध्याय को बिना पीछे की चीजों को जाने समझे पढ़ेंगे तो कोई फायदा नहीं होगा। मेरी सलाह है कि अगर आपने अब तक वह अध्याय नहीं पढ़े हैं तो पहले जाकर उनको पढ़ लें।

6.2 – इक्विटी कर्व

हम यहां पर अपने पांच स्टॉक के पोर्टफोलियो के लिए एक इक्विटी कर्व बनाने की कोशिश करेंगे। अगर संक्षेप में कहें तो, एक आम इक्विटी कर्व आपको 100 के स्केल पर पोर्टफोलियो का परफॉर्मेंस दिखाता है। मतलब यह आपको बताता है कि अगर आपने अपने पोर्टफोलियो में ₹100 का निवेश किया है तो एक निश्चित समय के बाद उससे कितनी कमाई हुई है यानी आपका पोर्टफोलियो कैसा परफॉर्मेंस दिखा रहा है। आप इस कर्व का इस्तेमाल ये देखने के लिए भी कर सकते हैं कि आपका पोर्टफोलियो अपने बेंचमार्क यानी Nifty50 या BSE Sensex के मुकाबले किस तरह का प्रदर्शन कर रहा है। 

इक्विटी कर्व में से और भी कई तरह की जानकारी निकाली जा सकती है जो आपको पोर्टफोलियो के बारे में काफी कुछ बता सकती है। लेकिन उस पर चर्चा बाद में करेंगे। 

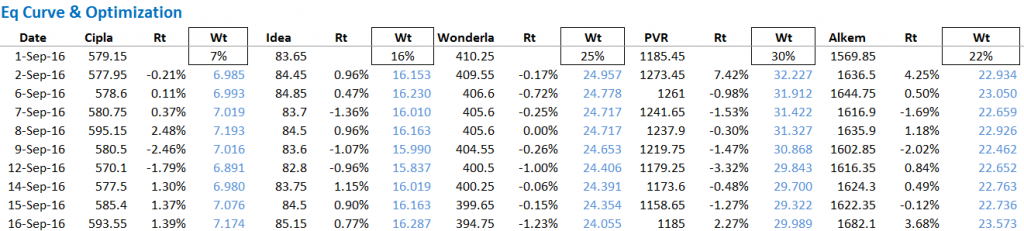
पहले अपने 5 स्टॉक के पोर्टफोलियो के लिए इक्विटी कर्व बनाते हैं। आपको याद होगा कि हमने पिछले अध्याय में ये पांच स्टॉक चुने थे और उनको अलग अलग वजन दिया था। नीचे के चित्र में उन पांचों स्टॉक के नाम और पोर्टफोलियो में उनका कितना वजन है वह दिखाया गया है-

स्टॉक का नाम	निवेश का वजन
सिप्ला	7%
आइडिया सेलुलर लि	16%
वंडरला	25%
PVR	30%
एल्केम	22%

तो, यह निवेश का वजन यानी इन्वेस्टमेंट वेट होता क्या है? वास्तव में यह बताता है कि आप के कुल निवेश का कितना प्रतिशत किसी स्टॉक में लगा है। उदाहरण के लिए ₹100,000 में से ₹7,000 सिप्ला में जाएंगे और ₹22,000 एल्केम लैब में निवेश होंगे। और इसी तरह बाकियों में भी। 

इक्विटी कर्व बनाने के लिए आम तरीका यह है कि पोर्टफोलियो को ₹100 के हिसाब से देखा जाए। इससे हमें यह समझने में आसानी होती है कि अगर ₹100 इस पोर्टफोलियो में निवेश किए गए हैं तो वह रकम इस निश्चित अवधि में कहां तक पहुंची है। हमने पिछले अध्याय में जिस एक्सेल शीट का इस्तेमाल किया था, मैंने उसी में पोर्टफोलियो को 100 के हिसाब से दिखा दिया है। नीचे के चित्र पर नजर डालिए- 

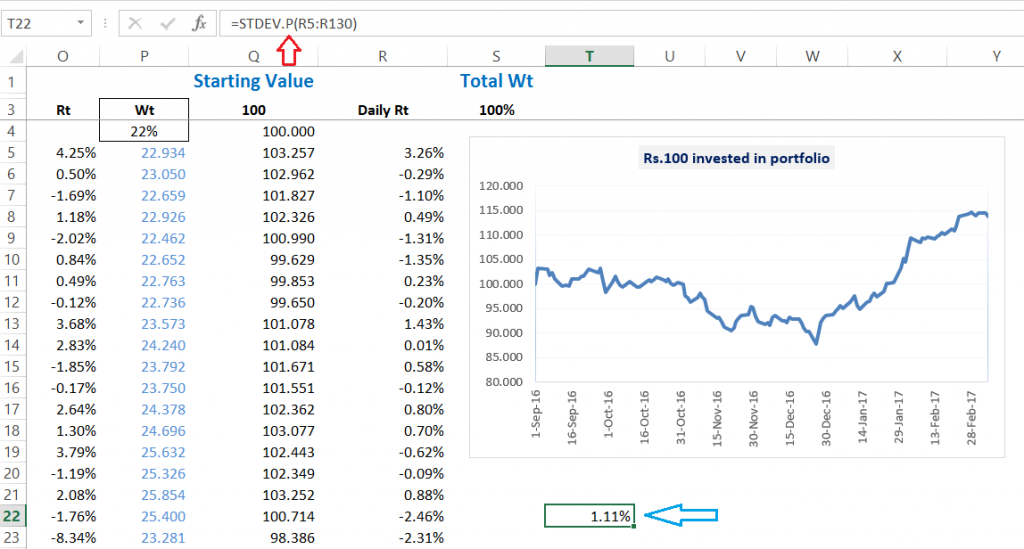
आपको यहां दिखेगा कि मैंने डेली रिटर्न के कॉलम (Column) के बगल में एक नया कॉलम डाला है और उसमें उस स्टॉक का पोर्टफोलियो में वजन कितना है यह दिखाया है। इसी तरह, अंत में आपको दो और कॉलम दिखेंगे जो यह बता रहे हैं कि शुरुआती निवेश ₹100 का है और कुल वजन 100% है। 

शुरुआती निवेश उस रकम को दिखाता है कि जितने पैसे से हम निवेश की शुरुआत कर रहे हैं। मैंने इसको ₹100 रखा है। इसका मतलब है कि ₹100 में से ₹7 सिप्ला में निवेश हो रहे हैं ₹16 आईडिया में निवेश हो रहे हैं, ₹25 वांडरला में निवेश हो रहे हैं और इसी तरह से बाकी निवेश भी बांटा गया है। 

अब मैं अगर हर निवेश के वजन को एक साथ जोड़ लूं तो यह 100% होना चाहिए, जो हमें यह बताता है कि ₹100 का 100% निवेशित है। 

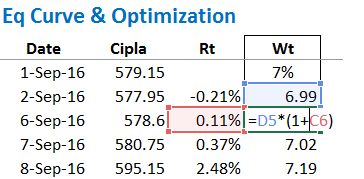
अब हमें यह देखना है कि हर स्टॉक में किया गया निवेश किस तरह का प्रदर्शन दिखा रहा है। इसको ज्यादा अच्छे से समझने के लिए सबसे पहले सिप्ला का उदाहरण लेते हैं। सिप्ला का पोर्टफोलियो में वजन 7% है इसका मतलब है कि ₹100 में से ₹7 से सिप्ला में निवेश किए गए हैं। सिप्ला के स्टॉक की कीमत में हर दिन होने वाले बदलाव की वजह से यह ₹7 या तो बढ़ेंगे या घटेंगे। यहां पर याद रखने वाली बात यह है कि अगर पहले दिन हमारे ₹7 बढ़कर  ₹7.50 हो जाते हैं तो अगले दिन हमारा शुरुआती निवेश ₹7.50 रहेगा ₹7 नहीं। मैंने एक एक्सेल में इसको बनाया है- 

1 सितंबर को सिप्ला की कीमत ₹579.15 थी। इस दिन हमने इस स्टॉक में ₹7 निवेश करने का फैसला किया। मुझे पता है कि तकनीकी रूप से यह संभव नहीं है लेकिन उदाहरण के लिए इसे हम मान लेते हैं। 1 सितंबर को हमने ₹7 का निवेश किया। 2 सितंबर को सिप्ला 577.5 रुपए पर बंद हुआ मतलब -0.21% नीचे। इसका मतलब यह हुआ कि अपने ₹7 के निवेश पर हमने 0.21% का नुकसान उठाया और अब हमारे निवेश की कीमत बची ₹6.985, 6 सितंबर को सिप्ला 0.11% बढ़ा और ₹578.6 पर बंद हुआ इस तरह हमारा ₹6.985 भी 0.11% बढ़ा और ₹6.993 हो गया। और यह इसी तरीके से आगे भी चलता रहेगा 

मैंने पोर्टफोलियो के सभी स्टॉक के लिए ये जोड़ घटाव किया है और ये रहा उसका टेबल –

मैंने हर स्टॉक में निवेश की गई रकम के मुकाबले कीमत में हर दिन होने वाले बदलाव को निकाला है और उसे नीले रंग से हाईलाइट किया है।ध्यान दीजिए, मैंने ₹100 को पांच अलग-अलग स्टॉक में बांटा है और उनको स्टॉक के वजन के हिसाब से निवेश कर दिया है। अब अगर मैं हर स्टॉक की कीमत में हर दिन के बदलाव को देखूं तो मुझे यह पता चल जाएगा कि मेरे ₹100 के कुल निवेश में हर दिन किस तरह का बदलाव हो रहा है। इस तरीके से मुझे यह पता चल जाएगा कि मेरा पोर्टफोलियो किस तरह का प्रदर्शन कर रहा है। यह गणना करके देखते हैं कि मेरा ₹100 जो कि 5 स्टॉक में लगा है वह हर दिन किस तरह से चल रहा है। 

इन सब अलग-अलग संख्याओं को जोड़कर देखें तो मुझे इनके कीमत में हर दिन होने वाले बदलाव का एक टाइम सीरीज मिल जाएगा 

अब अगर मैं इसको एक ग्राफ पर डाल दूं तो यह मुझे इक्विटी कर्व बन कर मिल जाएगा। मतलब कि पोर्टफोलियो के हर दिन की नॉर्मलाइज्ड कीमत का टाइम सीरीज डेटा मिल जाएगा। मैं नॉर्मलाइज्ड कीमत इसलिए कह रहा हूं क्योंकि मैंने इसे ₹100 के लिए बनाया है।

तो यह रहा हमारे पोर्टफोलियो का इक्विटी कर्व –

तो इतना आसान है इसको बनाना। पोर्टफोलियो का परफॉरमेंस देखने के लिए इस इक्विटी कर्व का काफी इस्तेमाल होता है। ये पता चलता है कि पोर्टफोलियो कितना रिटर्न दे रहा है। इस उदाहरण में हमने ₹100 से निवेश शुरू किया और 6 महीने बाद उसकी वैल्यू 113.84 हो गयी। नीचे के चित्र को देखिए

तो सीधे सादे तरीके से मुझे पता है कि मेरा पोर्टफोलियो 6 महीने की इस अवधि में 13.8% की कमाई कर चुका है।

6.3 – पूरा पोर्टफोलियो एक यूनिट

अब एक नई चीज पर नजर डालते हैं। पिछले अध्याय में हमने पोर्टफोलियो वैरियंस निकाला था। इसे निकालने के लिए हमने हर स्टॉक का स्टैन्डर्ड डेविएशन निकाला था। जैसा कि आपको पता है कि स्टैन्डर्ड डेविएशन हमें उस स्टॉक की वोलैटिलिटी को बताता है और ये और कुछ नहीं बस उस स्टॉक से जुड़ा हुआ रिस्क है। 

स्टैन्डर्ड डेविएशन निकालने के लिए हमने स्टॉक के डेली रिटर्न पर एक्सेल में ‘=STDEV()’ फंक्शन का इस्तेमाल किया था। लेकिन, अब तो हमें हमारे पोर्टफोलियो की हर दिन की कीमत या वैल्यू पता है (भले ही वो 100 के हिसाब से नॉर्मलाइज्ड है।) 

तो अगर हम यह मान लें कि हमारा पोर्टफोलियो एक स्टॉक है और हम इसका हर दिन का रिटर्न निकाल लें, जैसे कि हमने पिछले अध्याय में हर स्टॉक का अलग-अलग डेली रिटर्न निकाला था। अगर मैं यहां पर  ‘=STDEV()’ फंक्शन का इस्तेमाल पोर्टफोलियो का डेली रिटर्न निकालने के लिए करूं तो? तो इससे जो स्टैन्डर्ड डेविएशन हमें मिलेगा वह पोर्टफोलियो का स्टैन्डर्ड डेविएशन होगा जो कि वास्तव में पोर्टफोलियो का वैरियंस होगा यानी पोर्टफोलियो के रिस्क को बता रहा होगा। 

तो आपको समझ में आ गया मैं क्या कर रहा हूं, जी हां हम पोर्टफोलियो वैरियंस निकालने की कोशिश कर रहे हैं, लेकिन एक दूसरे तरीके से। 

आपको यह बात अच्छे से समझ में आ जाए इसलिए हम ने पिछले अध्याय में जो पोर्टफोलियो वैरियंस निकाला था उसे यहां नीचे दिखा रहा हूं-

इस पोर्टफोलियो वैरियंस निकालने के लिए हमने मैट्रिक्स मल्टीप्लिकेशन किया था और कोरिलेशन मैट्रिक्स तकनीक का इस्तेमाल किया था। 

लेकिन अब हम पोर्टफोलियो को एक यूनिट की तरह देखेंगे और स्टॉक की तरह से नॉर्मलाइज्ड वैल्यू वाले इस पोर्टफोलियो का हर दिन का रिटर्न निकालेंगे। पोर्टफोलियो के हर दिन के रिटर्न का स्टैन्डर्ड डेविएशन हमें जो संख्या बताएगा वह पोर्टफोलियो वैरियंस के आसपास होनी चाहिए जिसे हमने पहले निकाला हुआ है।  

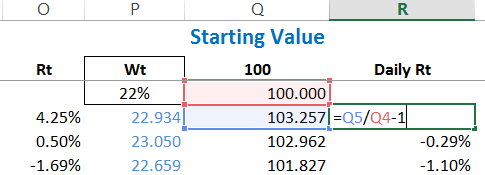
मैंने अपने नॉर्मलाइज्ड वैल्यू वाले इस पोर्टफोलियो के वैल्यू के बगल में एक नया कॉलम बनाया है और वहां पोर्टफोलियो का हर दिन का रिटर्न निकाला है। 

जब हमारा रिटर्न निकल जाएगा तो मैं स्टैन्डर्ड डेविएशन फंक्शन का इस्तेमाल करूंगा जिससे मुझे पहले निकाले गए पोर्टफोलियो वैरियंस के आसपास की कोई संख्या/वैल्यू मिलनी चाहिए

तो आप जैसा देख सकते हैं कि STDEV भी फंक्शन से हमें वही संख्या मिली है। 

इस अध्याय में इस्तेमाल किए गए एक्सेल शीट को आप यहां से डाउनलोड- download  कर सकते हैं अगले अध्याय में हम पोर्टफोलियो वैरियंस का इस्तेमाल करके एक्सपेक्टेड रिटर्न निकालेंगे और पोर्टफोलियो को सुधारेंगे भी।

आपके लिए अभ्यास- हमने हर स्टॉक को एक वजन दिया है, आपको बस ये करना है कि उस वजन को बदल कर देखिए कि कुल रिटर्न पर किस तरह का असर पड़ता है। अपना नतीजा हमारे साथ शेयर कीजिए कमेंट बॉक्स में।

 इस अध्याय की मुख्य बातें 

1. किसी पोर्टफोलियो का प्रदर्शन देखने का एक आम तरीका है – इक्विटी कर्व को देखना 
2. इक्विटी कर्व बनाने के लिए आमतौर पर जो तरीका इस्तेमाल किया जाता है उसमें शुरुआती निवेश की कीमत को 100 रखा जाता है 
3. हम पोर्टफोलियो के हर स्टॉक में निवेश को अलग-अलग वजन देते हैं 
4. हमें हर निवेश की कीमत में हर दिन होने वाले बदलाव को निकालना होता है 
5. हर स्टॉक में हर दिन होने वाले इस बदलाव का जोड़ ही उस पोर्टफोलियो में होने वाला बदलाव होता है 
6. हर दिन के इस बदलाव को अगर एक ग्राफ पर देखा जाए तो यह पोर्टफोलियो का इक्विटी कर्व हो जाता है 
7. हम पोर्टफोलियो को एक स्टॉक की तरह देखकर उसका स्टैन्डर्ड डेविएशन निकाल सकते हैं 
8. पोर्टफोलियो का स्टैन्डर्ड डेविएशन ही पोर्टफोलियो वैरियंस भी बताता है