फिबोनाची रीट्रेसमेंट्स काफी रोचक विषय है। फिबोनाची रीट्रेसमेंट्स की अवधारणा को पूरी तरह से समझने और सराहने के लिए आपको फिबोनाची श्रृंखला को समझना होगा। कुछ दावों के मुताबिक फिबोनाची श्रृंखला की उत्पत्ति प्राचीन भारतीय गणित लिपियों में 200 ईसा पूर्व में हुई थी। लेकिन इसके मौजूदा स्वरूप की खोज 12वीं शताब्दी में इटली के पीसा शहर के गणितज्ञ लियोनार्डो पिसानो बोगोलो ने की थी। बोगोलो के दोस्त उसे फिबोनाची बुलाते थे और फिबोनाची ने ही फिबोनाची संख्या की खोज की।
फिबोनाची श्रृंखला शून्य से शुरू होने वाली संख्याओं का एक क्रम है, जो इस तरह से व्यवस्थित हैं कि श्रृंखला में किसी भी संख्या का मूल्य पिछले दो संख्याओं का जोड़ है।
फिबोनाची श्रृंखला निम्नानुसार है:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610…
निम्नलिखित पर ध्यान दें:
233 = 144 + 89
144 = 89 + 55
89 = 55 +34
मतलब पिछली दो संख्याओं के जोड़ से अगली संख्या बनती है और ये ऐसे ही श्रृंखला अनंत तक चलती है। फिबोनाची श्रृंखला के कुछ दिलचस्प गुण हैं।
श्रृंखला में किसी भी संख्या को पिछले संख्या से विभाजित करें तो अनुपात हमेशा लगभग 1.618 होगा।
उदाहरण के लिए:
610/377 = 1.618
377/233 = 1.618
233/144 = 1.618
1.618 के अनुपात को गोल्डन अनुपात (Golden Ratio) भी कहा जाता है, इसे फाई (Phi) भी कहा जाता है। फिबोनाची संख्याओं के इस गुण का संबंध हमारी प्रकृति से भी है। गोल्डन अनुपात को आप मानव चेहरे, फूलों की पंखुड़ियों, जानवरों के शरीर, फल, सब्जियां से लेकर पत्थरों और अंतरिक्ष में भी देख सकते हैं। अभी इस पर चर्चा नहीं करेंगे क्योंकिऐसा करने से हम मुख्य विषय से हट जाएंगे। लेकन इसमें रुचि रखने वाले लोग इंटरनेट पर गोल्डन अनुपात के उदाहरणों को खोज सकते हैं। आपको काफी आश्चर्यजनक जानकारियां मिलेंगी। गोल्डन अनुपात के अलावा फिबोनाची श्रृंखला का एक और गुण है, जब इस श्रृंखला की कोई संख्या, श्रृंखला में अपने तुरंत बाद आने वाली संख्या से विभाजित होती है, तो ये अनुपात भी स्थिर ही रहता है।
उदाहरण के लिए:
89/144 = 0.618
144/233 = 0.618
377/610 = 0.618
यहाँ पर, ध्यान रखें कि 0.618, जब प्रतिशत में व्यक्त किया जाता है 61.8% है।
इसी तरह की स्थिरता तब भी पाई जाती है जब फिबोनाची श्रृंखला में कोई भी संख्या अपने से दो स्थान बाद आने वाली संख्या से विभाजित हो।
उदाहरण के लिए:
13/34 = 0.382
21/55 = 0.382
34/89 = 0.382
0.382 प्रतिशत के संदर्भ में 38.2% है।
इसी तरह के परिणाम आप तब भी देखेंगे जब फिबोनाची श्रृंखला की एक संख्या को उसके 3 जगह बाद आने वाली संख्या से विभाजित किया जाता है।
उदाहरण के लिए:
13/55 = 0.236
21/89 = 0.236
34/144 = 0.236
55/233 = 0.236
0.236 प्रतिशत के संदर्भ में 23.6% है।
16.1 – शेयर बाजारों में उपयोगिता (Relevance to stocks markets)
ऐसा माना जाता है कि फिबोनाची अनुपात यानी 61.8%, 38.2% और 23.6% का स्टॉक चार्ट में उपयोग किया जा सकता है। फिबोनाची विश्लेषण तब लागू किया जा सकता है जब कीमतों में अच्छा खासा उतार या चढ़ाव हो। जब भी स्टॉक तेजी से ऊपर या नीचे की ओर बढ़ता है, तो आमतौर पर यह अपनी अगली चाल से पहले एक स्तर तक वापस लौटता है। उदाहरण के लिए, यदि स्टॉक 50 रुपये से लेकर 100 रुपये तक चला है, तो इससे पहले कि यह Rs.120 तक आगे बढ़ सके इसके Rs.70 तक वापस आने (रीट्रेसमेंट करने) की संभावना होती है।
‘रीट्रेसमेंट लेवल फोरकास्ट – The retracement level forecast’ एक ऐसी तकनीक है जिसके इस्तेमाल से कोई भी पहचान कर सकता है कि किस लेवल तक की रीट्रेसमेंट हो सकता है। ये रीट्रेसमेंट लेवल ही ट्रेडर को मौका देते हैं कि वो ट्रेंड की दिशा को देख कर नए सौदे कर सकें। फिबोनाची अनुपात यानी 61.8%, 38.2% और 23.6% ट्रेडर को रीट्रेसमेंट की संभावित सीमा को पहचानने में मदद करता है। ट्रेडर इन स्तरों का उपयोग ट्रेड के लिए कर सकता है।
नीचे दिए गए चार्ट पर एक नज़र डालें:
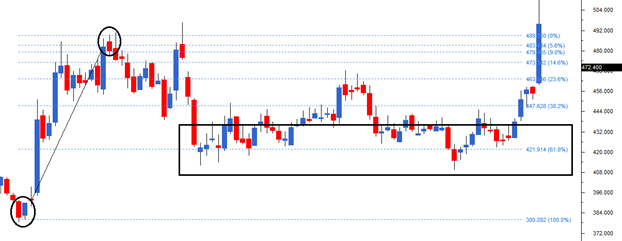
मैंने चार्ट पर दो बिंदुओं को घेरा है, 380 रुपये पर जहां शेयर ने अपनी रैली शुरू की और 489 रुपये पर, जहां शेयर की कीमतें अपनी ऊँचाई पर थीं।
अब मैं 109 (380 – 489) तक की चाल (move) को फिबोनाची अपमूव (Fibonacci Upmove) यानी चढ़ाव के रूप में परिभाषित करूंगा। फिबोनाची रीट्रेसमेंट सिद्धांत के अनुसार, ऊपर चढ़ रहा कोई भी स्टॉक जब करेक्शन में आता है तो वो फिबोनाची अनुपात तक गिर सकता है। उदाहरण के लिए, स्टॉक का पहला करेक्शन 23.6% तक हो सकता है। यदि यह स्टॉक आगे भी करेक्ट होता है, तो 38.2% और 61.8% के स्तर भी दिखा सकता है।
नीचे दिखाए गए उदाहरण में स्टॉक 61.8% तक नीचे आ गया है, जो 421.9 के साथ मेल खाता है, इसके बाद ही यह फिर से रैली शुरू करता है।
हम साधारण गणित का उपयोग करके भी 421 तक पहुंच सकते हैं –
कुल फिबोनाची बढत = 109
फिबोनाची की 61.8% चाल = 61.8% * 109 = 67.36
रिट्रेसमेंट @ 61.8% = 489- 67.36 = 421.6
इसी तरह, हम 38.2% और अन्य अनुपातों के लिए गणना कर सकते हैं। हालाँकि हमें ऐसा करने की आवश्यकता नहीं है क्योंकि हमारे लिए ये काम सॉफ़्टवेयर करता है।
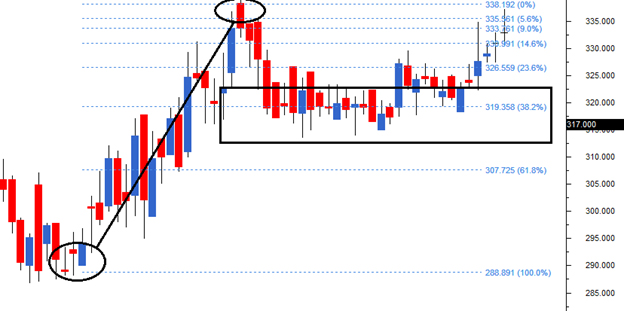
यहां एक और उदाहरण है जहां चार्ट 288 से 338 तक बढ़ा हुआ है। इसलिए 50 प्वाइंट की ये बढत फिबोनाची अपमूव से जुड़ी बढ़त है। स्टॉक ने अपनी चाल को दोबारा से शुरू करने से पहले 38.2% तक यानी 319 तक रीट्रेस किया।
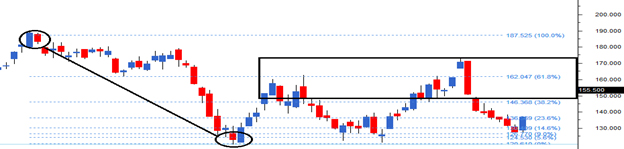
फिबोनाची रीट्रेसमेंट उन शेयरों पर भी लागू किया जा सकता है जो गिर रहे हैं, इसके जरिए हम उस स्तर की पहचान कर सकते हैं जहां से स्टॉक वापस उछल सकता है। नीचे दिए गए चार्ट (DLF Limited) में, शेयर 187 से 120.6 तक गिरा और इस प्रकार फिबोनाची डाउन के रूप में 67 अंक बनते हैं।
नीचे गिरने के बाद, शेयर ने वापस आकर 162 तक उछाल देने का प्रयास किया, जो कि 61.8% फिबोनाची रीट्रेसमेंट स्तर है।
16.2 – फिबोनाची रीट्रेसमेंट का निर्माण (Fibonacci Retracement construction)
जैसा कि अब हम जानते हैं कि फिबोनाची रीट्रेसमेंट किसी चार्ट के उन बदलावों को दिखाते हैं जो ट्रेंड के खिलाफ जाते हैं। फिबोनाची रीट्रेसमेंट का उपयोग करने के लिए हमें पहले फिबोनाची चाल 100% मूल्य पता करना चाहिए। चाल चाहे ऊपर की रैली में हो या नीचे की रैली में। चाल के 100% को पता करने के लिए, हमें चार्ट पर सबसे हाल के हाई और लो को चुनने की जरूरत पड़ेगी। इनकी पहचान हो जाने के बाद, हम फिबोनाची रीट्रेसमेंट टूल का उपयोग करके इन्हें कनेक्ट करते हैं। यह टूल Zerodha के Pi सहित टेक्निकल एनालिसिस के कई सॉफ्टवेयर पैकेजों में उपलब्ध है।
अब इसके उपयोग को समझते हैं:
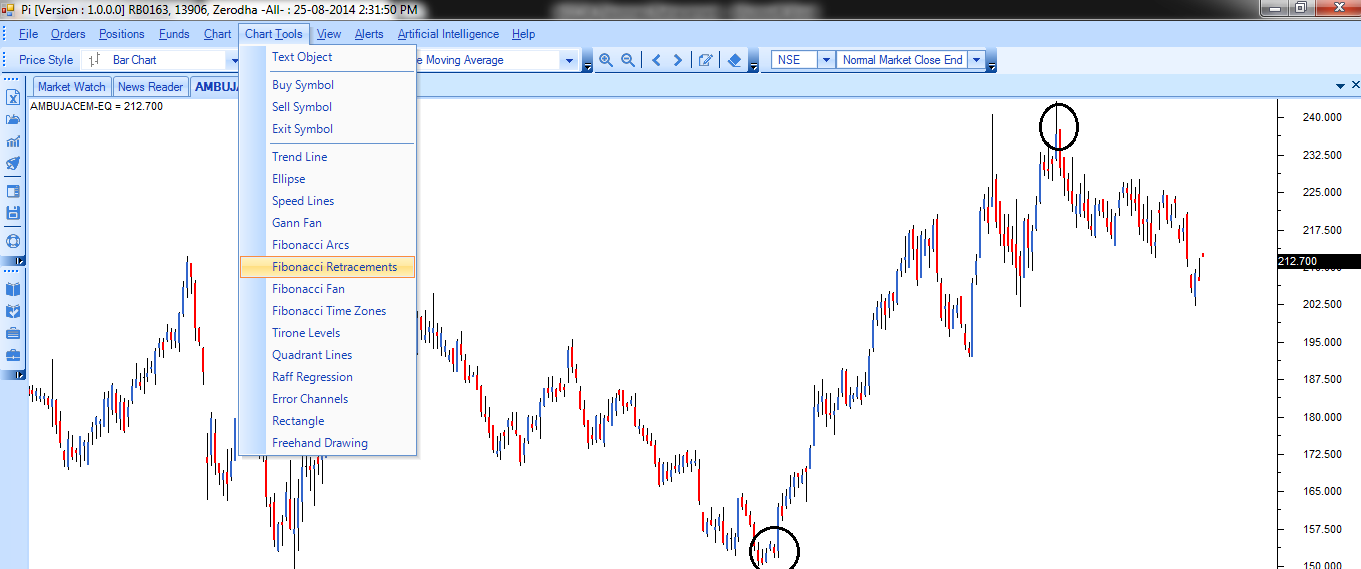
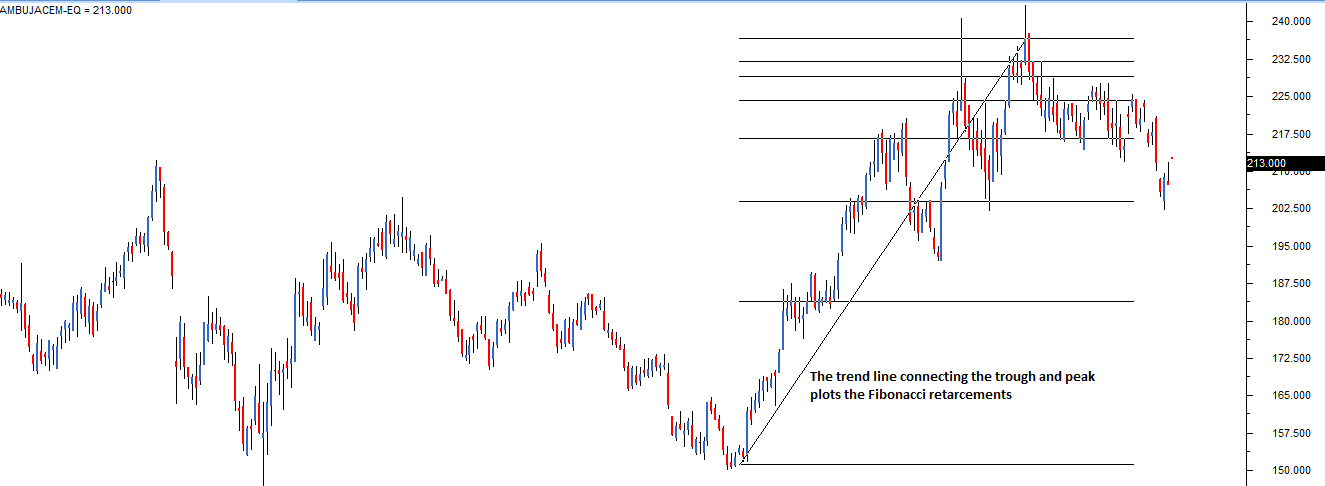
चरण 1) सबसे नए हाई और लो की पहचान करें। इस मामले में लो 150 पर है और हाई 240 पर है। यानी यहाँ 90 प्वाइंट की चाल है। इसका मतलब 90 प्वाइंट ही यहाँ 100% है।
चरण 2) चार्ट के टूल में से फिबोनाची रीट्रेसमेंट टूल को चुनें।
चरण 3) अब फिबोनाची रीट्रेसमेंट टूल के जरिए लो और हाई को आपस में जोड़ें।
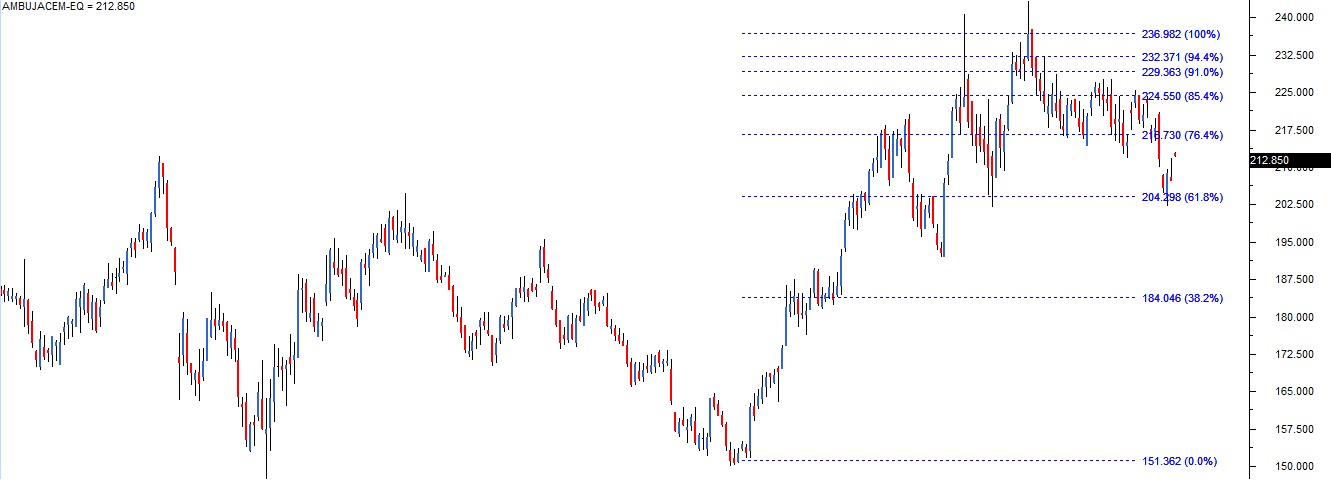
चार्ट टूल से फिबोनाची रीट्रेसमेंट टूल को चुनने के बाद ट्रेडर को पहले लो पर क्लिक करना होगा और बिना क्लिक किए उस लाइन को हाई तक खींचना होगा। इसे करने के साथ ही साथ फिबोनाची रीट्रेसमेंट स्तर चार्ट पर प्लॉट होने लगता है। जैसे ही आप सॉफ़्टवेयर में लो और हाई दोनों को चुन लेते हैं, वैसे ही रीट्रेसमेंट पहचानने की प्रक्रिया पूरी हो जाती है। दोनों बिंदुओं को चुनने के बाद चार्ट ऐसा दिखता है।
अब आप देख सकते हैं कि चार्ट पर फिबोनाची रीट्रेसमेंट स्तर बन कर दिख रहा है। इस जानकारी का उपयोग करके आप बाजार में पोजीशन बना सकते हैं।
16.3 – आपको फिबोनाची रीट्रेसमेंट स्तरों का उपयोग कैसे करना चाहिए? (How should you use Fibonacci retracement levels)
एक ऐसी स्थिति के बारे में सोचें जहां आप एक खास स्टॉक खरीदना चाहते थे लेकिन उसमें बहुत ज्यादा तेजी आने के कारण आप उसे नहीं खरीद पाए। ऐसी स्थिति में सबसे समझदारी का काम होगा स्टॉक में रीट्रेसमेंट के लिए इंतजार करना। वो स्टॉक फिबोनाची रीट्रेसमेंट स्तर यानी 61.8%, 38.2% और 23.6% तक गिर (रीट्रेस) सकता है।
फिबोनाची रीट्रेसमेंट स्तर को चार्ट पर पहचान कर ट्रेडर इन स्तरों पर में स्टॉक में प्रवेश करने के अवसर के लिए तैयार रह सकता है। लेकिन, याद रखें कि किसी भी दूसरे इंडिकेटर की तरह ही इसका इस्तेमाल भी पुष्टि के लिए ही करना चाहिए।
मतलब ये कि चेकलिस्ट की बाकी शर्तों के पूरा होने के बाद ही मैं शेयर खरीदूंगा सिर्फ फिबोनाची रीट्रेसमेंट के आधार पर नहीं। दूसरे शब्दों में, स्टॉक तो खरीदने के लिए मेरा विश्वास अधिक होगा अगर:
- एक पहचानने योग्य कैंडलस्टिक पैटर्न का बन रहा है।
- स्टॉपलॉस और S&R स्तर मेल खा रहे हैं।
- वॉल्यूम औसत से ऊपर हैं।
ऊपर के बिदुओं के साथ साथ अगर स्टॉपलॉस भी फिबोनाची स्तर के साथ मेल खाता है, तो मुझे पता है कि ट्रेड सेटअप सभी शर्तो को पूरा कर रहा है और इससे मेरा भरोसा बढेगा और मैं खरीदने के लिए मजबूती से जाऊंगा। याद रखिए कि ट्रेंड और रिवर्सल का अध्ययन करते हुए हम जितने ज्यादा तरीकों से इनकी पुष्टि करते हैं, संकेत उतना ही भरोसेमंद होता है। शॉर्ट ट्रेड या लांग, दोनों के लिए।
इस अध्याय की मुख्य बातें
- फिबोनाची रीट्रेसमेंट का आधार फिबोनाची श्रृंखला बनाती है।
- एक फिबोनाची श्रृंखला में कई गणितीय गुण हैं। ये गणितीय गुण प्रकृति के कई पहलुओं में भी दिखते हैं।
- कारोबारी मानते हैं कि स्टॉक चार्ट में फिबोनाची श्रृंखला का उपयोग है क्योंकि यह संभावित रीट्रेसमेंट स्तरों की पहचान करता है।
- फिबोनाची रीट्रेसमेंट स्तर (61.8%, 38.2%, और 23.6%) हैं, एक तेजी से चढ़ता शेयर अपने ट्रेंड की मूल दिशा में फिर से चलने से पहले संभवतः इन स्तरों तक वापस गिर सकता है।
- फिबोनाची रीट्रेसमेंट स्तर पर ट्रेडर एक नया ट्रेड शुरू करने पर विचार कर सकता है। हालांकि, व्यापार शुरू करने से पहले उसे चेकलिस्ट में दिए गए अन्य बिंदुओं की भी पुष्टि करनी चाहिए।





Sir, Fibonacci ke sabi chapters hindi m publish kare.
Bahut achha , aapne hame sikhaya hai.
psychology wale module ko bhi hindi me translate kar dijiye sir
हम आपके फीडबैक पर ज़रूर नज़र डालेंगे।
Kya yeh indicator kite app mai v hai?
अब इन सभी की pdf भी उपलब्ध करवा दे। और varsity की application पर भी हिंदी मे module और exam उपलब्ध करवा दीजिये।
बहुत ही अच्छा प्रयास।
जल्द ही उपलब्ध कराया जायेगा।
Very helpful ☺️👍
Thank you 🙂
Dear Team,
Fibonacci Retracement indicator is not available in zerodha mobile app at play store. What to do?
Hi, you could check our website and read this Kite manual https://kite.trade/docs/kite/ for features offered, if you want to suggest some other features please write on Zerodha\’s support channel.
Kya Febonachi retreshment chart Kite application me dekha ja sakta he?
जी हाँ 🙂
what time period required for use fibonachi and can we use this for one day candle to check long term investment purpose?
Hi, kya fibonacci ko apne zerodha chart m use kar saktey hain
जी हाँ कर सकते हैं।
What is difference between fibonachi retracement and fibo default and which time period we shoud use this both tool and how
Please explain this in hindi bcz my english is little week
Sir baki ke module me itna time kese LG rha h trasralate me
Hi पंकज, हम बाकी मॉड्यूल्स को भी जल्द ही ट्रांसलेट करेंगे|
thanks sir next chapter bhi hindi me translate kr do sir